leetcode之820. 单词的压缩编码 | python极简实现字典树
ManWingloeng 人气:0
# 题目
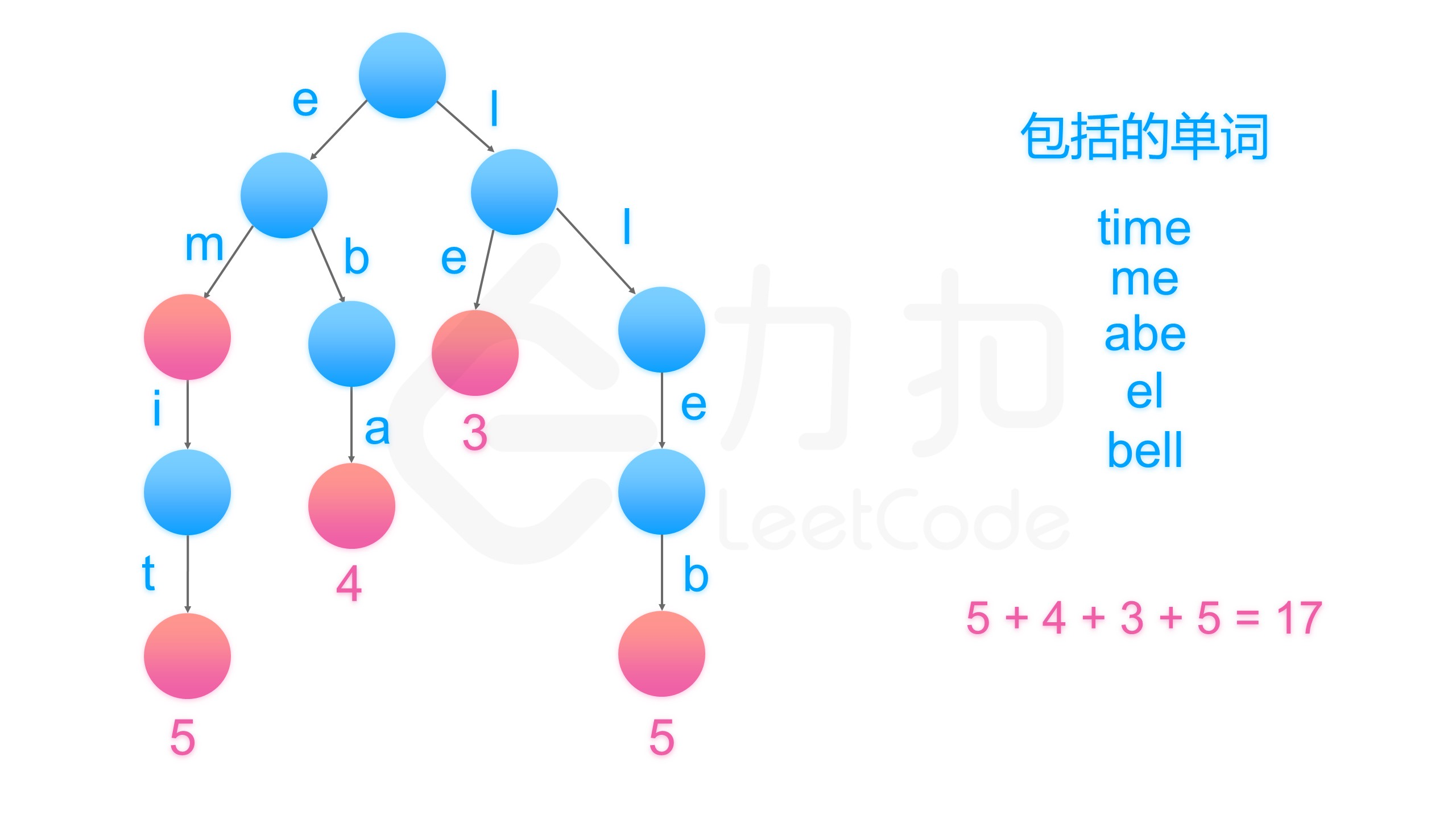
给定一个单词列表,我们将这个列表编码成一个索引字符串 S 与一个索引列表 A。
例如,如果这个列表是 ["time", "me", "bell"],我们就可以将其表示为 S = "time#bell#" 和 indexes = [0, 2, 5]。
对于每一个索引,我们可以通过从字符串 S 中索引的位置开始读取字符串,直到 "#" 结束,来恢复我们之前的单词列表。
那么成功对给定单词列表进行编码的最小字符串长度是多少呢?
```
示例:
输入: words = ["time", "me", "bell"]
输出: 10
说明: S = "time#bell#" , indexes = [0, 2, 5] 。
```
提示:
```
1 <= words.length <= 2000
1 <= words[i].length <= 7
每个单词都是小写字母 。
```
https://leetcode-cn.com/problems/short-encoding-of-words
今天leetcode的每日一题的官方题解的python解法惊艳到我了,代码十分Pythonic,正好我也不太熟悉字典树和reduce的用法,学了一下:
简单的来说就是:一句话实现字典树,一句话完成建树过程。
```python
class Solution:
def minimumLengthEncoding(self, words: List[str]) -> int:
words = list(set(words)) #remove duplicates
#Trie is a nested dictionary with nodes created
# when fetched entries are missing
Trie = lambda: collections.defaultdict(Trie)
trie = Trie()
#reduce(..., S, trie) is trie[S[0]][S[1]][S[2]][...][S[S.length - 1]]
nodes = [reduce(dict.__getitem__, word[::-1], trie)
for word in words]
#Add word to the answer if it's node has no neighbors
return sum(len(word) + 1
for i, word in enumerate(words)
if len(nodes[i]) == 0)
```
`Trie = lambda: collections.defaultdict(Trie)`这个循环嵌套字典是类似这样的效果{{{{}}}},意思是只要没有key的我们就返回一个空字典。
**其实字典树的本质就是循环嵌套字典。**
`trie[word[-1]][word[-2]].........`是写成这样了`reduce(dict.__getitem__, word[::-1], trie)`
下面给出[@Lucien](https://leetcode-cn.com/u/lucien_z/)在leetcode题解下的[评论解释](https://leetcode-cn.com/problems/short-encoding-of-words/solutionhttps://img.qb5200.com/download-x/dan-ci-de-ya-suo-bian-ma-by-leetcode-solution/316724/)
关于Python字典树方法的解释:
我们需要一棵字典树,把所有word加入这棵树
找到所有叶子的高度和
一步步从最正常的写法走向Pythonic的解。
```python
# 定义字典树中的一个节点
class Node(object):
def __init__(self):
self.children={}
class Solution:
def minimumLengthEncoding(self, words: List[str]) -> int:
words = list(set(words)) #需要去重,否则在之后计算“叶子高度”的时候会重复计算
trie=Node() #这是字典树的根
nodes=[] #这里保存着每个word对应的最后一个节点,比如对于单词time,它保存字母t对应的节点(因为是从后往前找的)
for word in words:
now=trie
for w in reversed(word):
if w in now.children:
now=now.children[w]
else:
now.children[w]=Node()
now=now.children[w]
nodes.append(now)
ans=0
for w,c in zip(words,nodes):
if len(c.children)==0: #没有children,意味着这个节点是个叶子,nodes保存着每个word对应的最后一个节点,当它是一个叶子时,我们就该累加这个word的长度+1,这就是为什么我们在最开始要去重
ans+=len(w)+1
return ans
```
相信以上的解答大家可以看懂,那么就从Node开始简化。原先我们把Node声明为一个类,但这个类中只有一个字典,所以我们不如就直接用一个字典来表示节点,一个空字典以为着这是一个叶子节点,否则字典中的每一个元素都是它的一个孩子,上面的代码可以简化为:
```python
class Solution:
def minimumLengthEncoding(self, words: List[str]) -> int:
words = list(set(words)) #需要去重,否则在之后计算“叶子高度”的时候会重复计算
trie={} #这是字典树的根
nodes=[] #这里保存着每个word对应的最后一个节点,比如对于单词time,它保存字母t对应的节点(因为是从后往前找的)
for word in words:
now=trie
for w in reversed(word):
if w in now:
now=now[w]
else:
now[w]={}
now=now[w]
nodes.append(now)
ans=0
for w,c in zip(words,nodes):
if len(c)==0: #一个空字典,意味着这个节点是个叶子
ans+=len(w)+1
return ans
```
继续简化,我们不想在生成字典树时每次都判断“当前字典有没有这个键”,我们希望,有这个键,就返回它的值,否则返回一个空字典给我。很自然,我们需要用到defaultdict,它默认返回一个字典。但,只是返回一个普通字典吗?比如defaultdict(dict)? 不行,实际上它需要返回一个defaultdict,且这个defaultdict仍旧会递归地返回defaultdict。于是,递归地,我们定义这样一个函数,它返回一个defaultdict类型,且它的默认值是该类型本身。 Trie = lambda: collections.defaultdict(Trie) ,注意,这里的Trie是一个函数,它返回一个defaultdict实例。有了它,我们创建字典树的过程就变成了:
```python
nodes=[]
Trie = lambda: collections.defaultdict(Trie)
trie = Trie()
for word in words:
now=trie
for w in word[::-1]:
now=now[w]
nodes.append(now)
```
更进一步,可以简化为
```python
nodes=[]
Trie = lambda: collections.defaultdict(Trie)
trie = Trie()
for word in words:
nodes.append(trie[word[-1]][word[-2]].........)
```
它就变成了
```python
nodes = [reduce(dict.__getitem__, word[::-1], trie)
for word in words]
```
先不管数组的推导式,单看数组的一项 reduce(dict.__getitem__, word[::-1], trie),reduce三个参数分别为:方法,可循环项,初始值。即它初始值是trie,按照word[::-1]的循环顺序,每次去执行方法dict.__getitem__,且将这个输出作为下次循环的输入,所以它就是trie[word[-1]][word[-2]].........的意思。
最后一步的sum很简单,只要大家明白nodes里存的是什么就很明显了。
另外附上标准的C++写法:
```C++
class TrieNode{
TrieNode* children[26];
public:
int count;
TrieNode() {
for (int i = 0; i < 26; ++i) children[i] = NULL;
count = 0;
}
TrieNode* get(char c) {
if (children[c - 'a'] == NULL) {
children[c - 'a'] = new TrieNode();
count++;
}
return children[c - 'a'];
}
};
class Solution {
public:
int minimumLengthEncoding(vector& words) {
TrieNode* trie = new TrieNode();
unordered_map nodes;
for (int i = 0; i < (int)words.size(); ++i) {
string word = words[i];
TrieNode* cur = trie;
for (int j = word.length() - 1; j >= 0; --j)
cur = cur->get(word[j]);
nodes[cur] = i;
}
int ans = 0;
for (auto& [node, idx] : nodes) {
if (node->count == 0) {
ans += words[idx].length() + 1;
}
}
return ans;
}
};
```
加载全部内容