看了数据挖掘的异常检测部分，写一点笔记。

1.0  概述

什么是数据挖掘：数据挖掘

什么是异常检测：异常检测

　　异常检测的目标是发现与大部分其他对象不同的对象。通常，异常对象被称为离群点，因为在数据的散布图中，他们远离其他数据点。异常检测也称为偏差检测、例外挖掘。

　　异常检测的方法各种各样，所有这些的思想都是：异常的数据对象是不寻常的，或者在某些方面与其他对象不一致。

1.1  异常的成因

1. 数据来源于不同的类
   
2. 自然变异
3. 数据测量和收集误差

1.2  异常检测方法

1. 基于模型的技术
　　首先建立一个模型，异常是那些不能完美匹配的对象。例如，数据分布模型可以通过估计概率分布的参数来创建。如果一个对象不能很好地同该模型拟合，即如果它很可能不服从该分布，则它是一个异常。

2. 基于近邻度的技术
　　可以在对象之间定义邻近性度量，许多异常检测方法都基于邻近度。异常对象是那些远离大部分其他对象的对象。当数据用二维或三维散布图显示，可以从视觉上检测出基于距离的离群点。

3. 基于密度的技术
　　对象的密度估计可以相对直接地计算，特别是当对象之间存在近邻性度量时，低密度区域中的对象相对远离近邻，可能被看做异常。

1.3  类标号的使用

异常检测的三种基本方法：

1. 非监督的
2. 监督的
3. 半监督的

三者的主要区别至少对于对于某些数据而言是类标号（异常或正常）可以利用的程度。

1. 监督的异常检测
　　要求存在异常类和正常类的训练集（注意：可能有多个正常类或者异常类）

2. 非监督的异常检测
　　没有提供类标号。在这种情况下，目标是将一个得分（或标号）赋予每个实例，反映该实例是异常的程度。注意，许多相似的异常可能会导致被标记为正常，或有较低的离群点得分。

3. 半监督的异常检测
　　训练数据包含被标记的正常数据，但是没有关于异常对象的信息。目标是使用有标记的正常对象的信息，对于给定的对象集合，发现异常标号。

1.4  问题

1. 用于定义异常的属性个数
　　对象可以有许多属性，它可能在某些属性上具有异常值，而在其他属性上具有正常值。注意，即使一个对象的所有属性值都不是异常，对象也可能异常。

2. 点的异常程度
　　二元方式报告对象是否异常：要么正常要么不正常。这不能反映某些对象比其他对象更加极端异常的基本事实。需要有某种对象异常程度的评估，这种评估称为异常或离群点得分。

3. 全局观点与局部观点
　　一个对象可能相对于所有对象看上去不正常，但是相对于它的局部近邻并非如此。

4. 一次识别一个与多个异常
　　一次一个：每次识别并删除最异常的实例，重复该过程。一次多个：异常集族一起识别。前者常遇到屏蔽问题，后者可能陷入泥潭。

5. 评估
6. 有效性
　　各种方案的计算开销显著不同。

2.0  统计方法

统计学方法是基于模型的方法，即为数据创建模型，根据对象的拟合程度来评估他们。

定义  离群点：离群点是一个对象，关于数据的概率分布模型，它具有低概率。

问题：

1. 识别数据集的具体分布

2. 使用属性的个数

3. 混合分布

2.1  检测一元正态分布的离群点

高斯分布 N(μ，σ)，第一个参数为均值，第二个为标准差。下图为均值为0，标准差为1的高斯分布的概率密度函数：

 

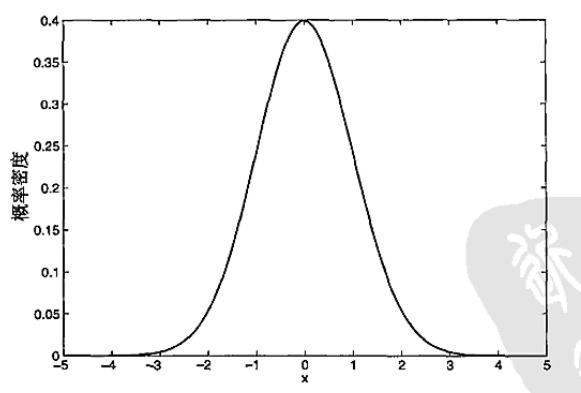
来自N(0,1)分布的对象，出现在尾部的机会很小 

 

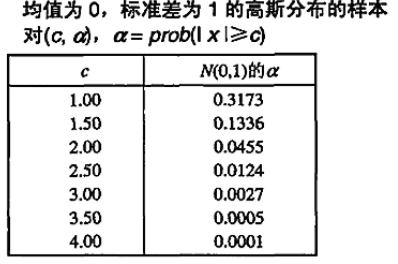
因为值到N(0,1)分布中心的距离 c 直接与该值的概率相关，因此可以使用它作为检测对象（值）是否是离群点的基础。

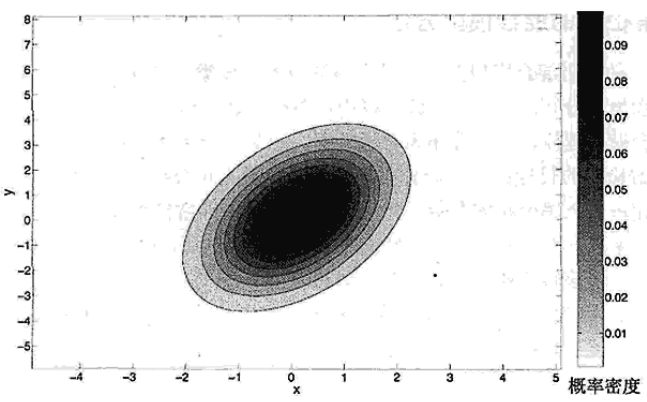
2.2  多元正态分布的离群点

由于不同变量（属性）之间的相关性，多元正态分布并不关于它的中心对称，如下图，该分布均值为（0,0），协方差矩阵为
                                                                       

 

                                   

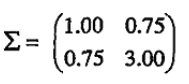
 什么是协方差矩阵： 协方差矩阵

如果我们打算用一个简单的阀值来决定一个对象是否是离群点，可以用 Mahalanobis 距离，它是是一种考虑数据分布形状的距离度量。

2.3  异常检测的混合模型方法

数据用两个分布的混合模型建模，一个分布为普通数据；另一个为离群点。

　　初始时将所有对象放入普通对象集，而异常对象集为空。然后用一个迭代过程将对象从普通集转移到异常集，只要该转移能提高数据的总似然（数据和模型之间的相似度）。

假定数据集D包含来自两个概率分布的对象：M是大多数（正常）对象的分布，A是异常对象的分布，则数据的总概率分布可以记作：D(x) = (1 - λ) + λA(x)

其中，x是一个对象，λ是一个0 - 1之间的数，给出离群点的期望比例。M由数据估计，A通常取均匀分布。初始时刻 t = 0，M₀ = D，A₀为空。在任意时刻 t，整个数据集的似然和对数似然分别为以下两式：

                                     

 

 

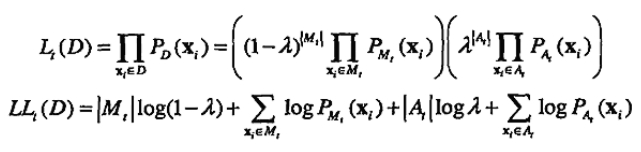
P_D、P_Mt 和 P_At 分别是 D、M_t 和 A_t 的概率分布函数。

　　因为正常对象的数量比异常对象大得多，因此当一个对象移动到异常集后，正常的分布变化不大。这时，每个正常对象对正常对象的总似然的贡献保持相对不变。

　　另外，如果假定异常服从均匀分布，则移动到异常集的每个对象对异常的似然贡献一个固定的量。这样，当一个对象移动到异常集时，数据总似然的改变粗略等于该对象在均匀分布下的概率（用λ加权）减去该对象在正常数据点的分布下的概率（用1-λ加权）。从而，异常集由这样一些对象组成，这些对象在均匀分布下的概率明显比在正常对象分布下的概率高。