Slam笔记I
科西嘉人 人气:0
# 视觉Slam笔记I
## 第二讲-三位空间刚体运动
### 点与坐标系:
#### 基础概念:
- 坐标系:左手系和右手系。右手系更常用。定义坐标系时,会定义世界坐标系,相机坐标系,以及其他关心对象的坐标系。空间中任意一点可由空间的基的线性表出。
- 加减法:用坐标描述更方便。
- 内积:点乘得数,即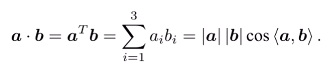
- 外积:叉乘得向量,即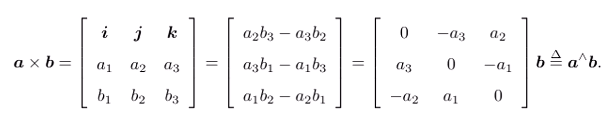右手系下,得到按照右手定则获取的向量。
- 坐标系间的变换: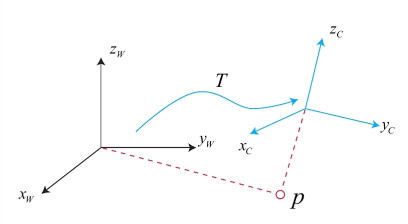
通过平移(向量的加减)和旋转(有多种描述方式,见下)
- 2D情况:二维坐标点表示位置+一个旋转角表示朝向。
- 3D情况:三维坐标点表示位置+一个旋转角(角度间的变换使用旋转,旋转方式有多种,见下)。
#### 旋转矩阵:(描述旋转的第一种方式)
坐标系` (e_1,e_2,e_3)`经过旋转变成` (e'_1,e'_2,e'_3)`,在三维空间中,向量` a`保持不动,那么如何表出它在` (e'_1,e'_2,e'_3)`下的坐标:
1. 线性表出法向量` a`坐标:两坐标系实质是分别用两组不同的基去表示同一个点,则两者的线性组合是相等的: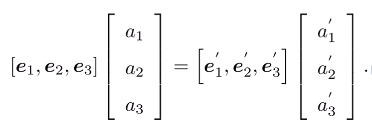
2. 左右两边同时左乘` (e_1,e_2,e_3)`的转置,得到: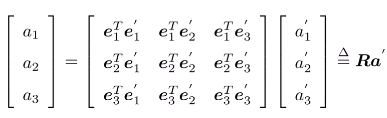
- R即为**旋转矩阵**。
- 性质:
- R是一个正交矩阵(矩阵的逆即矩阵的转置,或转置×本身即为一个单位矩阵)。
- R的行列式值为1。
- 满足上述性质的矩阵都可以称为**旋转矩阵**,使用集合表示: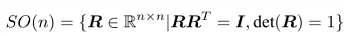
,又称特殊正交群SO(3)。
- 固定表示方式(下标顺序):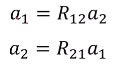且满足矩阵关系:。
**因此,空间中不同坐标系下点坐标的变换可以使用: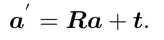即旋转+平移的形式完全描述**
- 理论依据:欧拉定理,刚体在三维空间中的一般运动,可分解为刚体上方某一点的平移,以及绕经过此点的旋转轴的转动。
但是,这种表示方式在多次进行变换时会有不便(),因此使用增广的方式进行表示:
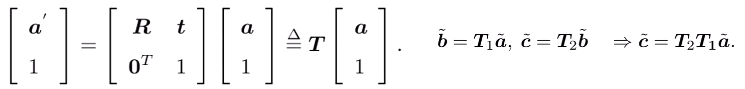
- 其中,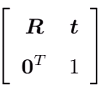称为变换矩阵,的形式称为齐次坐标。
- 齐次坐标性质:齐次坐标乘上任意非0常数时仍表达同一坐标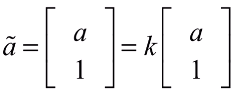
- 变换矩阵的集合:称为特殊欧式群SE(3):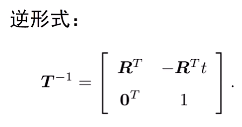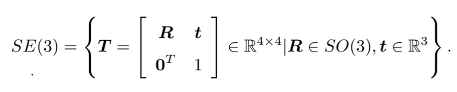
#### 旋转向量和欧拉角:
旋转矩阵在实际中更常用,但这些概念也是需要清楚的。
旋转矩阵R是一个3×3的矩阵,有九个元素,但仅有三个自由度,也就是存在描述方式上的冗余,那么能否以更少的元素表达旋转?
刚体旋转存在一个转轴(向量),还有转过的角度,于是想用**角度乘以向量**(单位化过后)的形式去描述旋转。
###### 旋转向量
- 一个向量,方向为旋转轴方向,长度为转过的角度。(单位向量乘角度大小)
- 又称角轴/轴角。
- **罗德里格斯公式**可以将旋转向量(**n**,theta)转换成旋转矩阵R: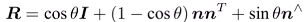
- 旋转矩阵R也可以转换成旋转向量(**n**,theta):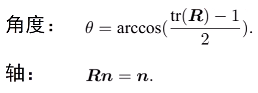**n**是特征向量。
###### 欧拉角
- 将旋转分解成三个方向上的转动,常用顺序为yaw-pitch-roll(也就是绕Z-Y-X方式转,注意 ,不同地方在绕Z转之后,所绕的Y轴可能是原来的Y轴,也可能是转动后的Y轴)
- 
- 万向锁(Gimbal Lock):欧拉角存在奇异性(特定值下,旋转的自由度减1)
- 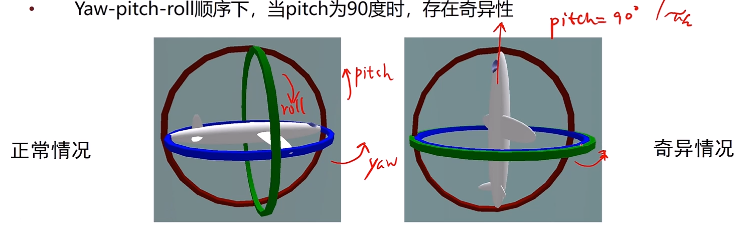在pitch方向旋转完毕后,roll方向旋转和yaw方向旋转是重合的。由此,欧拉角不适合插值或迭代,故不常用。
#### 四元数:
吸取了旋转矩阵和旋转向量、欧拉角的优点,是一种优秀的描述方式。
- 2D情况下,可以用单位复数表达旋转:
$$
z=x+iy=\rho e^{i\theta}
$$
- 用z乘以i,相当于旋转了90度(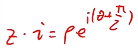),乘-i转动-90度。
在三维情况下,四元数可作为扩充定义的复数
- 特点1:有三个虚部+一个实部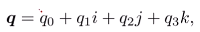
- 特点2:虚部之间存在关系:
- 单位四元数可以表达三维空间的旋转:
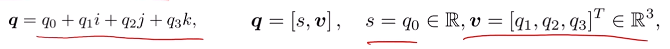
- 四元数也能定义很多运算:
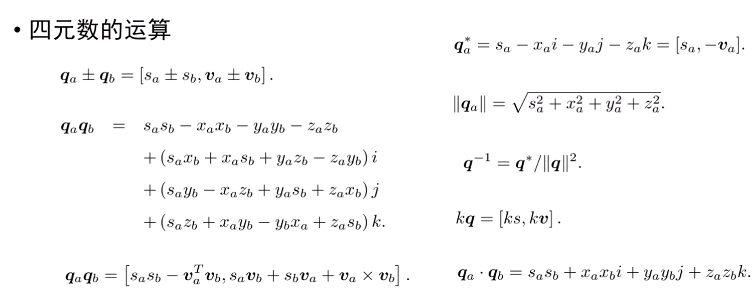
- 四元数转换成旋转向量: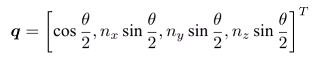
- 旋转向量转换成四元数: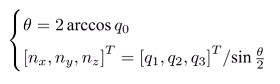
- 用四元数表示旋转:

加载全部内容