【面试QA-基本模型】RNN 与 CNN
西多士NLP 人气:2目录
为什么传统 CNN 适用于 CV 任务,RNN 适用于 NLP 任务
从模型特点上来说:
对于 CNN 每一个卷积核都可以看作是一个滤波器,卷积运算的本质是互相关运算,每个卷积核仅对于具有特定特征具有较大的激活值,而且 CNN 有参数共享和局部连接的特点,能够提取图像上不同位置的同一个特征,即 CNN 具有平移不变性
RNN 的特点在于其是一个时序模型,在对每个神经元不仅可以接收当前时刻的输入信息,还将接收上一个时刻的该神经元的输出信息,具有短期记忆能力。这在用于 NLP 任务时相当于隐含着建立了一个语言模型,这对词序具有很强的区分能力。而 CNN 和 DNN 均类似词袋模型,丢失的词序特征。
从数据特征上来说
- 图像矩阵中的每个元素为图像中的像素值,每个像素与其周围元素都是高度相关的
- 文本矩阵中的数据为词的 embedding 向量,每个元素在词向量内与词向量间的相邻元素的关联性是不同的,因此 CNN 用于 NLP 任务常使用的是一维卷积
CNN 与 FCN 相比有什么优点?
- CNN 相比于 FCN 具有更少的参数,主要有下面两个原因:
- 参数共享:一个卷积核能对样本图像上的所有区域采用相同的参数进行特征检测。
- 稀疏连接:在每一层中,由于滤波器的尺寸限制,输入和输出之间的连接是稀疏的,每个输出值只取决于输入在局部的一小部分值。
- 池化层降维:池化过程则在卷积后很好地聚合了特征,通过降维来减少运算量。
- 由于 CNN 参数数量较小,所需的训练样本就相对较少,因此在一定程度上不容易发生过拟合现象。
- 平移不变性:CNN 比较擅长捕捉区域位置偏移。即进行物体检测时,不太受物体在图片中位置的影响,增加检测的准确性和系统的健壮性。
CNN的相关计算
- 输出维度计算
- 输出维度 = (输入维度 - 卷积核大小 + 2*Padding长度)/步长 + 1
- 感受野的计算
- 第k层的感受野 = 第k-1层的感受野 + ((第k-1层的卷积核大小)*\prod_{i=1}^{k-1}步长)
- 卷积核的参数量
- 参数量=(filter size * 输入通道数 )* 当前层 filter 数量
- 卷积核的计算量
- 计算量 = 输出的维度^2 * 输出的通道数 * 卷积核个数 * 卷积核大小^2
RNN 原理
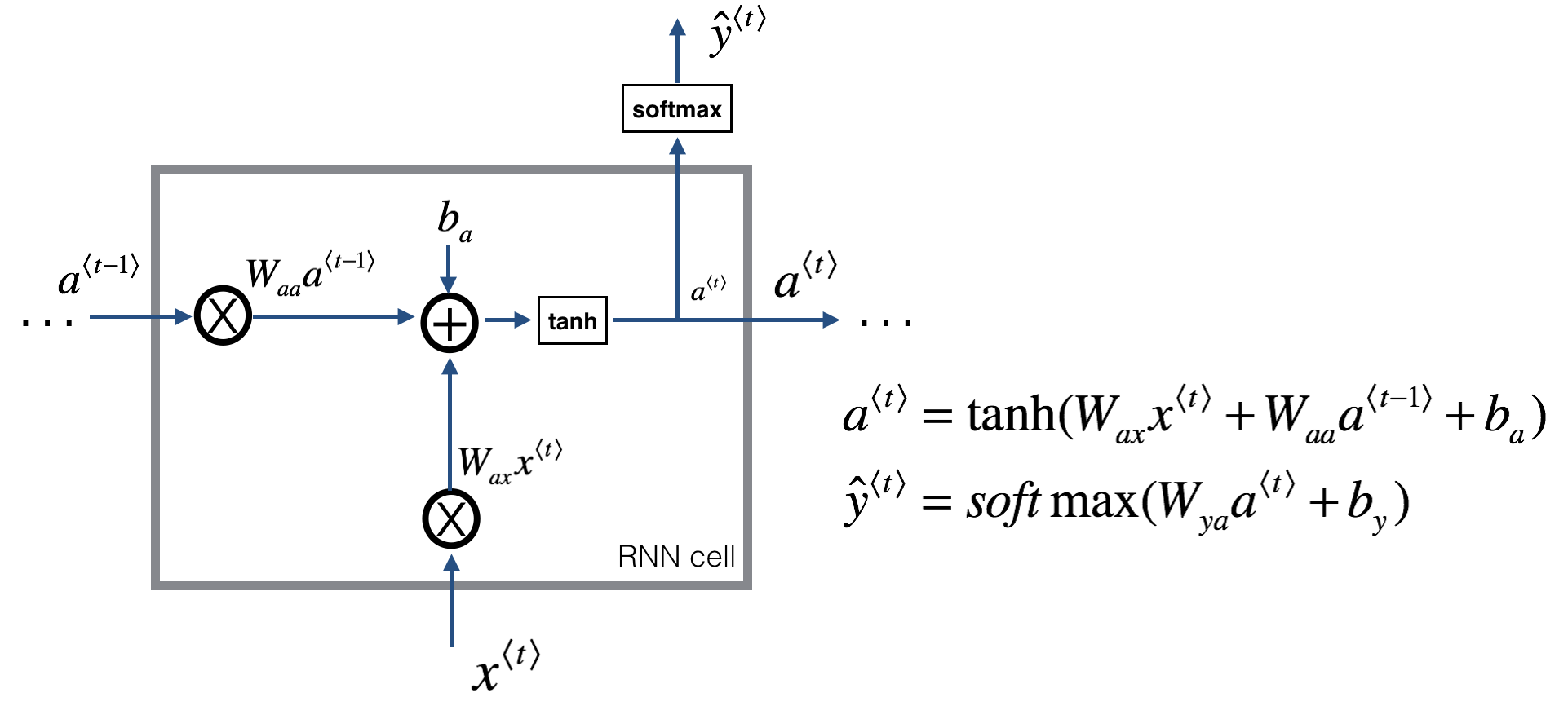
\(\hat y\) 部分的激活函数可以根据下游任务设置
LSTM 原理
- 三个门:[output_dim + input_dim, 1]
- 更新门位置的全连接层:[output_dim + input_dim, output_dim]

GRU 原理
- 两个门:[output_dim + input_dim, 1]
- 全连接层:[output_dim + input_dim, output_dim]

RNN BPTT

假设\(t\)时刻的损失函数为\(L_t\),以 \(W_{aa}\),\(W_{ax}\),\(W_{ya}\) 为例
\[ \begin{aligned} &\frac{\delta L_t}{\delta W_{ya}} = \frac{\delta L_3}{\delta \hat{y}_t}\frac{\delta \hat{y}_t}{\delta W_{ya}} \\ &\frac{\delta L_t}{\delta W_{aa}} = \frac{\delta L_t}{\delta \hat{y}_t}\frac{\delta \hat{y}_t}{\delta a_{t}}(\frac{\delta a_{t}}{\delta W_{aa}} + \frac{\delta a_{t}}{\delta a_{t-1}}\frac{\delta a_{t-1}}{\delta W_{aa}} + ...)\\ &\frac{\delta L_t}{\delta W_{ax}} = \frac{\delta L_3}{\delta \hat{y}_t}\frac{\delta \hat{y}_t}{\delta a_{t}}(\frac{\delta a_{t}}{\delta W_{ax}} + \frac{\delta a_{t}}{\delta a_{t-1}}\frac{\delta a_{t-1}}{\delta W_{ax}} + ...) \end{aligned}\]对于任意时刻t对 \(W_x\),\(W_s\) 求偏导的公式为:
\[\begin{aligned} &\frac{\delta L_t}{\delta W_{aa}} = \sum_{k=0}^{t}\frac{\delta L_t}{\delta y_t}\frac{\delta y_t}{\delta a_t}( \prod_{j=k+1}^t\frac{\delta a_j}{\delta a_{j-1}} ) \frac{\delta a_k}{\delta W_{aa}}\\ &\frac{\delta L_t}{\delta W_{aa}} = \sum_{k=0}^{t}\frac{\delta L_t}{\delta y_t}\frac{\delta y_t}{\delta a_t}( \prod_{j=k+1}^t\frac{\delta a_j}{\delta a_{j-1}} ) \frac{\delta a_k}{\delta W_{aa}} \end{aligned}\]其中\(\frac{\delta a_j}{\delta a_{j-1}}\)和\(\frac{\delta a_k}{\delta W_{aa}}\)还存在\(tanh'\)的导数项,而\(tanh'\)的值域为\((0, 1)\)。随着时间步的增长,累乘项会趋于 0,出现梯度消失的问题
LSTM 如何解决 RNN 的梯度消失问题
- RNN 的激活函数为 \(tanh\),而 \(tanh\) 的导数取值范围为 \([0, 1]\),在时间上的反向传播会存在时间上的梯度累乘项,时间步长了会导致梯度累乘而消失
- LSTM 通过引入全局信息流,在时间维度上引入残差结构,残差结构的引入就使得链式求导过程中引入了一个求和项,从反向传播的求导来看,最多只有两个激活函数的导数累乘,因此远距离的梯度通常都可以正常传播,减弱了梯度消失问题
怎样增加 LSTM 的长距离特征提取能力
- Dilated RNN:Dilated CNN 为空洞卷积,Dilated RNN 则是在时间维度上空洞,浅层部分的为传统 RNN,每个时间步都循环,深层的循环周期更长,增大时间维度上的“感受野”
加载全部内容