DS博客作业02--栈和队列

# 0.PTA得分截图 # 1.本周学习总结 ## 1.1总结栈和队列内容 * 栈的存储结构及操作 * 栈的顺序存储结构 ``` typedef struct { ElemType data[MaxSize]； int top； //栈顶指针 } Stack； typedef Stack *SqStack; ``` * 顺序栈的四要素 栈空条件：top=-1 栈满条件: top=MaxSize-1; 进栈e操作:top++;st->data[top]=e; 退栈操作:e=st->data[top];top--; * 顺序栈操作 * 初始化栈 ``` void InitStack(&s) { s=new Stack; s->top=-1; } ``` * 销毁栈 ```` void DestroyStack(SqStack &s) { 　　delete s; } ```` * 判断栈是否为空 ``` bool StackEmpty(SqStack s) { 　　return(s->top==-1); } ``` * 进栈 ```` bool Push(SqStack &s，ElemType e) { if (s->top==MaxSize-1) //栈满的情况，即栈上溢出 return false; s->top++; //栈顶指针增1 s->data[s->top]=e; //元素e放在栈顶指针处 return true; } ```` * 出栈 ``` bool Pop(SqStack &s，ElemType &e) { if (s->top==-1) //栈为空的情况，即栈下溢出 return false; e=s->data[s->top]; //取栈顶指针元素的元素 s->top--; //栈顶指针减1 return true; } ``` * 取栈顶元素 ```` bool Pop(SqStack &s，ElemType &e) { if (s->top==-1) //栈为空的情况，即栈下溢出 return false; e=s->data[s->top]; //取栈顶指针元素的元素 s->top--; //栈顶指针减1 return true; } ```` * 栈的链式存储结构 ``` typedef struct linknode { ElemType data; //数据域 struct linknode *next; //指针域 } LiNode,*LiStack; ``` * 链栈的四要素 栈空条件：s->next=NULL 栈满条件：不考虑 进栈e操作：将包含e的结点插入到头结点之后 退栈操作：取出头结点之后结点的元素并删除之 * 链栈的操作 * 初始化栈 ```` void (LinkStNode *&s) { s= new LiNode; s->next=NULL; } ```` * 销毁栈 ``` void DestroyStack(LiStack &s) {　 LiStack p=s，q=s->next; while (q!=NULL) { free(p); p=q; q=p->next; } delete p; //此时p指向尾结点，释放其空间 } ``` * 判断栈空 ```` bool StackEmpty(LiStack s) { return(s->next==NULL); } ```` * 进栈 ``` void Push(LiStack &s，ElemType e) { LiStack p; p=new LiNode; p->data=e; //新建元素e对应的结点*p p->next=s->next; //插入*p结点作为开始结点 s->next=p; } ``` * 出栈 ```` bool Pop(LiStack &s，ElemType &e) { LiStack p; if (s->next==NULL) //栈空的情况 return false; p=s->next; //p指向开始结点 e=p->data; s->next=p->next; //删除*p结点 delete p; //释放*p结点 return true; } ```` * 取栈顶元素 ``` bool GetTop(LiStack s，ElemType &e) { if (s->next==NULL) //栈空的情况 return false; e=s->next->data; return true; } ``` * 栈的应用 * 表达式求值  ``` while （读取字符ch且ch!='\0') { 若ch为数字：将后续的所有数字依次存放到postexp中， 若ch为左括号'('：将此括号进栈; ch为右括号')'：出栈时遇到的第一个左括号'('以前的运算符依次出栈并存放到postexp中，然后将左括号'('出栈; ch为其他运算符： if （栈空或者栈顶运算符为'('） 直接将ch进栈; else if (ch的优先级高于栈顶运算符的优先级) 直接将ch进栈; else 依次出栈存入到postexp中，直到栈顶运算符优先级小于ch的优先级，然后将ch进栈; } 若exp扫描完毕，则将栈中所有运算符依次出栈并存放到postexp中。 ``` * 顺序队 * 存储结构 ``` typedef struct { ElemType data[MaxSize]； int front,rear； //队首和队尾指针 } SqQueue,*SqQueue; ``` * 四要素 ``` 队空条件：front = rear 队满条件：rear = MaxSize－1 元素e进队：rear++; data[rear]=e; 元素e出队：front++; e=data[front]; ``` * 初始化队列 ``` void InitQueue(SqQueue &q) {　 q=new SqQueue; 　 q->front=q->rear=-1; } ```  * 销毁队列 ``` void DestroyQueue(SqQueue &q) { delete q } ``` * 判断队空 ``` bool QueueEmpty(SqQueue *q) { return(q->front==q->rear); } ``` * 进队 ``` bool enQueue(SqQueue &q,ElemType e) { if (q->rear==MaxSize-1) //队满上溢出 return false; q->rear++; q->data[q->rear]=e; return true; } ```  * 出队 ``` bool deQueue(SqQueue &q,ElemType &e) { if (q->front==q->rear)　　//队空下溢出 return false; q->front++; e=q->data[q->front]; return true; } ```  * 环形队列 * 四要素 ``` 队空条件：front = rear 队满条件：(rear+1)%MaxSize = front 进队e操作：rear=(rear+1)%MaxSize; 将e放在rear处 出队操作：front=(front+1)%MaxSize; 取出front处元素e; ``` * 存储结构 ``` typedef struct { ElemType data[MaxSize]; int front; //队头指针 int count; //队列中元素个数 } QuType，QuType; ``` * 初始化队列 ``` void InitQueue(QuType &qu) //初始化队运算算法 { qu=new Qutype; qu->front=0; qu->count=0; } ``` * 进队 ``` bool EnQueue(QuType &qu,ElemType x) //进队运算算法 { int rear; //临时队尾指针 if (qu->count==MaxSize) //队满上溢出 return false; else { rear=(qu->front+qu->count)%MaxSize; //求队尾位置 rear=(rear+1)%MaxSize; //队尾循环增1 qu->data[rear]=x; qu->count++; //元素个数增1 return true; } } ``` * 出队 ``` bool DeQueue(QuType &qu,ElemType &x) //出队运算算法 { if (qu->count==0) //队空下溢出 return false; else { qu->front=(qu->front+1)%MaxSize; //队头循环增1 x=qu->data[qu->front]; qu->count--; //元素个数减1 return true; } } ``` * 判空 ``` bool QueueEmpty(QuType &qu) //判队空运算算法 { return(qu->count==0); } ``` * 链队    * 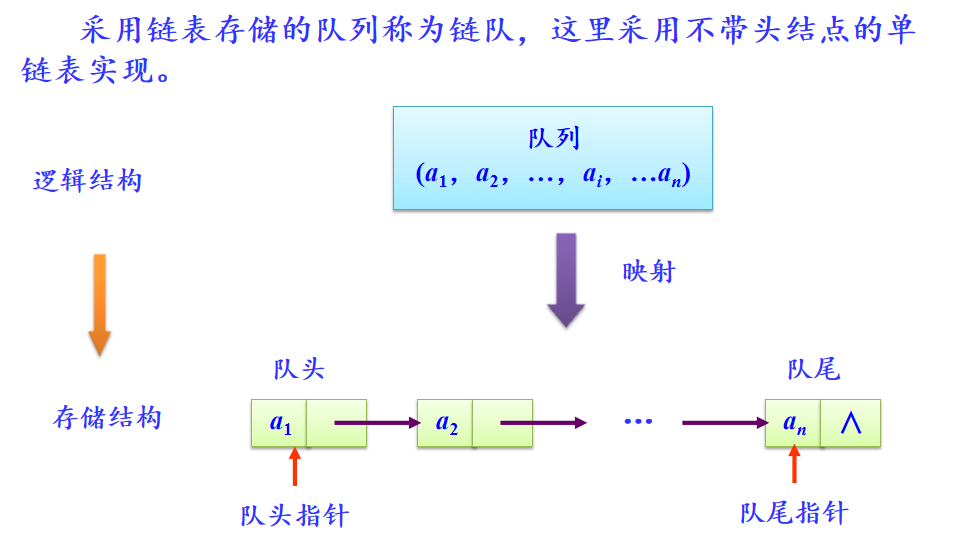存储结构 ``` typedef struct { elemtype data; DataNode *front; //指向单链表队头结点 DataNode *rear; //指向单链表队尾结点 } LinkQuNode, *LinkQuNode; ``` * 四要素 ``` 队空条件：front=rear=NULL 队满条件：不考虑 进队e操作：将包含e的结点插入到单链表表尾 出队操作：删除单链表首数据结点 ``` * 初始化 ``` void InitQueue(LinkQuNode &q) { q= new LinkQuNode; q->front=q->rear=NULL; } ``` * 销毁队列 ``` void DestroyQueue(LinkQuNode &q) { LinkQuNode p=q->front，r; //p指向队头数据结点 if (p!=NULL) //释放数据结点占用空间 { r=p->next; while (r!=NULL) { free(p); p=r;r=p->next; } } delete p; delete q; //释放链队结点占用空间 } ``` * 判空 ``` bool QueueEmpty(LinkQuNode q) { 　　return(q->rear==NULL); } ``` * 进队 ``` void enQueue(LinkQuNode &q，ElemType e) { LinkQuNode p; p=new LinkQuNode; p->data=e; p->next=NULL; if (q->rear==NULL) //若链队为空，新结点是队首结点又是队尾结点 q->front=q->rear=p; else { q->rear->next=p; //将*p结点链到队尾，并将rear指向它 q->rear=p; } } ``` * 出队 ``` bool deQueue(LinkQuNode &q，ElemType &e) { LinkQuNode t; if (q->rear==NULL) return false; //队列为空 t=q->front; //t指向第一个数据结点 if (q->front==q->rear) //队列中只有一个结点时 q->front=q->rear=NULL; else //队列中有多个结点时 q->front=q->front->next; e=t->data; delete t; return true; } ``` * 队列的应用 * 求解迷宫 ``` while (队不空循环) { 出队方块e if (找到了出口,输出路径) } for (循环扫描每个方位) { switch(di) { 四个方位的前进 } if (死路) { e.i=i1; e.j=j1; e.pre=qu->front; enQueue(qu,e); //(i1，j1)方块进队 mg[i1][j1]=-1; //将其赋值-1 } } DestroyQueue(qu); //销毁队列 return false; ``` ## 1.2 对栈和队列的认识和体会 * 先产生的数据后处理―栈（先进后出表） * 先产生的数据先处理―队列（先进先出表） * 顺序栈和队列，要考虑满和空的条件。不同的定义由不同的条件。 * 生活中不乏先来后到或特殊顺序的秩序流程，相关问题适合用栈或者队列加以解决。