详解隐马尔科夫模型

隐马尔科夫模型

摘要

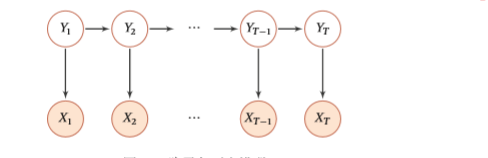
本文重点讲解隐马尔科夫(HMM)模型的模型原理，以及与模型相关的三个最重要问题：求解、解码和模型学习。 #### 隐马尔科夫模型的简单介绍 为了方便，下文统一用HMM代替隐马尔科夫模型。HMM实际上是一种图概率模型。之所以叫做隐马尔科夫模型，是因为模型与普通的马尔科夫模型不同的是，HMM含有隐变量空间，并且遵循马尔科夫假设。这样说太抽象，我们看下图：  其中$Y_i\in Q={q_1,q_2,...,q_N}$，$X_i \in V={v_1,v_2,...,v_M}$。并且记观测序列$X = X_1,X_2,...,X_T$ 隐状态序列$Y = Y_1,Y_2,...,Y_T$。我们首先介绍HMM三个重要参数，然后下面再解释这些参数的具体物理含义。 $$ 状态转移矩阵： A = [a_{ij}]N\times N \\ a_{ij} =P(Y_t=q_j|Y_{t-1}=q_i),i=1,2,...,N\\ 观测概率矩阵: B = [b_{jk}]N\times M \\ b_{jk} = P(X_t=v_k|Y_t=q_j), j = 1,2,...,N;k=1,2,...,M\\ 初始分布： \pi=[\pi_1,\pi_2,...,\pi_N]\\ \pi_i = P(Y_0=q_i),i = 1,2,...,N $$ 也就是说，状态转移概率决定了状态间的单步转移情况，而观测发射矩阵决定了从隐状态到观测状态的转移情况。而初始分布决定了模型的状态初始分布。为了叙述方便，我们记上面的参数为$\lambda=(A,B,\pi)$ HMM有如下两个假设，齐次性质假设和观测独立性假设，分别叙述如下： - 齐次马尔科夫假设： $$ P(Y_t|X_1,...,X_{t-1},Y_1,...,Y_{t-1})=P(Y_t|Y_{t-1}) $$ 也就是任何时刻的隐藏状态只与上一时刻的隐藏状态有关，与其他的隐藏状态和观测状态无关。 - 观测独立性假设： $$ P(X_t|X_1,...,X_T,Y_1,...,Y_T)=P(X_t|Y_t) $$ 即任意时刻的观测只由其同时刻的隐状态所决定，与其他隐藏状态和观测状态无关。 为了更形象的理解这个模型，下面举一个我觉得比较贴切的例子。 假设有两个人分别记为P1和P2，他们中间隔了一堵墙。其中P1被关在了墙里面，P2在外面。这两个人仅仅能通过一个窗子交流。两个人分别有以下的特点：P1记性特别差，只能记住上一次说过的单词。并且每次说话时也只受上一次说话内容所影响。而P2可以看成一个特殊的转录机，他每次说的单词都只受P1当前说的单词所影响。并且P2有一个很长的纸带，会把每次说的单词记录下来。并且假设P1和P2的词汇表都是有限的。 - 如果给定P2的文本片段，我们能否给出该文本片段的概率(已知模型参数$\lambda$) - 给定P2的文本片段，假设我们已经知道了P1的词汇表，我们能否给出P1最可能说了哪段话（已知模型参数$\lambda$) - 给定大量的(P2,P1)文本对片段，能否推测出模型参数$\lambda$,或者仅仅给出大量的P2文本片段，能否学出模型参数$\lambda$ 实际上面的三个问题就对应着预测，解码和模型学习的三个问题。并且如果P1的词汇表是分词标记标签，P2的词汇表是汉语，那么所对应的就是分词问题。把P1的词汇表是命名实体标签，P2的词汇表是汉语，那么所对应的问题实际上就是命名实体识别（NER）问题。 如果我们不关心模型的具体使用，只是关心HMM是一个什么样的模型，那么到这里完全可以将模型说明白。但是我们要更细致的了解HMM的话（从代码层面上）那么还是逐一解决上述三个重要的问题。 #### 预测问题 所谓的预测问题，实际上是求下面的序列概率： $$ p = P(X_1,X_2,...,X_T;\lambda) $$ 根据全概率公式我们有： $$ \begin{align*} p&=P(X_1,X_2,...,X_T;\lambda)\\ &=\sum_{Y}P(X_1,X_2,...,X_t,Y_1,Y_2,...,Y_t;\lambda) \end{align*} $$ 其中$Y$是隐状态空间的内所有组合，显然当隐状态空间特别大时，如果通过简单的枚举加和方式，面临着指数爆炸这一难题（简单的分析可知，上述的求和复杂度是$O(N^T)$）。 通过上述分析可知，高效的求解序列概率的关键在于求解联合概率。根据链式法则及HMM的假设我们可以得到如下公式： $$ \begin{align*} P(X_{<=T},Y_{<=T};\lambda)& = P(X_1,X_2,...,X_T,Y_1,Y_2,...,Y_T;\lambda) \\ &=P(X_T,Y_T|X_1,...,X_{T-1},Y_1,...,Y_{T-1}) \cdot P(X_1,...,X_{T-1},Y_1,...,Y_{T-1})\\ &=P(X_T|Y_T) \cdot P(Y_T|Y_{T-1})\cdot P(X_{