数的机器码表示——彻底弄清什么是原码、反码、补码、移码
清雨无尘 人气:2
## 数的机器码表示
@[toc]
为了妥善的处理数据运算过程中符号位的问题,于是就产生了**把符号位和数值位一起编码**起来**表示相应的数**的各种表示方法。例如我们熟悉的原码、反码、补码、移码等。通常将未经**编码的数称为真值**,编码后的数称为**机器数或者机器码**。
- **真值的形式**:**正、负号加某进制数绝对值的形式**,即**数的实际值**。如`+3`,`-5`等
- **机器数的形式**:真值按某种编码方式进行编码后的数值,即**真值在机器中的表示**,称为机器数,一般可以分为 **无符号数和有符号数**两种如:**X=01011** ,**Y=11011**
### 原码
#### 定点整数
若定点整数的原码形式位$x_n x_{n-1}\cdot\cdot\cdot x_1x_0$,其中$x_n$为符号位,则原码表示的定义为:
$$
x_{[原]}=\left\{\begin{matrix}
x & 0 \leqslant x<2^n \\
2^n-x=2^n+|x| & -2^n0000
- -0
- 1000-->1111
#### 定点小数
假设定点小数的反码形式为$x_s.x_1x_2...x_n$(**实际上小数点是不存储的**),其中$x_s$代表符号位。则反码的定义为:
$$
x_{[反]}=\left\{\begin{matrix}x & 0 \leqslant x<1 \\ 2-2^{-n}+x=2-2^{-n}-|x| & -1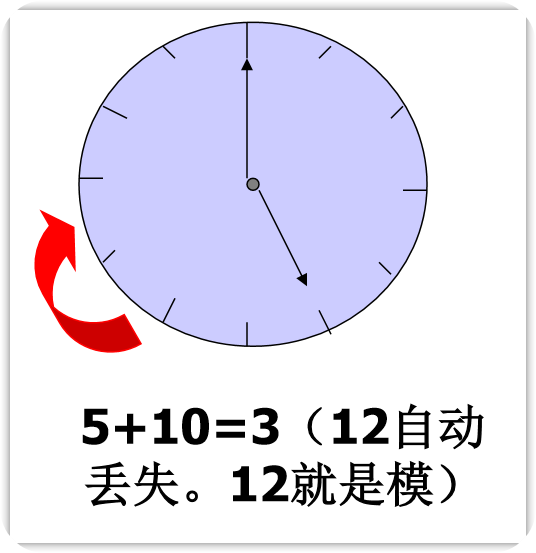 我们既可以顺时针调也可以逆时针调。也就是说我们$5-2$和$5+10$的效果是一样的。
而把这种思想引入到计算机中,不就可以把减法转为加法了吗?
$$
5-2=5+10(MOD 12) \\5+(-2)=5+10(MOD 12)\\ -2=10(MOD 12)
$$
在上面的式子中,在**模为12的情况下,-2的补码就是10**。一个负 数用其补码代替,同样可以得到正确的运算结果。
那什么是**模**呢?
> 计算机中运算器、寄存器、计数器都有一定的位数,不可能容纳无限大的任意数。当运算结果超出实际的最大表示范围, 就会发生溢出,此时所产生的**溢出量**就是**模(module)**
可以把模定义为一个**计量器的容量**。
如一个**八位计数器**,`0000 0000~1111 1111`,它表示的范围就是`[0,255]`。当计数器表示为`1111 1111` 时,如果**计数器再加一**,那么此计数器就会溢出。计数器上的数值会变成**0000 0000**.而此计数器的溢出量就是**256**.
假设此计数器表示一个定点小数,它表示的范围就是[0,2-$2^{-8}$]。当表示最大的时候,计数器值为**1.111 1111**当**计数器加一**的时候,那么计数器就会清零,变为**0.0000000**。那么此此定点小数的溢出量就是**2**.
从上面我们可以推导出,一个`n+1`位定点整数$x_n x_{(n-1)} ... x_2 x_1 x_0$,它的溢出量为$2^{n+1}$,所以模为$2^{n+1}$。
任意一个定点小数$x_s.x_1x_2...x_n$,它的溢出量是2,所以模为2。
而**在计算机中**,机器能表示的**数据位数是固定**的, 其**运算都是有模运算**。若运算结果**超出**了计算机所能表示的数值范围, 则只**保留它的小于模的低n+1位**的数值,**超过n+1 位**的高位部分就**自动舍弃**了。
下面我们来引入**补码的定义**:
#### 定点整数
定点整数的补码形式为$x_n x_{n-1}\cdot\cdot\cdot x_1x_0$,其中$x_n$为符号位,补码表示的定义为:
$$
x_{[补]}=\left\{\begin{matrix}x & 0 \leqslant x<2^n \\ 2^{n+1}+x=2^{n+1}-|x| & -2^n \leqslant x\leqslant0\end{matrix}\right.
$$
在上式中,**x代表的是真值**。
例如,$x=+7$,化为二进制表示为$x=+0111$;$x_{[补]}=0111$。
$x=-7$,化为二进制表示为$x=-0111$;$x_{[补]}=2^4+(-0111)=10000-0111=1001$。
我们可以总结出来:
- 对于正数$x=+x_{n-1}...x_1x_0$,它的补码是它自己本身,常常在最高位前面补0,代表它是一个正数。
- $x_{[补]}=0_nx_{n-1}...x_1x_0$
- 对于0,根据补码的定义:
- $+0=+0_{n-1}...0_10_0$
- 此时正0的补码为$+0_{[补]}=0_n0_{n-1}...0_10_0$
- $-0=-0_{n-1}...0_10_0$
- 此时负0的补码为$-0_{[补]}=(10_n0_{n-1}...0_10_0-0_{n-1}...0_20_10_1)mod(10_n0_{n-1}...0_10_0)=0_n0_{n-1}...0_10_0$
由此可见,**零的补码是唯一的**,没有+0和-0之分。
- 对于负数$x=-x_{n-1}...x_1x_0$
常常可以通过把**数值位按位取反**,然后**末位加一来计算负数的补码**。
- 如求$-127$的补码
- $[-0111 1111]_{[补]}=10000 0000-01111111 $
- $10000000=11111111+1$
- $[-0111 1111]_{[补]}=11111111-01111111+1$,这一步刚刚说明了上面的计算方法的原理。
$-128$的补码的求法。
- -128=-1000 0000
- $[-10000000]_{[补]}=11111111-10000000+1=10000000$
其实还有一个更为渐变的补码的求法:**从右到左遇到第一个 1 的前面各位取反。**也就是从右向左,遇到1之前,还保持原样。遇到1之后,各位取反。以-126为例:$-126=-01111110$
[-01111110]的补码位**100000**10,10是不变的。而黑体部分则是取反的。
对于补码的取值范围,10000000-11111111——- $-128$~$-1$
00000000~011111111 ——0~127
推广到n位数,则**补码的范围**就是[$-2^{n-1},2^{n-1}-1$]
#### 定点小数
定点小数的补码形式为$x_s.x_1x_2...x_n$(**实际上小数点是不存储的**),其中$x_s$代表符号位。则补码的定义为:
$$
x_{[原]}=\left\{\begin{matrix}x & 0 \leqslant x<1 \\ 2+x=2-|x| & -1\leqslant x\leqslant0\end{matrix}\right.
$$
在上式中,x代表的是真值。
例如,$x=+0.875$,化为二进制表示为$x=+0.111$;$x_{[补]}=0.111$。
$x=-0.875$二进制表示为$x=-0.111$;$x_{[补]}=10.000-(0.111)=1.001$。
我们可以总结出来:
- 对于正数$x=+0.x_{n-1}...x_1x_0$,它的补码是它自己本身,常常在最高位前面补0,代表它是一个正数。(注意,**前面的0.实际上是不存储的**,也就是实际最高位是$x_{n-1}$)
- $x_{[原]}=0.x_{n-1}...x_1x_0$
- 对于0,根据补码的定义:
- $+0=+0.0_{n-1}...0_10_0$
- 此时正0的补码为$+0_{[补]}=0.0_{n-1}...0_10_0$
- $-0=-0.0_{n-1}...0_10_0$
- 此时负0的补码为$-0_{[补]}=(10.0_{n-1}...0_10_0-0.0_{n-1}...0_10_0)mod(10.0_{n-1}...0_10_0)=0.0_{n-1}...0_10_0$
也就是说**,0的补码是唯一的**。
- 对于负数
按位取反,末位加一,和定点整数一样。虽然我们看起来有一个小数点,但是实际上小数点是不存储的。
定点小数的补码的范围,0000~0111--> [0,0.875]
1000~1111--> [-1,-0.125]
扩展到n位补码
我们很容易求出它的范围$[-1,1-2^{-(n-1)}] $
#### 补码的运算
假设一个二进制整数补码有n+1位,$x_nx_{n-1}...x_2x_1x_0$,则补码与真值的对应关系可以这么表示:
$X_{真值}=-2^n\times x_n+\sum_{0}^{n-1}2^ix_n$
当该数为正整数的时候,$x_n$位变为0,$0x_{n-1}...x_2x_1x_0$,
$X_{真值}=\sum_{0}^{n-1}2^ix_n$
当该数为负整数的时候,$x_n$位变为1,$1 x_{n-1}...x_2x_1x_0$,
$X_{真值}=-2^n+\sum_{0}^{n-1}2^ix_n$
- 以-127为例,-127=-01111111
- 它的补码为10000001
- 从补码求真值的过程:-10000000+1=-01111111-1+1=-01111111
上面我们说到过,计算机中用原码进行加减运算是十分麻烦的,那么我们来看一下用补码来运算。
$126-127=0$
- 原码
- $01111110-01111111$
- 我们需要比较数值位的绝对值大小,来决定符号位,1
- 1111111-1111110=0000001
- 10000001
假设把减法看成加法
- 01111110+(-01111111)=01111110+11111111=**1**00000001
- 1会溢出,那么得到的结果就是00000001,按原码表示的化,真值为1,显然是错误的。
- 补码
- 01111110+10000001=11111111
- 转换为真值后为-1。正确的
- 原理是这样的
- 126-127=-1
- 126+(-127)=-1
- 126+129mod256=-1
- 这里-127等效于129mod256
由此,我们可以看出,补码实际上是**可以直接带符号位运算的运算**的。
求相反数的补码:**由[X]补求[-X]补**
**带符号位一起取反,然后末位加一**
如求我们**已知+127的补码求-127的补码**:
- 01111111
- 10000001
### 移码
移码通常用于表示浮点数的阶码。由于阶码是k位的整数,假设定点整数移码形式为$e_ke_{k-1}...e_2e_1e_0$最高位为符号位是。移码的传统定义是:
$[e]_移=2^k+e$
上式中,e为真值,$2^k$为固定的偏移值常数。
**与[x]补的区别:符号位相反**
| 真值 | 补码 | 移码 |
| ---- | ------ | ------- |
| -8 | 1000 | 0000 |
| -7 | 1001 | 0001 |
| -6 | 1002 | 0002 |
| …… | ...... | ...... |
| 0 | 0000 | 1000 |
| +1 | 0001 | 1001 |
| …… | ...... | ....... |
| +7 | 0111 | 1111 |
#### 移码的表示
移码表示的机器数为数的真值在数轴上向右平移了 固定的偏移值。
如八位移码:

#### 移码的特点
- 在移码中,最高位为0表示负数,最高位为1表示正数,这与**原 码、补码、反码的符号位取值正好相反**。
- 移码为全0时所对应的真值最小,为全1时所对应的真值最大! 因此,**移码的大小直观地反映了真值的大小,这将有助于两个 浮点数进行阶码大小比较**。
- 真值0在移码中的表示形式是**唯一**的,即:**[+0]移= [0]移= 100…00**
- 移码**把真值映射到一个正数域**,所以可将移码视为无符号数, 直接按无符号数规则比较大小。
- 同一数值的移码和补码除最高位相反外,其他各位相同。
### 原码、反码、补码、移码
取值范围的一个比较

我们既可以顺时针调也可以逆时针调。也就是说我们$5-2$和$5+10$的效果是一样的。
而把这种思想引入到计算机中,不就可以把减法转为加法了吗?
$$
5-2=5+10(MOD 12) \\5+(-2)=5+10(MOD 12)\\ -2=10(MOD 12)
$$
在上面的式子中,在**模为12的情况下,-2的补码就是10**。一个负 数用其补码代替,同样可以得到正确的运算结果。
那什么是**模**呢?
> 计算机中运算器、寄存器、计数器都有一定的位数,不可能容纳无限大的任意数。当运算结果超出实际的最大表示范围, 就会发生溢出,此时所产生的**溢出量**就是**模(module)**
可以把模定义为一个**计量器的容量**。
如一个**八位计数器**,`0000 0000~1111 1111`,它表示的范围就是`[0,255]`。当计数器表示为`1111 1111` 时,如果**计数器再加一**,那么此计数器就会溢出。计数器上的数值会变成**0000 0000**.而此计数器的溢出量就是**256**.
假设此计数器表示一个定点小数,它表示的范围就是[0,2-$2^{-8}$]。当表示最大的时候,计数器值为**1.111 1111**当**计数器加一**的时候,那么计数器就会清零,变为**0.0000000**。那么此此定点小数的溢出量就是**2**.
从上面我们可以推导出,一个`n+1`位定点整数$x_n x_{(n-1)} ... x_2 x_1 x_0$,它的溢出量为$2^{n+1}$,所以模为$2^{n+1}$。
任意一个定点小数$x_s.x_1x_2...x_n$,它的溢出量是2,所以模为2。
而**在计算机中**,机器能表示的**数据位数是固定**的, 其**运算都是有模运算**。若运算结果**超出**了计算机所能表示的数值范围, 则只**保留它的小于模的低n+1位**的数值,**超过n+1 位**的高位部分就**自动舍弃**了。
下面我们来引入**补码的定义**:
#### 定点整数
定点整数的补码形式为$x_n x_{n-1}\cdot\cdot\cdot x_1x_0$,其中$x_n$为符号位,补码表示的定义为:
$$
x_{[补]}=\left\{\begin{matrix}x & 0 \leqslant x<2^n \\ 2^{n+1}+x=2^{n+1}-|x| & -2^n \leqslant x\leqslant0\end{matrix}\right.
$$
在上式中,**x代表的是真值**。
例如,$x=+7$,化为二进制表示为$x=+0111$;$x_{[补]}=0111$。
$x=-7$,化为二进制表示为$x=-0111$;$x_{[补]}=2^4+(-0111)=10000-0111=1001$。
我们可以总结出来:
- 对于正数$x=+x_{n-1}...x_1x_0$,它的补码是它自己本身,常常在最高位前面补0,代表它是一个正数。
- $x_{[补]}=0_nx_{n-1}...x_1x_0$
- 对于0,根据补码的定义:
- $+0=+0_{n-1}...0_10_0$
- 此时正0的补码为$+0_{[补]}=0_n0_{n-1}...0_10_0$
- $-0=-0_{n-1}...0_10_0$
- 此时负0的补码为$-0_{[补]}=(10_n0_{n-1}...0_10_0-0_{n-1}...0_20_10_1)mod(10_n0_{n-1}...0_10_0)=0_n0_{n-1}...0_10_0$
由此可见,**零的补码是唯一的**,没有+0和-0之分。
- 对于负数$x=-x_{n-1}...x_1x_0$
常常可以通过把**数值位按位取反**,然后**末位加一来计算负数的补码**。
- 如求$-127$的补码
- $[-0111 1111]_{[补]}=10000 0000-01111111 $
- $10000000=11111111+1$
- $[-0111 1111]_{[补]}=11111111-01111111+1$,这一步刚刚说明了上面的计算方法的原理。
$-128$的补码的求法。
- -128=-1000 0000
- $[-10000000]_{[补]}=11111111-10000000+1=10000000$
其实还有一个更为渐变的补码的求法:**从右到左遇到第一个 1 的前面各位取反。**也就是从右向左,遇到1之前,还保持原样。遇到1之后,各位取反。以-126为例:$-126=-01111110$
[-01111110]的补码位**100000**10,10是不变的。而黑体部分则是取反的。
对于补码的取值范围,10000000-11111111——- $-128$~$-1$
00000000~011111111 ——0~127
推广到n位数,则**补码的范围**就是[$-2^{n-1},2^{n-1}-1$]
#### 定点小数
定点小数的补码形式为$x_s.x_1x_2...x_n$(**实际上小数点是不存储的**),其中$x_s$代表符号位。则补码的定义为:
$$
x_{[原]}=\left\{\begin{matrix}x & 0 \leqslant x<1 \\ 2+x=2-|x| & -1\leqslant x\leqslant0\end{matrix}\right.
$$
在上式中,x代表的是真值。
例如,$x=+0.875$,化为二进制表示为$x=+0.111$;$x_{[补]}=0.111$。
$x=-0.875$二进制表示为$x=-0.111$;$x_{[补]}=10.000-(0.111)=1.001$。
我们可以总结出来:
- 对于正数$x=+0.x_{n-1}...x_1x_0$,它的补码是它自己本身,常常在最高位前面补0,代表它是一个正数。(注意,**前面的0.实际上是不存储的**,也就是实际最高位是$x_{n-1}$)
- $x_{[原]}=0.x_{n-1}...x_1x_0$
- 对于0,根据补码的定义:
- $+0=+0.0_{n-1}...0_10_0$
- 此时正0的补码为$+0_{[补]}=0.0_{n-1}...0_10_0$
- $-0=-0.0_{n-1}...0_10_0$
- 此时负0的补码为$-0_{[补]}=(10.0_{n-1}...0_10_0-0.0_{n-1}...0_10_0)mod(10.0_{n-1}...0_10_0)=0.0_{n-1}...0_10_0$
也就是说**,0的补码是唯一的**。
- 对于负数
按位取反,末位加一,和定点整数一样。虽然我们看起来有一个小数点,但是实际上小数点是不存储的。
定点小数的补码的范围,0000~0111--> [0,0.875]
1000~1111--> [-1,-0.125]
扩展到n位补码
我们很容易求出它的范围$[-1,1-2^{-(n-1)}] $
#### 补码的运算
假设一个二进制整数补码有n+1位,$x_nx_{n-1}...x_2x_1x_0$,则补码与真值的对应关系可以这么表示:
$X_{真值}=-2^n\times x_n+\sum_{0}^{n-1}2^ix_n$
当该数为正整数的时候,$x_n$位变为0,$0x_{n-1}...x_2x_1x_0$,
$X_{真值}=\sum_{0}^{n-1}2^ix_n$
当该数为负整数的时候,$x_n$位变为1,$1 x_{n-1}...x_2x_1x_0$,
$X_{真值}=-2^n+\sum_{0}^{n-1}2^ix_n$
- 以-127为例,-127=-01111111
- 它的补码为10000001
- 从补码求真值的过程:-10000000+1=-01111111-1+1=-01111111
上面我们说到过,计算机中用原码进行加减运算是十分麻烦的,那么我们来看一下用补码来运算。
$126-127=0$
- 原码
- $01111110-01111111$
- 我们需要比较数值位的绝对值大小,来决定符号位,1
- 1111111-1111110=0000001
- 10000001
假设把减法看成加法
- 01111110+(-01111111)=01111110+11111111=**1**00000001
- 1会溢出,那么得到的结果就是00000001,按原码表示的化,真值为1,显然是错误的。
- 补码
- 01111110+10000001=11111111
- 转换为真值后为-1。正确的
- 原理是这样的
- 126-127=-1
- 126+(-127)=-1
- 126+129mod256=-1
- 这里-127等效于129mod256
由此,我们可以看出,补码实际上是**可以直接带符号位运算的运算**的。
求相反数的补码:**由[X]补求[-X]补**
**带符号位一起取反,然后末位加一**
如求我们**已知+127的补码求-127的补码**:
- 01111111
- 10000001
### 移码
移码通常用于表示浮点数的阶码。由于阶码是k位的整数,假设定点整数移码形式为$e_ke_{k-1}...e_2e_1e_0$最高位为符号位是。移码的传统定义是:
$[e]_移=2^k+e$
上式中,e为真值,$2^k$为固定的偏移值常数。
**与[x]补的区别:符号位相反**
| 真值 | 补码 | 移码 |
| ---- | ------ | ------- |
| -8 | 1000 | 0000 |
| -7 | 1001 | 0001 |
| -6 | 1002 | 0002 |
| …… | ...... | ...... |
| 0 | 0000 | 1000 |
| +1 | 0001 | 1001 |
| …… | ...... | ....... |
| +7 | 0111 | 1111 |
#### 移码的表示
移码表示的机器数为数的真值在数轴上向右平移了 固定的偏移值。
如八位移码:

#### 移码的特点
- 在移码中,最高位为0表示负数,最高位为1表示正数,这与**原 码、补码、反码的符号位取值正好相反**。
- 移码为全0时所对应的真值最小,为全1时所对应的真值最大! 因此,**移码的大小直观地反映了真值的大小,这将有助于两个 浮点数进行阶码大小比较**。
- 真值0在移码中的表示形式是**唯一**的,即:**[+0]移= [0]移= 100…00**
- 移码**把真值映射到一个正数域**,所以可将移码视为无符号数, 直接按无符号数规则比较大小。
- 同一数值的移码和补码除最高位相反外,其他各位相同。
### 原码、反码、补码、移码
取值范围的一个比较

 我们既可以顺时针调也可以逆时针调。也就是说我们$5-2$和$5+10$的效果是一样的。
而把这种思想引入到计算机中,不就可以把减法转为加法了吗?
$$
5-2=5+10(MOD 12) \\5+(-2)=5+10(MOD 12)\\ -2=10(MOD 12)
$$
在上面的式子中,在**模为12的情况下,-2的补码就是10**。一个负 数用其补码代替,同样可以得到正确的运算结果。
那什么是**模**呢?
> 计算机中运算器、寄存器、计数器都有一定的位数,不可能容纳无限大的任意数。当运算结果超出实际的最大表示范围, 就会发生溢出,此时所产生的**溢出量**就是**模(module)**
可以把模定义为一个**计量器的容量**。
如一个**八位计数器**,`0000 0000~1111 1111`,它表示的范围就是`[0,255]`。当计数器表示为`1111 1111` 时,如果**计数器再加一**,那么此计数器就会溢出。计数器上的数值会变成**0000 0000**.而此计数器的溢出量就是**256**.
假设此计数器表示一个定点小数,它表示的范围就是[0,2-$2^{-8}$]。当表示最大的时候,计数器值为**1.111 1111**当**计数器加一**的时候,那么计数器就会清零,变为**0.0000000**。那么此此定点小数的溢出量就是**2**.
从上面我们可以推导出,一个`n+1`位定点整数$x_n x_{(n-1)} ... x_2 x_1 x_0$,它的溢出量为$2^{n+1}$,所以模为$2^{n+1}$。
任意一个定点小数$x_s.x_1x_2...x_n$,它的溢出量是2,所以模为2。
而**在计算机中**,机器能表示的**数据位数是固定**的, 其**运算都是有模运算**。若运算结果**超出**了计算机所能表示的数值范围, 则只**保留它的小于模的低n+1位**的数值,**超过n+1 位**的高位部分就**自动舍弃**了。
下面我们来引入**补码的定义**:
#### 定点整数
定点整数的补码形式为$x_n x_{n-1}\cdot\cdot\cdot x_1x_0$,其中$x_n$为符号位,补码表示的定义为:
$$
x_{[补]}=\left\{\begin{matrix}x & 0 \leqslant x<2^n \\ 2^{n+1}+x=2^{n+1}-|x| & -2^n \leqslant x\leqslant0\end{matrix}\right.
$$
在上式中,**x代表的是真值**。
例如,$x=+7$,化为二进制表示为$x=+0111$;$x_{[补]}=0111$。
$x=-7$,化为二进制表示为$x=-0111$;$x_{[补]}=2^4+(-0111)=10000-0111=1001$。
我们可以总结出来:
- 对于正数$x=+x_{n-1}...x_1x_0$,它的补码是它自己本身,常常在最高位前面补0,代表它是一个正数。
- $x_{[补]}=0_nx_{n-1}...x_1x_0$
- 对于0,根据补码的定义:
- $+0=+0_{n-1}...0_10_0$
- 此时正0的补码为$+0_{[补]}=0_n0_{n-1}...0_10_0$
- $-0=-0_{n-1}...0_10_0$
- 此时负0的补码为$-0_{[补]}=(10_n0_{n-1}...0_10_0-0_{n-1}...0_20_10_1)mod(10_n0_{n-1}...0_10_0)=0_n0_{n-1}...0_10_0$
由此可见,**零的补码是唯一的**,没有+0和-0之分。
- 对于负数$x=-x_{n-1}...x_1x_0$
常常可以通过把**数值位按位取反**,然后**末位加一来计算负数的补码**。
- 如求$-127$的补码
- $[-0111 1111]_{[补]}=10000 0000-01111111 $
- $10000000=11111111+1$
- $[-0111 1111]_{[补]}=11111111-01111111+1$,这一步刚刚说明了上面的计算方法的原理。
$-128$的补码的求法。
- -128=-1000 0000
- $[-10000000]_{[补]}=11111111-10000000+1=10000000$
其实还有一个更为渐变的补码的求法:**从右到左遇到第一个 1 的前面各位取反。**也就是从右向左,遇到1之前,还保持原样。遇到1之后,各位取反。以-126为例:$-126=-01111110$
[-01111110]的补码位**100000**10,10是不变的。而黑体部分则是取反的。
对于补码的取值范围,10000000-11111111——- $-128$~$-1$
00000000~011111111 ——0~127
推广到n位数,则**补码的范围**就是[$-2^{n-1},2^{n-1}-1$]
#### 定点小数
定点小数的补码形式为$x_s.x_1x_2...x_n$(**实际上小数点是不存储的**),其中$x_s$代表符号位。则补码的定义为:
$$
x_{[原]}=\left\{\begin{matrix}x & 0 \leqslant x<1 \\ 2+x=2-|x| & -1\leqslant x\leqslant0\end{matrix}\right.
$$
在上式中,x代表的是真值。
例如,$x=+0.875$,化为二进制表示为$x=+0.111$;$x_{[补]}=0.111$。
$x=-0.875$二进制表示为$x=-0.111$;$x_{[补]}=10.000-(0.111)=1.001$。
我们可以总结出来:
- 对于正数$x=+0.x_{n-1}...x_1x_0$,它的补码是它自己本身,常常在最高位前面补0,代表它是一个正数。(注意,**前面的0.实际上是不存储的**,也就是实际最高位是$x_{n-1}$)
- $x_{[原]}=0.x_{n-1}...x_1x_0$
- 对于0,根据补码的定义:
- $+0=+0.0_{n-1}...0_10_0$
- 此时正0的补码为$+0_{[补]}=0.0_{n-1}...0_10_0$
- $-0=-0.0_{n-1}...0_10_0$
- 此时负0的补码为$-0_{[补]}=(10.0_{n-1}...0_10_0-0.0_{n-1}...0_10_0)mod(10.0_{n-1}...0_10_0)=0.0_{n-1}...0_10_0$
也就是说**,0的补码是唯一的**。
- 对于负数
按位取反,末位加一,和定点整数一样。虽然我们看起来有一个小数点,但是实际上小数点是不存储的。
定点小数的补码的范围,0000~0111--> [0,0.875]
1000~1111--> [-1,-0.125]
扩展到n位补码
我们很容易求出它的范围$[-1,1-2^{-(n-1)}] $
#### 补码的运算
假设一个二进制整数补码有n+1位,$x_nx_{n-1}...x_2x_1x_0$,则补码与真值的对应关系可以这么表示:
$X_{真值}=-2^n\times x_n+\sum_{0}^{n-1}2^ix_n$
当该数为正整数的时候,$x_n$位变为0,$0x_{n-1}...x_2x_1x_0$,
$X_{真值}=\sum_{0}^{n-1}2^ix_n$
当该数为负整数的时候,$x_n$位变为1,$1 x_{n-1}...x_2x_1x_0$,
$X_{真值}=-2^n+\sum_{0}^{n-1}2^ix_n$
- 以-127为例,-127=-01111111
- 它的补码为10000001
- 从补码求真值的过程:-10000000+1=-01111111-1+1=-01111111
上面我们说到过,计算机中用原码进行加减运算是十分麻烦的,那么我们来看一下用补码来运算。
$126-127=0$
- 原码
- $01111110-01111111$
- 我们需要比较数值位的绝对值大小,来决定符号位,1
- 1111111-1111110=0000001
- 10000001
假设把减法看成加法
- 01111110+(-01111111)=01111110+11111111=**1**00000001
- 1会溢出,那么得到的结果就是00000001,按原码表示的化,真值为1,显然是错误的。
- 补码
- 01111110+10000001=11111111
- 转换为真值后为-1。正确的
- 原理是这样的
- 126-127=-1
- 126+(-127)=-1
- 126+129mod256=-1
- 这里-127等效于129mod256
由此,我们可以看出,补码实际上是**可以直接带符号位运算的运算**的。
求相反数的补码:**由[X]补求[-X]补**
**带符号位一起取反,然后末位加一**
如求我们**已知+127的补码求-127的补码**:
- 01111111
- 10000001
### 移码
移码通常用于表示浮点数的阶码。由于阶码是k位的整数,假设定点整数移码形式为$e_ke_{k-1}...e_2e_1e_0$最高位为符号位是。移码的传统定义是:
$[e]_移=2^k+e$
上式中,e为真值,$2^k$为固定的偏移值常数。
**与[x]补的区别:符号位相反**
| 真值 | 补码 | 移码 |
| ---- | ------ | ------- |
| -8 | 1000 | 0000 |
| -7 | 1001 | 0001 |
| -6 | 1002 | 0002 |
| …… | ...... | ...... |
| 0 | 0000 | 1000 |
| +1 | 0001 | 1001 |
| …… | ...... | ....... |
| +7 | 0111 | 1111 |
#### 移码的表示
移码表示的机器数为数的真值在数轴上向右平移了 固定的偏移值。
如八位移码:

#### 移码的特点
- 在移码中,最高位为0表示负数,最高位为1表示正数,这与**原 码、补码、反码的符号位取值正好相反**。
- 移码为全0时所对应的真值最小,为全1时所对应的真值最大! 因此,**移码的大小直观地反映了真值的大小,这将有助于两个 浮点数进行阶码大小比较**。
- 真值0在移码中的表示形式是**唯一**的,即:**[+0]移= [0]移= 100…00**
- 移码**把真值映射到一个正数域**,所以可将移码视为无符号数, 直接按无符号数规则比较大小。
- 同一数值的移码和补码除最高位相反外,其他各位相同。
### 原码、反码、补码、移码
取值范围的一个比较

我们既可以顺时针调也可以逆时针调。也就是说我们$5-2$和$5+10$的效果是一样的。
而把这种思想引入到计算机中,不就可以把减法转为加法了吗?
$$
5-2=5+10(MOD 12) \\5+(-2)=5+10(MOD 12)\\ -2=10(MOD 12)
$$
在上面的式子中,在**模为12的情况下,-2的补码就是10**。一个负 数用其补码代替,同样可以得到正确的运算结果。
那什么是**模**呢?
> 计算机中运算器、寄存器、计数器都有一定的位数,不可能容纳无限大的任意数。当运算结果超出实际的最大表示范围, 就会发生溢出,此时所产生的**溢出量**就是**模(module)**
可以把模定义为一个**计量器的容量**。
如一个**八位计数器**,`0000 0000~1111 1111`,它表示的范围就是`[0,255]`。当计数器表示为`1111 1111` 时,如果**计数器再加一**,那么此计数器就会溢出。计数器上的数值会变成**0000 0000**.而此计数器的溢出量就是**256**.
假设此计数器表示一个定点小数,它表示的范围就是[0,2-$2^{-8}$]。当表示最大的时候,计数器值为**1.111 1111**当**计数器加一**的时候,那么计数器就会清零,变为**0.0000000**。那么此此定点小数的溢出量就是**2**.
从上面我们可以推导出,一个`n+1`位定点整数$x_n x_{(n-1)} ... x_2 x_1 x_0$,它的溢出量为$2^{n+1}$,所以模为$2^{n+1}$。
任意一个定点小数$x_s.x_1x_2...x_n$,它的溢出量是2,所以模为2。
而**在计算机中**,机器能表示的**数据位数是固定**的, 其**运算都是有模运算**。若运算结果**超出**了计算机所能表示的数值范围, 则只**保留它的小于模的低n+1位**的数值,**超过n+1 位**的高位部分就**自动舍弃**了。
下面我们来引入**补码的定义**:
#### 定点整数
定点整数的补码形式为$x_n x_{n-1}\cdot\cdot\cdot x_1x_0$,其中$x_n$为符号位,补码表示的定义为:
$$
x_{[补]}=\left\{\begin{matrix}x & 0 \leqslant x<2^n \\ 2^{n+1}+x=2^{n+1}-|x| & -2^n \leqslant x\leqslant0\end{matrix}\right.
$$
在上式中,**x代表的是真值**。
例如,$x=+7$,化为二进制表示为$x=+0111$;$x_{[补]}=0111$。
$x=-7$,化为二进制表示为$x=-0111$;$x_{[补]}=2^4+(-0111)=10000-0111=1001$。
我们可以总结出来:
- 对于正数$x=+x_{n-1}...x_1x_0$,它的补码是它自己本身,常常在最高位前面补0,代表它是一个正数。
- $x_{[补]}=0_nx_{n-1}...x_1x_0$
- 对于0,根据补码的定义:
- $+0=+0_{n-1}...0_10_0$
- 此时正0的补码为$+0_{[补]}=0_n0_{n-1}...0_10_0$
- $-0=-0_{n-1}...0_10_0$
- 此时负0的补码为$-0_{[补]}=(10_n0_{n-1}...0_10_0-0_{n-1}...0_20_10_1)mod(10_n0_{n-1}...0_10_0)=0_n0_{n-1}...0_10_0$
由此可见,**零的补码是唯一的**,没有+0和-0之分。
- 对于负数$x=-x_{n-1}...x_1x_0$
常常可以通过把**数值位按位取反**,然后**末位加一来计算负数的补码**。
- 如求$-127$的补码
- $[-0111 1111]_{[补]}=10000 0000-01111111 $
- $10000000=11111111+1$
- $[-0111 1111]_{[补]}=11111111-01111111+1$,这一步刚刚说明了上面的计算方法的原理。
$-128$的补码的求法。
- -128=-1000 0000
- $[-10000000]_{[补]}=11111111-10000000+1=10000000$
其实还有一个更为渐变的补码的求法:**从右到左遇到第一个 1 的前面各位取反。**也就是从右向左,遇到1之前,还保持原样。遇到1之后,各位取反。以-126为例:$-126=-01111110$
[-01111110]的补码位**100000**10,10是不变的。而黑体部分则是取反的。
对于补码的取值范围,10000000-11111111——- $-128$~$-1$
00000000~011111111 ——0~127
推广到n位数,则**补码的范围**就是[$-2^{n-1},2^{n-1}-1$]
#### 定点小数
定点小数的补码形式为$x_s.x_1x_2...x_n$(**实际上小数点是不存储的**),其中$x_s$代表符号位。则补码的定义为:
$$
x_{[原]}=\left\{\begin{matrix}x & 0 \leqslant x<1 \\ 2+x=2-|x| & -1\leqslant x\leqslant0\end{matrix}\right.
$$
在上式中,x代表的是真值。
例如,$x=+0.875$,化为二进制表示为$x=+0.111$;$x_{[补]}=0.111$。
$x=-0.875$二进制表示为$x=-0.111$;$x_{[补]}=10.000-(0.111)=1.001$。
我们可以总结出来:
- 对于正数$x=+0.x_{n-1}...x_1x_0$,它的补码是它自己本身,常常在最高位前面补0,代表它是一个正数。(注意,**前面的0.实际上是不存储的**,也就是实际最高位是$x_{n-1}$)
- $x_{[原]}=0.x_{n-1}...x_1x_0$
- 对于0,根据补码的定义:
- $+0=+0.0_{n-1}...0_10_0$
- 此时正0的补码为$+0_{[补]}=0.0_{n-1}...0_10_0$
- $-0=-0.0_{n-1}...0_10_0$
- 此时负0的补码为$-0_{[补]}=(10.0_{n-1}...0_10_0-0.0_{n-1}...0_10_0)mod(10.0_{n-1}...0_10_0)=0.0_{n-1}...0_10_0$
也就是说**,0的补码是唯一的**。
- 对于负数
按位取反,末位加一,和定点整数一样。虽然我们看起来有一个小数点,但是实际上小数点是不存储的。
定点小数的补码的范围,0000~0111--> [0,0.875]
1000~1111--> [-1,-0.125]
扩展到n位补码
我们很容易求出它的范围$[-1,1-2^{-(n-1)}] $
#### 补码的运算
假设一个二进制整数补码有n+1位,$x_nx_{n-1}...x_2x_1x_0$,则补码与真值的对应关系可以这么表示:
$X_{真值}=-2^n\times x_n+\sum_{0}^{n-1}2^ix_n$
当该数为正整数的时候,$x_n$位变为0,$0x_{n-1}...x_2x_1x_0$,
$X_{真值}=\sum_{0}^{n-1}2^ix_n$
当该数为负整数的时候,$x_n$位变为1,$1 x_{n-1}...x_2x_1x_0$,
$X_{真值}=-2^n+\sum_{0}^{n-1}2^ix_n$
- 以-127为例,-127=-01111111
- 它的补码为10000001
- 从补码求真值的过程:-10000000+1=-01111111-1+1=-01111111
上面我们说到过,计算机中用原码进行加减运算是十分麻烦的,那么我们来看一下用补码来运算。
$126-127=0$
- 原码
- $01111110-01111111$
- 我们需要比较数值位的绝对值大小,来决定符号位,1
- 1111111-1111110=0000001
- 10000001
假设把减法看成加法
- 01111110+(-01111111)=01111110+11111111=**1**00000001
- 1会溢出,那么得到的结果就是00000001,按原码表示的化,真值为1,显然是错误的。
- 补码
- 01111110+10000001=11111111
- 转换为真值后为-1。正确的
- 原理是这样的
- 126-127=-1
- 126+(-127)=-1
- 126+129mod256=-1
- 这里-127等效于129mod256
由此,我们可以看出,补码实际上是**可以直接带符号位运算的运算**的。
求相反数的补码:**由[X]补求[-X]补**
**带符号位一起取反,然后末位加一**
如求我们**已知+127的补码求-127的补码**:
- 01111111
- 10000001
### 移码
移码通常用于表示浮点数的阶码。由于阶码是k位的整数,假设定点整数移码形式为$e_ke_{k-1}...e_2e_1e_0$最高位为符号位是。移码的传统定义是:
$[e]_移=2^k+e$
上式中,e为真值,$2^k$为固定的偏移值常数。
**与[x]补的区别:符号位相反**
| 真值 | 补码 | 移码 |
| ---- | ------ | ------- |
| -8 | 1000 | 0000 |
| -7 | 1001 | 0001 |
| -6 | 1002 | 0002 |
| …… | ...... | ...... |
| 0 | 0000 | 1000 |
| +1 | 0001 | 1001 |
| …… | ...... | ....... |
| +7 | 0111 | 1111 |
#### 移码的表示
移码表示的机器数为数的真值在数轴上向右平移了 固定的偏移值。
如八位移码:

#### 移码的特点
- 在移码中,最高位为0表示负数,最高位为1表示正数,这与**原 码、补码、反码的符号位取值正好相反**。
- 移码为全0时所对应的真值最小,为全1时所对应的真值最大! 因此,**移码的大小直观地反映了真值的大小,这将有助于两个 浮点数进行阶码大小比较**。
- 真值0在移码中的表示形式是**唯一**的,即:**[+0]移= [0]移= 100…00**
- 移码**把真值映射到一个正数域**,所以可将移码视为无符号数, 直接按无符号数规则比较大小。
- 同一数值的移码和补码除最高位相反外,其他各位相同。
### 原码、反码、补码、移码
取值范围的一个比较

加载全部内容