分治法-凸包问题

时间:2020-03-17 Swithun 人气:4

什么是凸包？

我的理解就是，图形任意两点的连线都没有在图形外部。

问题：给定点集，怎么求出凸包的边界点呢？？？

第一步：给这些点按照X的从大到小进行排序，如果X相同的按照Y再排序。

第二步：把X最小的和最大的连起来，他们必为凸包的边界点。

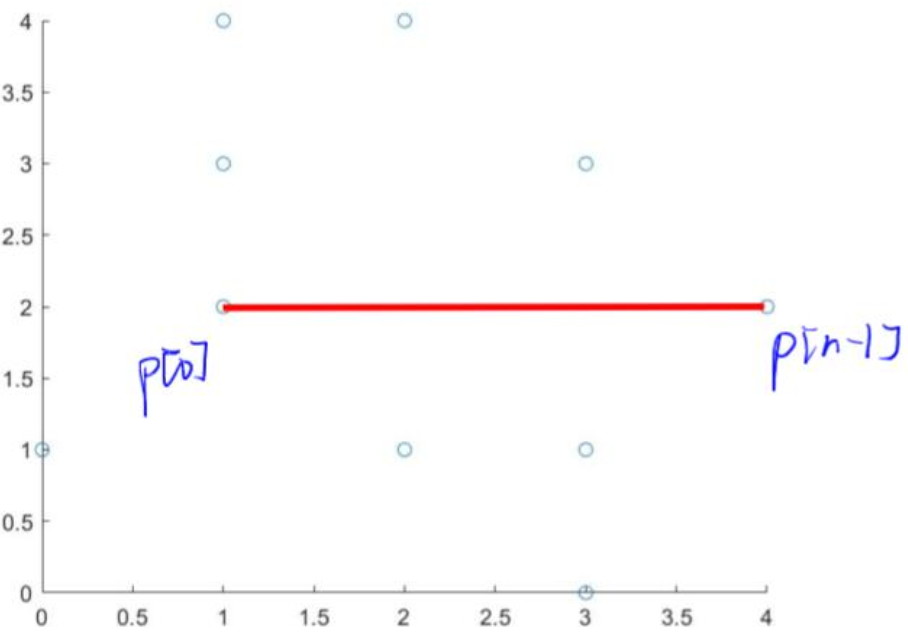
第三步：把平面区域分为两个部分，分别在上面和下面去找面积最大的三角形（面积最大包括的点也就越多嘛，所以适合当凸包的边界点）

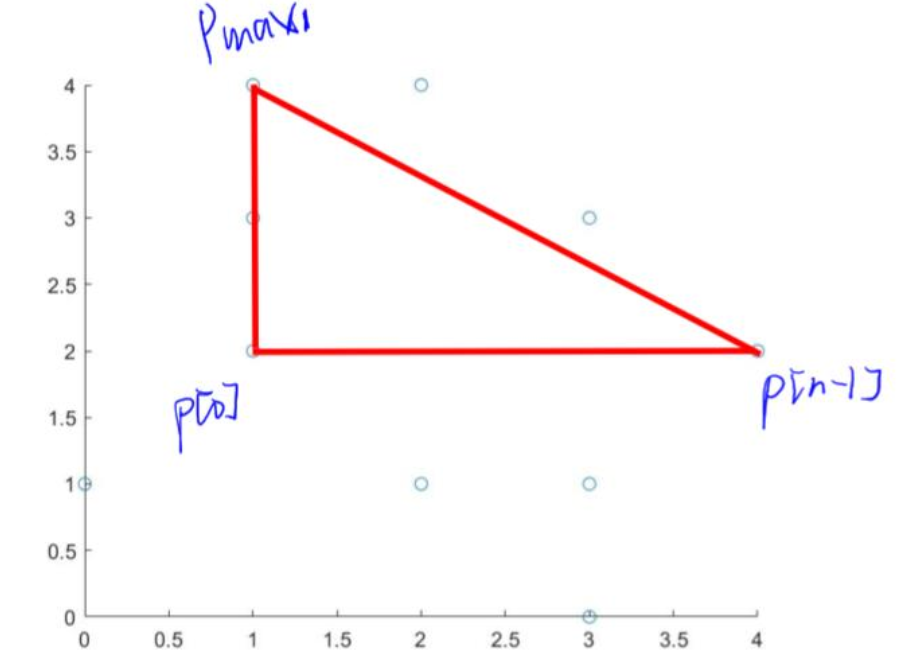
那面积怎么求呢？

求三角形的面积，假设三个点，A(x1,y1),B(x2,y2), C(x3,y3)，以下行列式对于平面上任意三角形, 求解面积都很方便, 所得结果是三角形ABC面积的两倍，A->B->C为顺时针顺序时，该值为正,，反之则为负。

第四步：进行递归，把三角形左边那个边作为底边又去找面积最大的三角形，同理右边，下面也一样。

上代码！！！

#include <iostream>
using namespace std;
#include <algorithm>
#include <stdlib.h>
#define N 10000
int n = 0;
struct POINT
{
    int x, y;
}p[N],ans[N];
int visit[N],mark[N];
int Djudge(POINT a1, POINT a2, POINT a3)
{
    int calculate = a1.x*a2.y + a3.x*a1.y + a2.x*a3.y - a3.x*a2.y - a2.x*a1.y - a1.x*a3.y;
    return calculate;
}
bool cmpxy(const POINT a, const POINT b) //按x轴排序,如果x相同,按y轴排序
{
    if (a.x != b.x)
        return a.x < b.x;
    else
        return a.y < b.y;
}
void DealLeft(int first, int last)
{
    int max = 0, index = -1;
    int i = first;
    if (first < last)
    {
        for (i = first+1; i < last; i++) //注意两端,对于first和last,没必要再进行计算
        {
            int calcu = Djudge(p[first], p[i], p[last]);
            if (calcu == 0) {  visit[i] = 1; } //
            if (calcu > max)
            {
                max = calcu;
                index = i;
            }
 
        }
    }
    else
    {
        for (i-1; i >last; i--) //如果first>last,重复上述过程,注意这里下界不是0.
        {
            int calcu = Djudge(p[first], p[i], p[last]);
            if (calcu == 0) {visit[i] = 1;} //
            if (calcu >  max)
            {
                max = calcu;
                index = i;
            }
        }
    }
    if (index != -1)
    {
        visit[index] = 1; //对取到的点进行标注  
        DealLeft(first, index);
        DealLeft(index, last);//分治的部分
    }
}
 
int main()
{
	cout<<"请输入点数："<<endl;
    cin >> n;
	cout<<"请输入点的坐标："<<endl;
    for (int i = 0; i < n; i++)
    {
        cin >> p[i].x >> p[i].y;
        visit[i] = 0;
    }
    visit[0] = 1;
    visit[n - 1] = 1;
    sort(p, p + n, cmpxy);
    DealLeft(0, n - 1); //查找上凸包;
    DealLeft(n - 1, 0); //查找下凸包;
    int t = 0;
    for (int i = 0; i < n; i++)
    {
        if (visit[i] == 1)
        {
            ans[t].x = p[i].x;
            ans[t].y = p[i].y;
            t++;
        }
    }
//顺时针输出
    mark[0] = mark[t - 1] = 1; //数组mark避免重复检查降低效率
    for (int i = 1; i < t - 1; i++)
    {
        mark[i] = 0;
    }
	cout<<"凸包点的坐标："<<endl;
    cout << ans[0].x << " " <<ans[0].y<< endl;
    for (int i =1; i < t-1; i++)
    {
        int d = Djudge(ans[0], ans[t-1], ans[i]);
        if (d >= 0)
        {
            cout << ans[i].x << " " << ans[i].y << endl;
            mark[i] = 1;
        }
    }
    cout << ans[t - 1].x << " " << ans[t - 1].y << endl;
    for (int i = 1; i < t; i++)
    {
        if (mark[i] != 1)
        {
            int d = Djudge(ans[0], ans[t - 1], ans[i]);
            if (d < 0)
            {
                cout << ans[i].x << " " << ans[i].y << endl;
            }
        }
    }
    return 0;
}

加载全部内容