数据挖掘入门系列教程（四点五）之Apriori算法

[TOC] ## 数据挖掘入门系列教程（四点五）之Apriori算法 Apriori（先验）算法**关联规则**学习的经典算法之一，用来寻找出数据集中频繁出现的数据集合。如果看过以前的博客，是不是想到了这个跟[数据挖掘入门系列教程（一）之亲和性分析](https://www.cnblogs.com/xiaohuiduan/p/12419410.html)这篇博客很相似？Yes，的确很相似，只不过在这篇博客中，我们会更加深入的分析如何寻找可靠有效的亲和性。并在下一篇博客中使用Apriori算法去分析电影中的亲和性。这篇主要是介绍Apriori算法的流程。 ### 频繁（项集）数据的评判标准 这个在[数据挖掘入门系列教程（一）之亲和性分析](https://www.cnblogs.com/xiaohuiduan/p/12419410.html)这篇博客曾经提过，但在这里再重新详细的说一下。 何如判断一个数据是否是频繁？按照我们的想法，肯定是数据在数据集中出现次数的越多，则代表着这个数据出现的越频繁。 > 值得注意的是：在这里的数据可以是一个数据，也可以是多个数据 （项集）。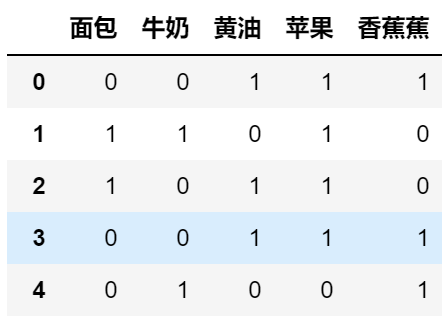 以下面这张图为例子，这张图每一列代表商品是否被购买（1代表被购买，0代表否），每一行代表一次交易记录：  常用的评估标准由**支持度**、**置信度**、和**提升度**三个： #### 支持度（support）: 支持度就是数据在数据集中出现的次数（也可以是次数占总数据集的比重），或者说其在数据集中出现的概率： 下面的公式以所占比例来说明： $$ \begin{split} & 如果是一个数据X，则其支持度为：\\ & support(X) = P(X) = \frac{num(X)}{num(ALL)} \\ & 如果数据是一个数据项集（X,Y）,则支持度为：\\ & support(X,Y) = P(X,Y) = \frac{num(XY)}{num(ALL)}\\ & 如果数据是一个数据项集（X,Y,Z）,则支持度为：\\ & support(X,Y,Z) = P(X,Y,Z) = \frac{num(XYZ)}{num(ALL)}\\ & (X,Y,Z代表的是X,Y,Z同时出现的次数) \end{split} $$ 以上面的交易为例： 我们来求 *（黄油，苹果）* 的支持度： *（黄油，苹果）* 在第`0，2，3`中通过出现了，一共是5条数据，因此$support(黄油,苹果) = \frac{3}{5} = 0.6$ > 一般来说，支持度高的不一定数据频繁，但是数据频繁的一定支持度高 #### 置信度（confidence）： 置信度代表的规则应验的准确性，也就是一个数据出现后，另外一个数据出现的概率，也就是条件概率。(以购买为例，就是已经购买Y的条件下，购买X的概率)公式如下： $$ \begin{split} & 设分析的数据是X,Y，则X对Y的置信度为：\\ & confidence(X \Leftarrow Y) = P(X|Y) = \frac{P(XY)}{P(Y)} \\ & 设分析的数据是X,Y,Z，则X对Y和Z的置信度为：\\ & confidence(X \Leftarrow YZ) = P(X|YZ) = \frac{P(XYZ)}{P(YZ)} \\ \end{split} $$ 还是以 *（黄油，苹果）* 为例子，计算黄油对苹果的置信度：$confidence(黄油\Leftarrow苹果) = \frac{3}{4} = 0.75$。 但是置信度有一个缺点，那就是它可能会扭曲关联的重要性。因为它只反应了Y的受欢迎的程度。如果X的受欢迎程度也很高的话，那么confidence也会很大。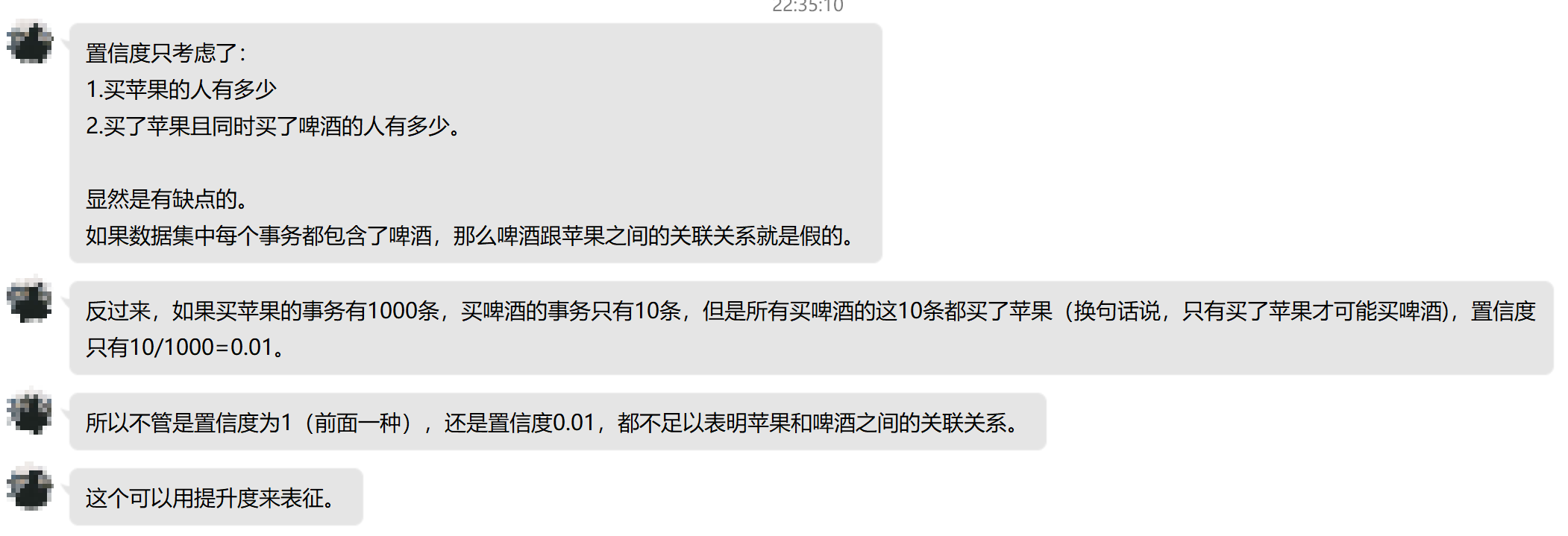下面是数据挖掘蒋少华老师的一段为什么我们需要使用`提升度`的话：  #### 提升度（Lift）： 提升度表示在含有Y的条件下，同时含有X的概率，同时考虑到X的概率，公式如下： $$ \begin{equation} \begin{aligned} Lift(X \Leftarrow Y) &= \frac{support(X,Y)}{support(X) \times support(Y)} \ \ &= \frac{P(X,Y)}{P(X) \times P(Y)}\\ & = \frac{P(X|Y)}{P(X)}\\ & = \frac{confidenc(X\Leftarrow Y)}{P(X)} \end{aligned} \end{equation} $$ 在提升度中，如果$Lift(X \Leftarrow Y) = 1$则表示X，Y之间相互独立，没有关联（因为$P(X|Y) = P(X)$），如果$Lift(X \Leftarrow Y) > 1$则表示$X \Leftarrow Y$则表示$X \Leftarrow Y$是有效的强关联（在购买Y的情况下很可能购买X）；如果$Lift(X \Leftarrow Y) < 1$则表示$X \Leftarrow Y$则表示$X \Leftarrow Y$是无效的强关联。 > 一般来说，我们如何判断一个数据集中数据的频繁程度时使用提升度来做的。 ### Apriori 算法流程 说完评判标准，接下来我们说一下算法的流程（来自参考1）。 > Apriori算法的目标是找到最大的K项频繁集。这里有两层意思，首先，我们要找到符合支持度标准（置信度or提升度）的频繁集。但是这样的频繁集可能有很多。第二层意思就是我们要找到最大个数的频繁集。比如我们找到符合支持度的频繁集AB和ABE，那么我们会抛弃AB，只保留ABE，因为AB是2项频繁集，而ABE是3项频繁集。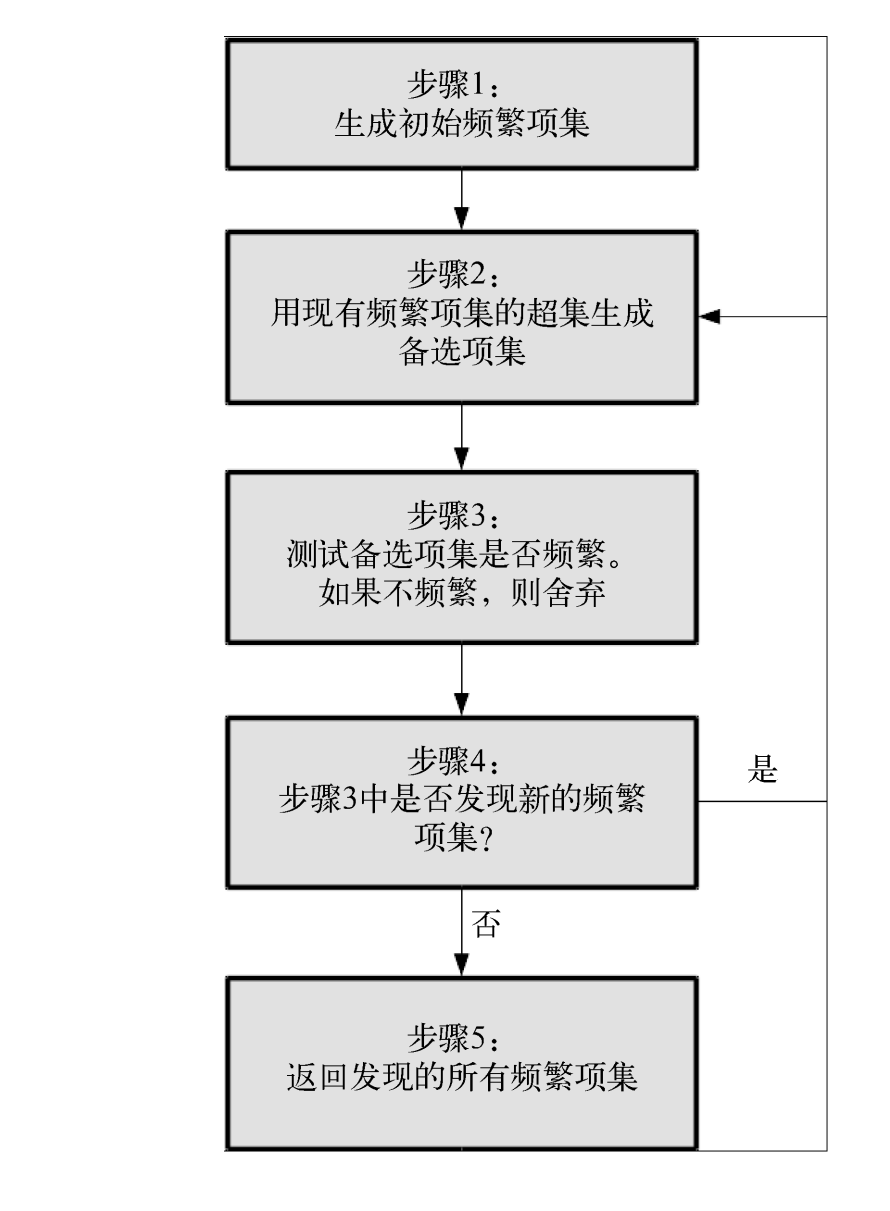 算法的流程图如下（图来自《Python数据挖掘入门与实践》）：  下面是一个具体的例子来介绍（图源不知道来自哪里，很多博客都在用），这个例子是以support作为评判标准，在图中$C_n$代表的是**备选项集**，L代表的是被剪掉后的选项集，$Min\ support = 50\%$代表的是最小符合标准的支持度（大于它则表示频繁）。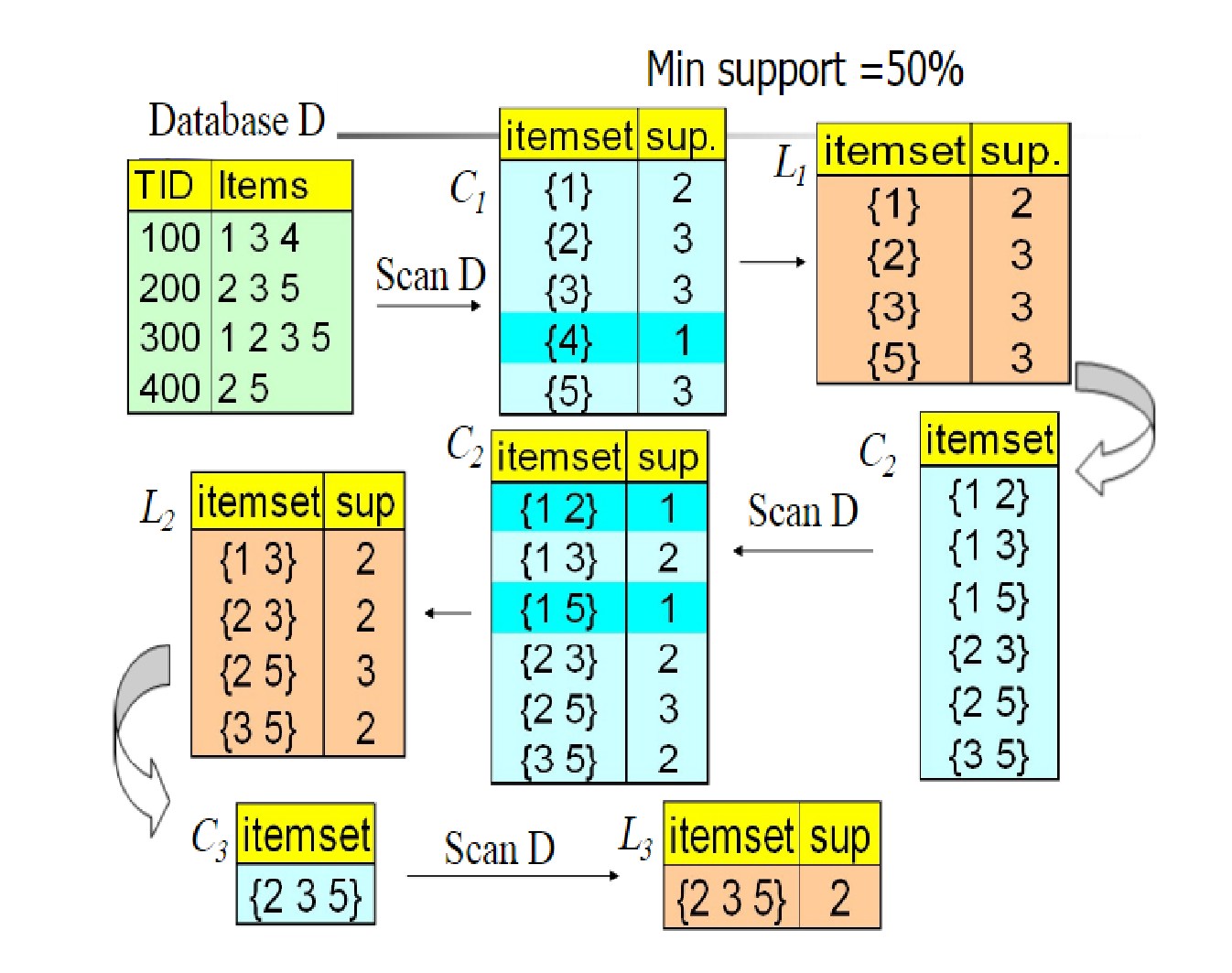  这个例子的图像还是满生动的，很容易看的懂。下面就简单的解释一下： 首先我们有数据集D，然后生成数据项$K =1$的备选项集$C_1$，然后去除$support_n < Min\ support$的数据项，得到$L_1$，然后又生成数据项$K =2$的备选项集$C_2$，然后又去除$support_n < Min\ support$的数据项。进行递归，直到无法发现新的频繁项。 ### 结尾 总的来说，Apriori算法不是很难，算法的流程也很简单，而它的核心在于如何构建一个有效的评判标准，support？confidence？Lift？or others？但是它也有一些缺点：每次递归都需要产生大量的备选项集，如果数据集很大的话，怎么办？重复的扫描数据集…… 在下一篇博客中，我将介绍如何使用Apriori算法对电影的数据集进行分析，然后找出之间的相关关系。 #### 参考 > 1. [Apriori算法原理总结](https://www.cnblogs.com/pinard/p/6293298.html) > 2. [Association Rules and the Apriori Algorithm: A Tutorial](https://www.kdnuggets.com/2016/04/association-rules-apriori-algorithm-tutorial.html) > 3. 《Python数据挖掘入门与实践》 > 4. 数据挖掘蒋少华老师