CTR学习笔记&代码实现1-深度学习的前奏LR->FFM

CTR学习笔记系列的第一篇，总结在深度模型称王之前经典LR，FM, FFM模型，这些经典模型后续也作为组件用于各个深度模型。模型分别用自定义Keras Layer和estimator来实现，哈哈一个是旧爱一个是新欢。特征工程依赖feature_column实现，这里做的比较简单在后面的深度模型再好好搞。完整代码在这里https://github.com/DSXiangLi/CTR ## 问题定义 CTR本质是一个二分类问题，$X \in R^N $是用户和广告相关特征, $Y \in (0,1)$是每个广告是否被点击，基础模型就是一个简单的Logistics Regression $$ P(Y=1) = \frac{1}{1+ exp{(w_0 + \sum_{i=1}^Nw_ix_i)}} $$ 考虑在之后TF框架里logistics可以简单用activation来表示，我们把核心的部分简化为以下 $$ y(x) = w_0 + \sum_{i=1}^Nw_ix_i $$

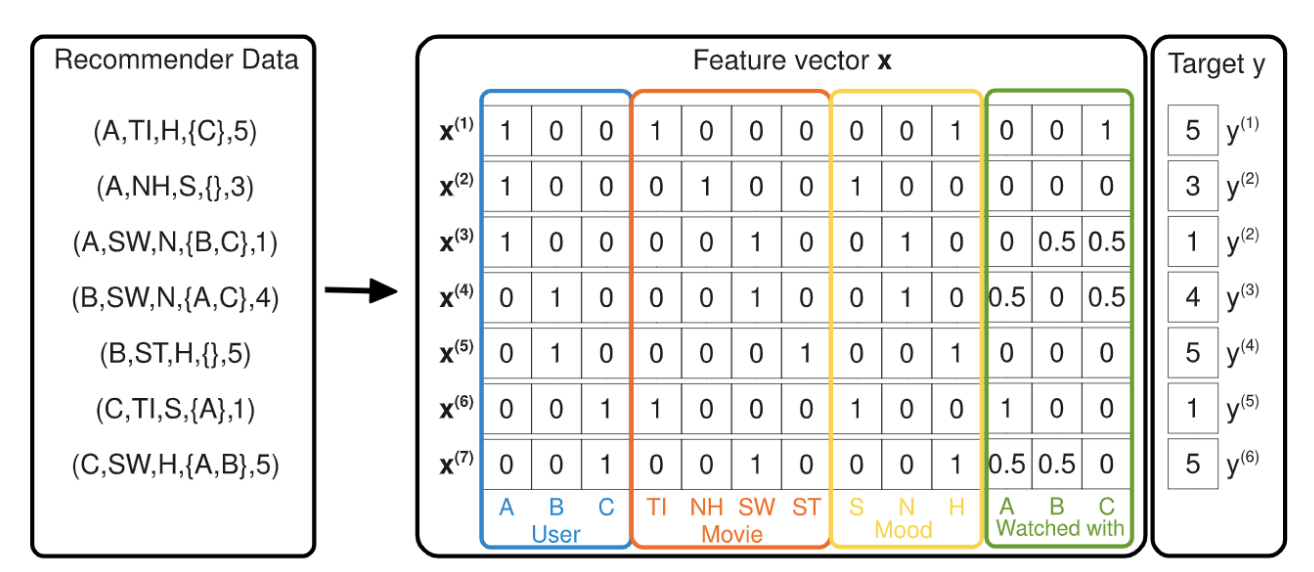
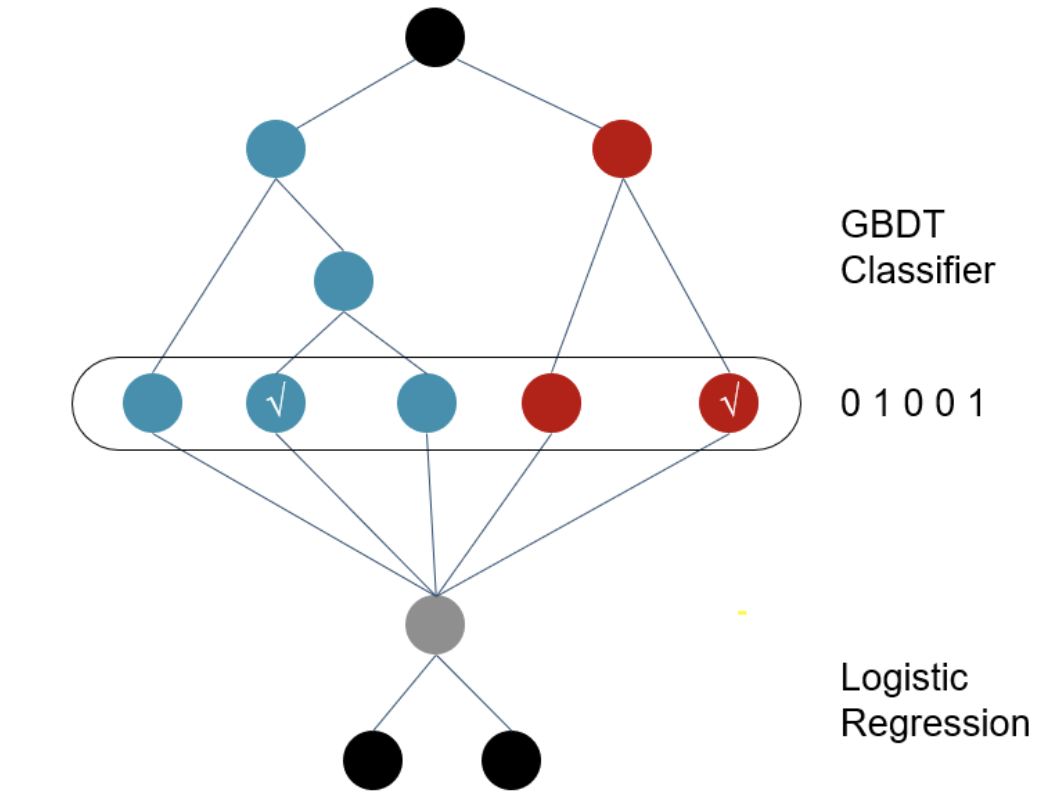
## LR模型 2010年之前主流的CTR模型通常是最简单的logistics regression，模型可解释性强，工程上部署简单快捷。但最大的问题是依赖于大量的手工特征工程。 刚接触特征工程的同学可能会好奇为什么需要计算组合特征？ 最开始我只是简单认为越细粒度的聚合特征Bias越小。接触了因果推理后，我觉得更适合用**Simpson Paradox**里的**Confounder Bias**来解释，不同聚合特征之间可能会相悖，例如各个年龄段的男性点击率均低于女性，但整体上男性的点击率高于女性。感兴趣的可以看看这篇博客[因果推理的春天系列序 - 数据挖掘中的Confounding, Collidar, Mediation Bias][1] 如果即想简化特征工程，又想加入特征组合，肯定就会想到下面的暴力特征组合方式。这个也被称作POLY2模型 $$ y(x) = w_0 + \sum_{i=1}^N w_ix_i + \sum_{i=1}^N \sum_{j=i+1}^N w_{i,j} x_ix_j $$ 但上述$w_{i,j}$需要学习$\frac{n(n-1)}{2}$个参数，一方面复杂度高，另一方面对高维稀疏特征会出现大量$w_{i,j}$是0的情况，模型无法学到样本中未曾出现的特征组合pattern，模型泛化性差。 于是**降低复杂度，自动选择有效特征组合，以及模型泛化**这三点成为后续主要的改进的方向。 ## GBDT+LR模型 2014年Facebook提出在GBDT叠加LR的方法，敲开了**特征工程模型化**的大门。GBDT输出的不是预测概率，而是每一个样本落在每一颗子树哪个叶节点的一个0/1矩阵。在只保留和target相关的有效特征组合的同时，避免了手工特征组合需要的业务理解和人工成本。 相较特征组合，我更喜欢把GBDT输出的特征向量，理解为根据target，对样本进行了聚类/降维，输出的是该样本所属的几个特定人群组合，每一棵子树都对应一种类型的人群组合。 但是！GBDT依旧存在泛化问题，因为所有叶节点的选择都依赖于训练样本，并且GBDT在离散特征上效果比较有限。同时也存在经过GBDT变换得到的特征依旧是高维稀疏特征的问题。

## FM模型 2010年Rendall提出的因子分解机模型(FM)为降低计算复杂度，为增加模型泛化能力提供了思路 ### 原理 FM模型将上述暴力特征组合直接求解整个权重矩$w_ij \in R^{N*N}$，转化为求解权重矩阵的隐向量$V \in R^{N*k}$，这一步会大大增加模型泛化能力，因为权重矩阵不再完全依赖于样本中的特定特征组合，而是可以通过特征间的相关关系间接得到。 同时隐向量把模型需要学习的参数数量从$\frac{n(n-1)}{2}$降低到$nk$个 $$ \begin{align} y(x) & = w_0 + \sum_{i=1}^Nw_i x_i + \sum_{i=1}^N \sum_{j=i+1}^N w_{i,j} x_ix_j\\ &= w_0 + \sum_{i=1}^Nw_i x_i + \sum_{i=1}^N \sum_{j=i+1}^N