【推荐算法工程师技术栈系列】推荐系统--热榜召回

[TOC] ## 排名公式 ### Hacker News(帖子投票) $$ score = \frac{(P-1)}{(T+2)^G} $$ $其中P = 文章获得的票数( -1 是去掉文章提交人的票)$ $T = 从文章提交至今的时间(小时)$ $G = 比重，news.arc里缺省值是1.8$  ### Reddit(帖子赞踩) $$ f(t_s, y, z)=\log_{10} z+\frac{y t_{s}}{45000} $$ $其中t_{s}是发帖时间据网站成立的时间$ $y 是一个符号变量，表示对文章的总体看法。如果赞成票居多，y就是 +1；如果反对票居多，y就是-1；如果赞成票和反对票相等，y就是0。$ $z 表示赞成票超过反对票的数量。如果赞成票少于或等于反对票，那么z就等于1。$ 这种算法的一个问题是，对于那些有争议的文章（赞成票和反对票非常接近），它们不可能排到前列。假定同一时间有两个帖子发表，文章A有 1 张赞成票（发帖人投的）、0张反对票，文章B有 1000 张赞成票、1000张反对票，那么A的排名会高于B，这显然不合理。 　　结论就是，Reddit 的排名，基本上由发帖时间决定，超级受欢迎的文章会排在最前面，一般性受欢迎的文章、有争议的文章都不会很靠前。这决定了 Reddit 是一个符合大众口味的社区，不是一个很激进、可以展示少数派想法的地方。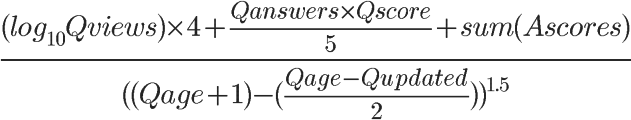 ### Stack Overflow(问题的得分、回答的数目和该问题的浏览次数)  1）Qviews（问题的浏览次数） 某个问题的浏览次数越多，就代表越受关注，得分也就越高。这里使用了以 10 为底的对数，用意是当访问量越来越大，它对得分的影响将不断变小。 2）Qscore（问题得分）和 Qanswers（回答的数量） 　　首先，Qscore（问题得分）= 赞成票-反对票。如果某个问题越受到好评，排名自然应该越靠前。 　　Qanswers 表示回答的数量，代表有多少人参与这个问题。这个值越大，得分将成倍放大。这里需要注意的是，如果无人回答，Qanswers 就等于0，这时 Qscore 再高也没用，意味着再好的问题，也必须有人回答，否则进不了热点问题排行榜。 3）Ascores（回答得分） 　　一般来说，"回答"比"问题"更有意义。这一项的得分越高，就代表回答的质量越高。 　　但是我感觉，简单加总的设计还不够全面。这里有两个问题。首先，一个正确的回答胜过一百个无用的回答，但是，简单加总会导致，1个得分为 100 的回答与 100 个得分为 1 的回答，总得分相同。其次，由于得分会出现负值，因此那些特别差的回答，会拉低正确回答的得分。 4）Qage（距离问题发表的时间）和 Qupdated（距离最后一个回答的时间） 　　改写一下，可以看得更清楚： 　　Qage 和 Qupdated 的单位都是秒。如果一个问题的存在时间越久，或者距离上一次回答的时间越久，Qage 和 Qupdated 的值就相应增大。 　　也就是说，随着时间流逝，这两个值都会越变越大，导致分母增大，因此总得分会越来越小。 ５）总结 　　Stack Overflow 热点问题的排名，与参与度（Qviews 和 Qanswers）和质量（Qscore 和 Ascores）成正比，与时间（Qage 和 Qupdated）成反比。 > 备注(tzg)：分母中的Qupdated是相比上面HN,Reddit的创新点，对好久不更新的回答惩罚 ### 牛顿冷却定律 $$ T=T_{0} e^{-\alpha\left(t-t_{0}\right)} $$ - T(t)是温度T的关于时间t的函数。微积分知识告诉我们，温度变化（冷却）的速率就是温度函数的导数T'(t)。 - $T_{0}$是文章的初始温度，比如100 - $t-t_{0}为距离创建时间的小时数$ - 常数α（α>0）表示冷却系数；如果你想放慢"热文排名"的更新率，"冷却系数"就取一个较小的值，否则就取一个较大的值。  ### 威尔逊区间 $$ \frac{p+\frac{1}{2 n} z_{1-\alpha / 2}^{2} \pm z_{1-\alpha / 2} \sqrt{\frac{p(1-p)}{n}+\frac{z_{1-\alpha / 2}^{2}}{4 n^{2}}}}{1+\frac{1}{n} z_{1-\alpha / 2}^{2}} $$ 置信区间的实质，就是进行可信度的修正，弥补样本量过小的影响。如果样本多，就说明比较可信，不需要很大的修正，所以置信区间会比较窄，下限值会比较大；如果样本少，就说明不一定可信，必须进行较大的修正，所以置信区间会比较宽，下限值会比较小。威尔逊区间很好地解决了小样本的准确性问题。 - $p表示样本的"赞成票比例"$ - n表示样本的大小 - $z_{1-\alpha / 2}$表示对应某个置信水平的z统计量，这是一个常数，可以通过查表或统计软件包得到。一般情况下，在95%的置信水平下，z统计量的值为1.96。 结论：可以看到，当n的值足够大时，这个下限值会趋向p。如果n非常小（投票人很少），这个下限值会大大小于p。实际上，起到了降低"赞成票比例"的作用，使得该项目的得分变小、排名下降。 > 备注(tzg) 威尔逊区间的优势就是它的缺点，导致总体偏向头部，而尾部的新内容因为样本量较少所以很难排上去 ### IMDB算法（贝叶斯算法,电影评分） $$ WR = \frac{v}{v+m} * R + \frac{m}{v+m} * C $$ - WR， 加权得分（weighted rating） - R， 该电影的用户投票的平均得分（Rating） - v， 该电影的投票人数（votes） - m， 排名前 250 名的电影的最低投票数 - C， 所有电影的平均得分 ### 梅西法（BCS体育赛事） $$ X^T Xr=X^T y $$ - $X^TX构造为如下矩阵，对角元素就是队伍i完成的比赛场数;i,j每有一个比赛/评价，非对角元素ij和ji位置的值减一。$ - $针对X^Ty的第i个元素就是队伍i所有比赛获得的分差之和。$ 这里简单分析下$X^TX$是一个n阶对称方阵，也是一个对角阵，并且每一列线性相关。 为了让r有唯一解，往往需要给$X^TX$和$X^Ty$增加一行0，表示每个队伍所有评分总和为0. 总结：梅西法看中的是评分的分差，利用它给出不同项目的打分，进而排名。 ### 科利法（Netflix电影评分） $$ Cr=b $$ -