C++解释器模式 C++设计模式之解释器模式
果冻想 人气:0前言
那日,闲的无聊,上了一个在线编程学习网站;最近那个在线编程学习网站很火啊;之前,盖茨、扎克伯格等大人物都来宣传了,思想是人人都应该学习编程;我一想就这算怎么回事啊?这要是在中国,还让人活不?话题不扯开了,还是说我上了那个在线编程网站吧,首先是给你玩一个小游戏,激发你对编程的兴趣。游戏是这样的,网页上有一个编辑框,屏幕上有一只小狗,比如你在编辑框中输入这样的句子:down run 10;按下回车,这个时候,你就看到屏幕上的小狗向下跑动了10个方格大小的长度;你再输入up walk 5,按下回车,小狗就会向上走动5个方格大小的长度。确实是有点意思;但是,对于我这种已经不需要这种游戏来激起我学习兴趣的人来说,我更喜欢的是去考虑它是如何实现的,如何将我输入的一句话去控制小狗移动的。而这一切的一切都不得不说到今天总结的解释器模式了。
解释器模式
在GOF的《设计模式:可复用面向对象软件的基础》一书中对解释器模式是这样说的:给定一个语言,定义它的文法的一种表示,并定义一个解释器,这个解释器使用该表示来解释语言中的句子。如果一种特定类型的问题发生的频率足够高,那么可能就值得将该问题的各个实例表述为一个简单语言中的句子。这样就可以构建一个解释器,该解释器通过解释这些句子来解决该问题。
就如上面说的那个游戏,我输入up walk 5,我必须按照:移动方向+移动方式+移动距离这种格式输入我的指令,而这种格式的指令就是一种文法,只有按照了我定义的这种文法去输入,才能控制屏幕上的小狗去移动。当然了,我输入up walk 5,屏幕上的小狗肯定是听不懂的,它不知道我输入的是什么,这个时候需要怎么办?我需要一个工具去将我输入的内容翻译成小狗能听懂的东西,而这个工具就是定义中提到的解释器,解释器对我输入的指令进行解释,然后将解释得到的指令发送给屏幕上的小狗,小狗听懂了,就进行实际的移动。
我们在开发中经常用到的正则表达式也是这类问题的代表。我们有的时候需要去匹配电话号码、SFZ号;我们不用为了每一种匹配都写一个特定的算法,我们可以为每一种匹配定义一种文法,然后去解释这种文法定义的句子就ok了。
文法规则和抽象语法树
上面对于解释器模式的定义中,提及到了一个词:文法。在使用代码实现解释器模式之前,是非常有必要去学习一下文法的概念,以及如何表示一个语言的文法规则。再拿上面的游戏这个例子进行说明,我可以定义以下五条文法:
expression ::= direction action distance | composite //表达式
composite ::= expression 'and' expression //复合表达式
direction ::= 'up' | 'down' | 'left' | 'right' //移动方向
action ::= 'move' | 'walk' //移动方式
distance ::= an integer //移动距离
上面的5条文法规则,对应5个语言单位,这些语言单位可以分为两大类:一类为终结符(也叫做终结符表达式),例如上面的direction、action和distance,它们是语言的最小组成单位,不能再进行拆分;另一类为非终结符(也叫做非终结符表达式),例如上面的expression和composite,它们都是一个完整的句子,包含一系列终结符或非终结符。
我们就是根据上面定义的一些文法可以构成更多复杂的语句,计算机程序将根据这些语句进行某种操作;而我们这里列出的文法,计算机是无法直接看懂的,所以,我们需要对我们定义的文法进行解释;就好比,我们编写的C++代码,计算机是看不懂的,我们需要进行编译一样。解释器模式,就提供一种模式去给计算机解释我们定义的文法,让计算机根据我们的文法去进行工作。
在文法规则定义中可以使用一些符号来表示不同的含义,如使用“|”表示或,使用“{”和“}”表示组合,使用“*”表示出现0次或多次等,其中使用频率最高的符号是表示“或”关系的“|”,如文法规则“bool Value ::= 0 | 1”表示终结符表达式bool Value的取值可以为0或者1。
除了使用文法规则来定义一个语言,在解释器模式中还可以通过一种称之为抽象语法树的图形方式来直观地表示语言的构成,每一棵语法树对应一个语言实例,对于上面的游戏文法规则,可以通过以下的抽象语法树来进行表示:
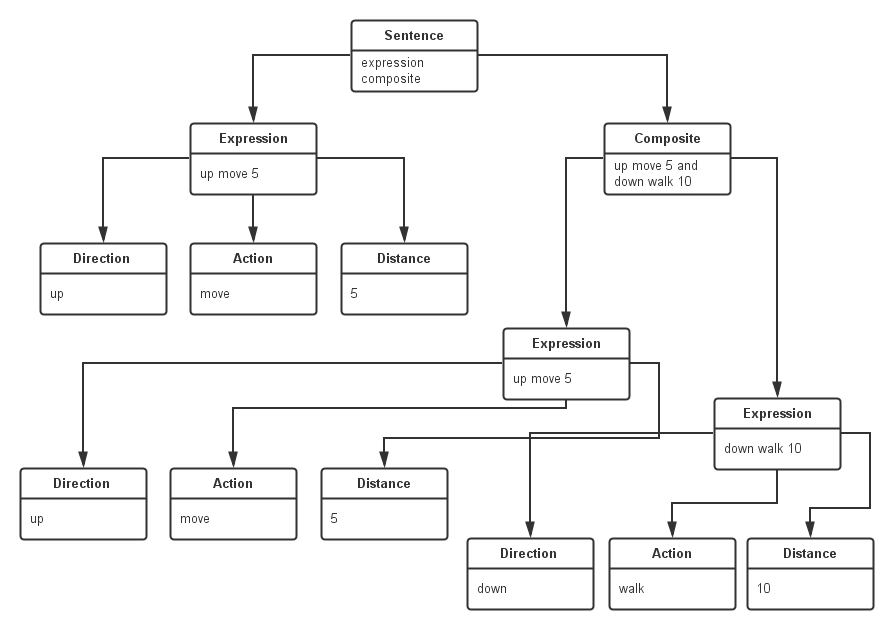
在抽象语法树种,可以通过终结符表达式和非终结符表达式组成复杂的语句,每个文法规则的语言实例都可以表示为一个抽象语法树,就是说每一条具体的语句都可以用类似上图所示的抽象语法树来表示,在图中终结符表达式类的实例作为树的叶子节点,而非终结符表达式类的实例作为非叶子节点。抽象语法树描述了如何构成一个复杂的句子。
UML类图
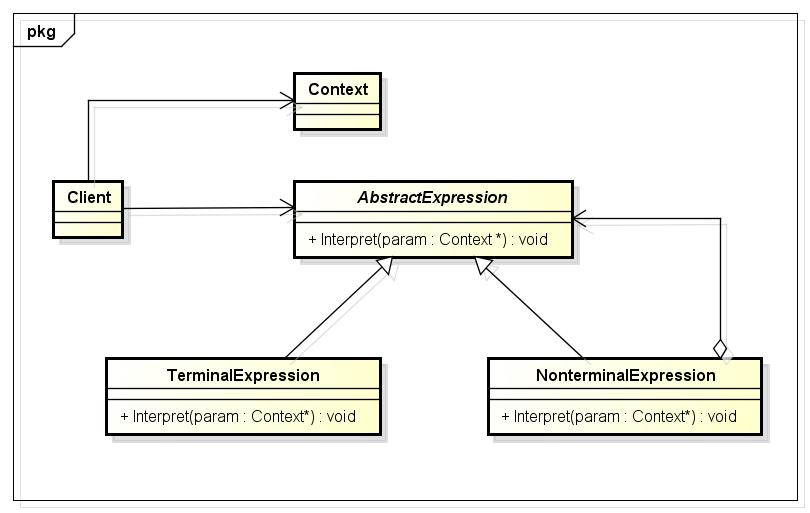
AbstractExpression:声明一个抽象的解释操作,这个接口被抽象语法树中所有的节点所共享;
TernimalExpression:一个句子中的每个终结符需要该类的一个实例,它实现与文法中的终结符相关联的解释操作;
NonternimalExpression:
1.对于文法中的每一条规则都需要一个NonternimalExpression类;
2.为文法中的的每个符号都维护一个AbstractExpression类型的实例变量;
3.为文法中的非终结符实现解释操作,在实现时,一般要递归地调用表示文法符号的那些对象的解释操作;
Context:包含解释器之外的一些全局信息;
Client:构建一个需要进行解释操作的文法句子,然后调用解释操作进行解释。
实际进行解释时,按照以下时序进行的:
1.Client构建一个句子,它是NonterminalExpression和TerminalExpression的实例的一个抽象语法树,然后初始化上下文并调用解释操作;
2.每一非终结符表达式节点定义相应子表达式的解释操作。而各终结符表达式的解释操作构成了递归的基础;
3.每一节点的解释操作用作用上下文来存储和访问解释器的状态。
使用场合
在以下情况下可以考虑使用解释器模式:
1.可以将一个需要解释执行的语言中的句子表示为一个抽象语法树;
2.一些重复出现的问题可以用一种简单的语言来进行表达;
3.一个语言的文法较为简单;
4.执行效率不是关键问题。【注:高效的解释器通常不是通过直接解释抽象语法树来实现的,而是需要将它们转换成其他形式,使用解释器模式的执行效率并不高。】
代码实现
我们这里用代码来实现上面的游戏,只不过不是控制小狗在屏幕上移动了,而是将对应的控制指令翻译成汉语进行表示,这和翻译成控制小狗移动的指令的原理是一样的。比如现在有指令:down run 10;那么,经过解释器模式得到的结果为:向下跑动10。
#include <iostream>
#include <vector>
using namespace std;
#define MAX_SIZE 256
#define SAFE_DELETE(p) if (p) { delete p; p = NULL; }
const wchar_t *const DOWN = L"down";
const wchar_t *const UP = L"up";
const wchar_t *const LEFT = L"left";
const wchar_t *const RIGHT = L"right";
const wchar_t *const MOVE = L"move";
const wchar_t *const WALK = L"walk";
class AbstractNode
{
public:
virtual wchar_t *Interpret() = 0;
};
class AndNode : public AbstractNode
{
public:
AndNode(AbstractNode *left, AbstractNode *right) : m_pLeft(left), m_pRight(right){}
wchar_t *Interpret()
{
wchar_t *pResult = new wchar_t[MAX_SIZE];
memset(pResult, 0, MAX_SIZE * sizeof(wchar_t));
wchar_t *pLeft = m_pLeft->Interpret();
wchar_t *pRight = m_pRight->Interpret();
wcscat_s(pResult, MAX_SIZE, pLeft);
wcscat_s(pResult, MAX_SIZE, pRight);
SAFE_DELETE(pLeft);
SAFE_DELETE(m_pRight);
return pResult;
}
private:
AbstractNode *m_pLeft;
AbstractNode *m_pRight;
};
class SentenceNode : public AbstractNode
{
public:
SentenceNode(AbstractNode *direction, AbstractNode *action, AbstractNode *distance) :
m_pDirection(direction), m_pAction(action), m_pDistance(distance){}
wchar_t *Interpret()
{
wchar_t *pResult = new wchar_t[MAX_SIZE];
memset(pResult, 0, MAX_SIZE * sizeof(wchar_t));
wchar_t *pDirection = m_pDirection->Interpret();
wchar_t *pAction = m_pAction->Interpret();
wchar_t *pDistance = m_pDistance->Interpret();
wcscat_s(pResult, MAX_SIZE, pDirection);
wcscat_s(pResult, MAX_SIZE, pAction);
wcscat_s(pResult, MAX_SIZE, pDistance);
SAFE_DELETE(pDirection);
SAFE_DELETE(pAction);
SAFE_DELETE(pDistance);
return pResult;
}
private:
AbstractNode *m_pDirection;
AbstractNode *m_pAction;
AbstractNode *m_pDistance;
};
class DirectionNode : public AbstractNode
{
public:
DirectionNode(wchar_t *direction) : m_pDirection(direction){}
wchar_t *Interpret()
{
wchar_t *pResult = new wchar_t[MAX_SIZE];
memset(pResult, 0, MAX_SIZE * sizeof(wchar_t));
if (!_wcsicmp(m_pDirection, DOWN))
{
wcscat_s(pResult, MAX_SIZE, L"向下");
}
else if (!_wcsicmp(m_pDirection, UP))
{
wcscat_s(pResult, MAX_SIZE, L"向上");
}
else if (!_wcsicmp(m_pDirection, LEFT))
{
wcscat_s(pResult, MAX_SIZE, L"向左");
}
else if (!_wcsicmp(m_pDirection, RIGHT))
{
wcscat_s(pResult, MAX_SIZE, L"向右");
}
else
{
wcscat_s(pResult, MAX_SIZE, L"无效指令");
}
SAFE_DELETE(m_pDirection);
return pResult;
}
private:
wchar_t *m_pDirection;
};
class ActionNode : public AbstractNode
{
public:
ActionNode(wchar_t *action) : m_pAction(action){}
wchar_t *Interpret()
{
wchar_t *pResult = new wchar_t[MAX_SIZE];
memset(pResult, 0, MAX_SIZE * sizeof(wchar_t));
if (!_wcsicmp(m_pAction, MOVE))
{
wcscat_s(pResult, MAX_SIZE, L"移动");
}
else if (!_wcsicmp(m_pAction, WALK))
{
wcscat_s(pResult, MAX_SIZE, L"走动");
}
else
{
wcscat_s(pResult, MAX_SIZE, L"无效指令");
}
SAFE_DELETE(m_pAction);
return pResult;
}
private:
wchar_t *m_pAction;
};
class DistanceNode : public AbstractNode
{
public:
DistanceNode(wchar_t *distance) : m_pDistance(distance){}
wchar_t *Interpret()
{
wchar_t *pResult = new wchar_t[MAX_SIZE];
memset(pResult, 0, MAX_SIZE * sizeof(wchar_t));
wcscat_s(pResult, MAX_SIZE, m_pDistance);
SAFE_DELETE(m_pDistance);
return pResult;
}
private:
wchar_t *m_pDistance;
};
class InstructionHandler
{
public:
InstructionHandler(wchar_t *instruction) : m_pInstruction(instruction), m_pTree(NULL){}
void Handle();
void Output();
private:
void SplitInstruction(wchar_t **&instruction, int &size);
wchar_t *m_pInstruction;
AbstractNode *m_pTree;
};
void InstructionHandler::Handle()
{
AbstractNode *pLeft = NULL;
AbstractNode *pRight = NULL;
AbstractNode *pDirection = NULL;
AbstractNode *pAction = NULL;
AbstractNode *pDistance = NULL;
vector<AbstractNode *> node; // Store the instruction expression
// Split the instruction by " "
wchar_t **InstructionArray = NULL;
int size;
SplitInstruction(InstructionArray, size);
for (int i = 0; i < size; ++i)
{
if (!_wcsicmp(InstructionArray[i], L"and")) // The instruction is composited by two expressions
{
wchar_t *pDirectionStr = InstructionArray[++i];
pDirection = new DirectionNode(pDirectionStr);
wchar_t *pActionStr = InstructionArray[++i];
pAction = new ActionNode(pActionStr);
wchar_t *pDistanceStr = InstructionArray[++i];
pDistance = new DistanceNode(pDistanceStr);
pRight = new SentenceNode(pDirection, pAction, pDistance);
node.push_back(new AndNode(pLeft, pRight));
}
else
{
wchar_t *pDirectionStr = InstructionArray[i];
pDirection = new DirectionNode(pDirectionStr);
wchar_t *pActionStr = InstructionArray[++i];
pAction = new ActionNode(pActionStr);
wchar_t *pDistanceStr = InstructionArray[++i];
pDistance = new DistanceNode(pDistanceStr);
pLeft = new SentenceNode(pDirection, pAction, pDistance);
node.push_back(pLeft);
}
}
m_pTree = node[node.size() - 1];
}
void InstructionHandler::Output()
{
wchar_t *pResult = m_pTree->Interpret();
setlocale(LC_ALL,"");
wprintf_s(L"%s\n", pResult);
SAFE_DELETE(pResult);
}
void InstructionHandler::SplitInstruction(wchar_t **&instruction, int &size)
{
instruction = new wchar_t*[10];
memset(instruction, 0, 10 * sizeof( wchar_t*));
for (int i = 0; i < 10; ++i)
{
instruction[i] = new wchar_t[10];
memset(instruction[i], 0, 10 * sizeof(wchar_t));
}
size = 0;
int n = 0;
while (*m_pInstruction != L'\0')
{
if (*m_pInstruction == L' ')
{
size++;
m_pInstruction++;
n = 0;
continue;
}
instruction[size][n++] = *m_pInstruction++;
}
size++;
}
int main()
{
wchar_t *pInstructionStr = L"up move 5 and down walk 10";
InstructionHandler *pInstructionHandler = new InstructionHandler(pInstructionStr);
pInstructionHandler->Handle();
pInstructionHandler->Output();
SAFE_DELETE(pInstructionHandler);
}
在上面的代码中,我没有用到Context类,一般Context类作为环境上下文类,用于存储解释器之外的一些全局信息,它通常作为参数被传递到所有表达式的解释方法interpret中,可以在Context对象中存储和访问表达式解释器的状态,向表达式解释器提供一些全局的、公共的数据,此外还可以在Context中增加一些所有表达式解释器都共有的功能,减轻解释器的职责。而我们在代码中定义的一些常量,完全可以放入到Context类中,作为上下文的全局数据。
主要优点
1.易于改变和扩展文法。由于在解释器模式中使用类来表示语言的文法规则,因此可以通过继承等机制来改变或扩展文法;
2.每一条文法规则都可以表示为一个类,因此可以方便地实现一个简单的语言;
3.实现文法较为容易;在抽象语法树中每一个表达式节点类的实现方式都是相似的,这些类的代码编写都不会特别复杂;
4.增加新的解释表达式较为方便。如果用户需要增加新的解释表达式只需要对应增加一个新的终结符表达式类或非终结符表达式类,原有表达式类代码无须修改,符合“开闭原则”。
主要缺点
1.对于复杂文法难以维护;在解释器模式中,每一条规则至少需要定义一个类,因此如果一个语言包含太多文法规则,类的个数将会急剧增加,导致系统难以管理和维护,此时可以考虑使用语法分析程序等方式来取代解释器模式;
2.执行效率低;由于在解释器模式中使用了大量的循环和递归调用,因此在解释较为复杂的句子时其速度很慢,而且代码的调试过程也很麻烦。
总结
解释器模式在实际的系统开发中使用的非常少,因为它会引起效率、性能以及维护方面的问题,并且难度较大,一般在一些大中型的框架型项目中能够找到它的身影。而现在又有很多的开源库提供了对实际需要的支持,所以,我们在实际开发中没有必要再去重复造轮子,能够理解了解释器模式就好了。
加载全部内容