数据结构 2 字符串 数组、二叉树以及二叉树的遍历

上一节的学习中，我们已经结合JAVA 本身，将线性表所包含的顺序表、链表、栈、队列等数据结构通通学习了一番，并且将这些数据结构的一些基本操作。比如 - add() - remove() - pop() 等等方法都进行了列举，通过这些，我们将对线性表有了一个直接的认识。这节将学习有关字符串、广义表等内容。 ## 字符串 怎么理解字符串呢，想必大家都知道。我们在学习JAVA 8大基本类型的时候就有学习到字符串，但是JAVA 里面的字符串是一个`对象` 它是一个引用类型，并且初始化后，是一个`不可变对象` ```java String str = "hello"; ``` 很简单，我们通过一句代码，就可以将一个字符串常量化出来，为什么说常量化呢，这里我们没有采用new 的方式，所以这个变量其实是保存在了常量池里面。而不是堆里面。 从严格意义来说，字符串其实也是符合 `线性结构` 的，因为我们都知道，字符串都是由基本类型的字符 `char` 连接起来组成的，他们存在`一对一`的关系。只不过这个线性表里面存的全部都是字符类型罢了。 ```java private final char value[]; public String() { this.value = "".value; } ``` 通过直接new 的方式，我们可以发现，构造函数里面其实是用一个字符数组来进行储存字符串的，我们这里的数组其实是一个静态数组，它不像List 一样，可以自由的变化长度，初始化了。它就确定死了，多长就多长。 ### 字符串的储存方式 - 普通数组定长储存（String） - 堆分配内存：动态数组储存（StringBuffer） - 链表储存 ```java public StringBuffer(String str) { super(str.length() + 16); append(str); } ------------------ char[] value; AbstractStringBuilder(int capacity) { value = new char[capacity]; } public AbstractStringBuilder append(String str) { if (str == null) return appendNull(); int len = str.length(); ensureCapacityInternal(count + len); str.getChars(0, len, value, count); count += len; return this; } ``` `ensureCapacityInternal` 就是进行扩容的操作。这里的Stringbuffer 就是在堆上面进行的操作。可以像线性表一样。进行扩容操作。 ### BF 算法 BF算法是一种最普通的算法，在指定的字符串中匹配子串，匹配到则返回子串开始的下标。这个算法在String 当中最具有代表性的就是`indexOf(String str)` 这个方法了。 ```java static int indexOf(char[] source, int sourceOffset, int sourceCount, char[] target, int targetOffset, int targetCount, int fromIndex) { if (fromIndex >= sourceCount) { return (targetCount == 0 ? sourceCount : -1); } if (fromIndex < 0) { fromIndex = 0; } if (targetCount == 0) { return fromIndex; } char first = target[targetOffset]; int max = sourceOffset + (sourceCount - targetCount); for (int i = sourceOffset + fromIndex; i <= max; i++) { /* Look for first character. */ if (source[i] != first) { while (++i <= max && source[i] != first); } /* Found first character, now look at the rest of v2 */ if (i <= max) { int j = i + 1; int end = j + targetCount - 1; for (int k = targetOffset + 1; j < end && source[j] == target[k]; j++, k++); if (j == end) { /* Found whole string. */ return i - sourceOffset; } } } return -1; } ``` IndexOf(str) 相比于BF(暴力)还是有很多优化的地方，比如首先会判断首字符是否相同，若首字符都不相同，那直接不用说了。跳过了一些重复的地方。   n 表示子串的长度 m表示源字符串的长度 这个算法最优的时候，若直接在首位碰到，则时间复杂度 `O(n)` 最不幸的要是最后一位才可以碰到，则必须要循环 m*n 次 则时间复杂度 `O(M*N)` ## 数组 数组我在之前就介绍过，一种最基本的存储结构。在线性表的几种分类中。顺序表底层就是使用数组来实现的。 从本质上说，数组作为一种储存结构，而不是一种基本类型，可以理解为容纳基本类型的一个容器。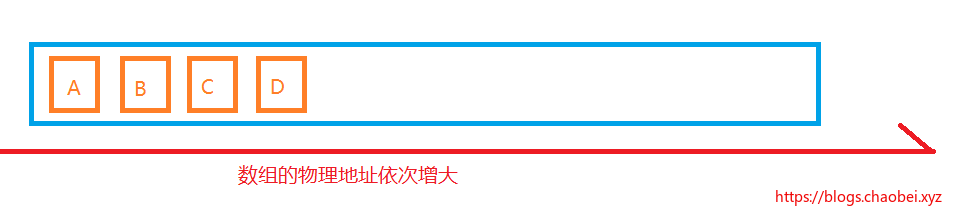 常见的一维数组，其实是很简单的，  指定一个一维数组，指定大小后，它的大小是不可再变的。并且数组元素的类型全部是统一的。 ## 结构树 数据结构的树存储结构中。常用语存储`一对多`的数据，树结构当中，常用的还是二叉树、以及红黑树等，我这里一一介绍。 ### 二叉树 二叉树是结构树里面最有名也是使用最多的树结构数据结构，检查一个树是否满足二叉树，从两个方面下手 1. 每个节点下最多挂两个子节点 只能是0、1、2 2. 树的本身是有序的 如何来确定这个树是否是一个有序树还是无序树呢？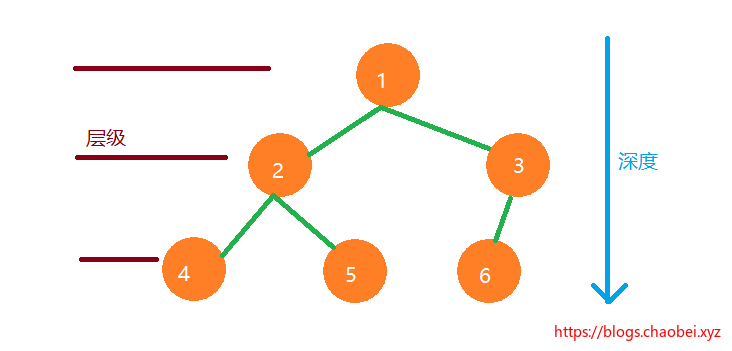 - 按照一定的规则将节点左右分布，那就是有序树，反之则是无序树  ### 二叉树规律 按照前人的总结，我们可以得出以下结论。 - 一个深度为K 的二叉树，最多包含节点数 `2的k次方-1` - 二叉树指定n 层级所包含的节点数为 `2的n-1次方` 如果将二叉树在细分的话，又可以分为满二叉树与完全二叉树。 ### 满二叉树 一听这个名字，就可以理解到。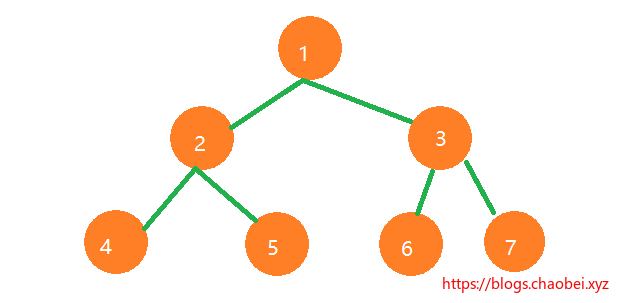它是满（饱和）的，所以，来用画图表示一下  如果二叉树除了叶子节点以外，所有的节点的度都是2（有两个子元素），那么它就是满二叉树 ### 完全二叉树 如果二叉树除去叶子节点是一个满二叉树，并且叶子节点从左向右依次排列。那么这就是一个完全二叉树。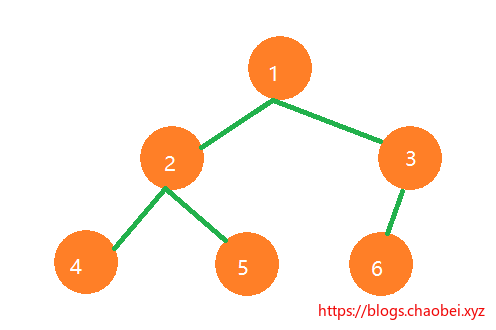  但是，这样排列的却不能成为是完全二叉树。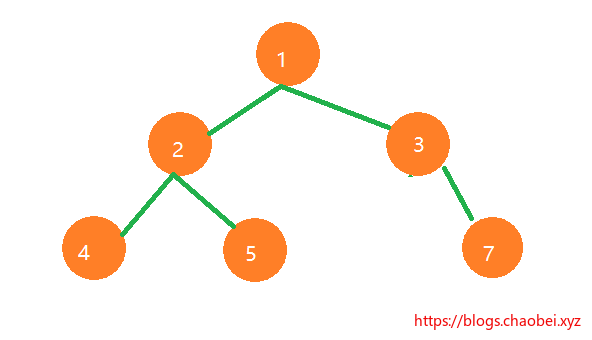  ### 完全二叉树性质 完全二叉树不但具有普通二叉树的性质，并且还有自己的一些独特性质。例如： - 具有n个节点的完全二叉树的深度是 `⌊log2n⌋+1。` ## 二叉树的存储方式 对于满二叉树以及完全二叉树，完全可以采用数组的方式来存储，因为数组就是用来存储对于一对一线性规律的。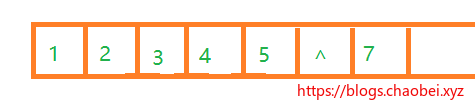所以完全合适   对于没有元素的位置，使用`^` 空处位置。要是遇到刁钻一些的二叉树，例如下面这个，那直接很浪费空间。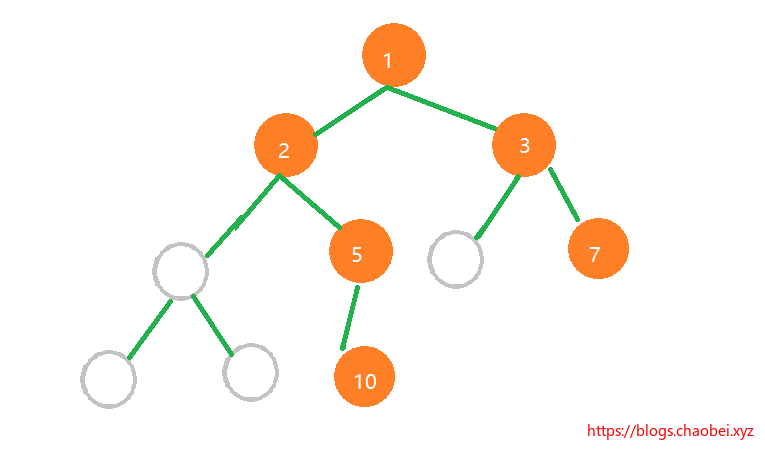  这里面的灰色代表元素缺失，这样存储到数组里面的话，是很浪费内存空间的。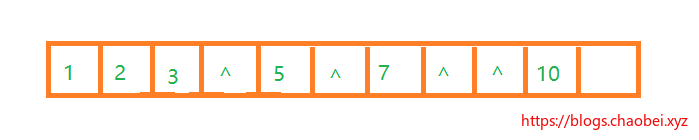  ## 链式二叉树 当然，我们既然不能用数组存储，那就使用指针存储。我们知道二叉树的定义里已经规定好，儿子节点不能超过两个，并且本身还需要是一个有序树  每一个节点需要包含两个指针，用于指向左节点和右节点即可。中间则包含本节点的数据即可。这样相比于数组，我们之前也学习过链表、虽然数据不再是连续的，但是可以随意的增加节点、不会造成内存空间的浪费。 ## 二叉树遍历 一个二叉树的遍历，是为了访问其所有的节点。有这样几种方式 - 前序遍历 - 中序遍历 - 后序遍历 - 层序遍历 ### 前序遍历 通俗的说就是从二叉树的根节点出发，先访问当前节点的左节点，一直向下。直到当前节点没有左节点，再遍历右节点。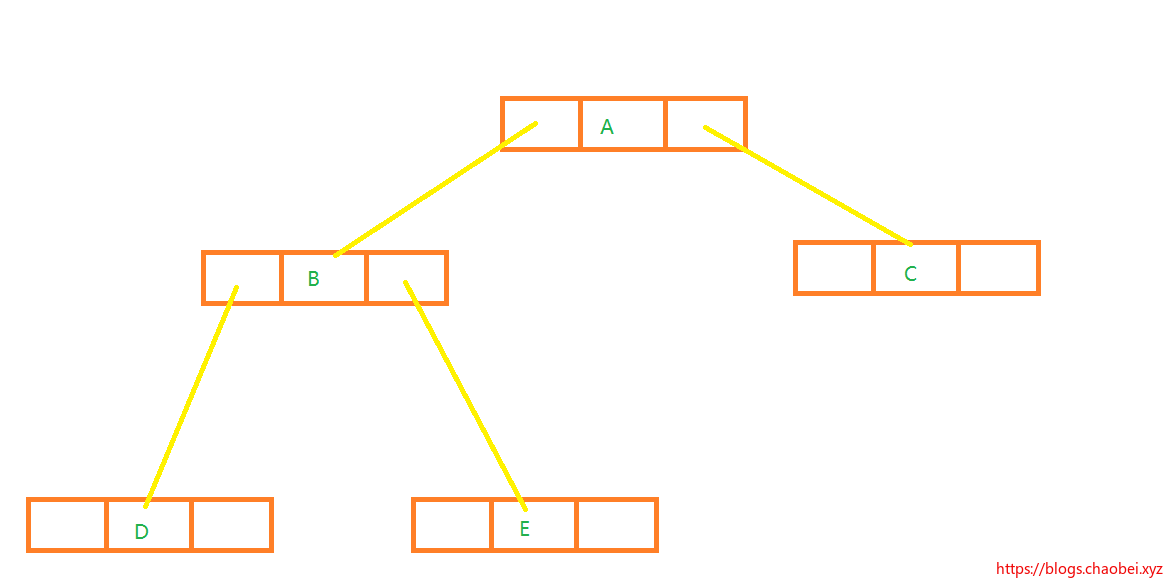  我们按照当前图所示，简单讲解一下： 1. 从A根节点入手，打印A 2. 访问A节点的左节点 打印B 3. 访问当前节点的左节点，打印D 4. D没有左右节点，本次遍历完成，访问B节点右分支 打印E 5. E节点没有左右分支，遍历本节点结束。 6. 遍历A节点右分支，打印C 7. C没有左右节点，A节点遍历完成。退出循环。 以上的打印顺序应该是：`ABDEC` ### 中序遍历 中序遍历，最大的特点就是：第二次到达节点输出内容，也是从左到右的顺序，从根节点出发。 还是按照上面那张图： 1. 从A出发，找到B 2. 在B找到D 3. D节点没有左右节点，打印D 4. 第二次回到B 打印B 5. 访问B节点右节点E 6. E没有左右节点，第二次回到E 打印E 7. B完成，回到A,打印A 8. 访问A右节点C,没有左右节点直接打印C 经过以上打印访问，顺序为：`DBEAC` ### 后序遍历 后序遍历，在原有中序遍历上稍微有些不同，当第`三次到达`节点时，才会输出，还是按照根节点入手，从左到右的方式。 1. A节点入手，到达B 2. B节点左节点，到达D 3. D节点没有左右节点，直接打印D 4. 回到B节点，第二次到达，到E节点 5. E节点没有左右节点，直接打印E 6. 回到B,第三次到达，打印B 7. 回到A 第二次到达，到达C 8. 直接打印C,回到A 第三次到达，打印A 最后的顺序应该是：`DEBCA` ### 层序遍历 之前已经说过了有关层次的相关概念。层序遍历，主要思路是：通过借助队列，从树的根节点开始，左右节点节点入队，每次队列中一个节点出队，直到所有的节点都出队。出队的先后顺序就是遍历的结果。  按照这幅图来说明一下： 1. 首先根节点1入队。 2. 根节点1出队，同时将1的两个子节点`2,3`放入队列 3. 队列头2出队，将2节点的两个子节点`4,5`放入队列 4. 队列头3出队，同时将3的两个子节点`6,7`放入队列 5. 不断循环，直到队列为空。则遍历完成。 ## 小结 通过本节，应该了解到树这个重要的概念。以及树当中最常见的二叉树的遍历以及使用。并且了解字符串、数组等基本概念 ## 参考 http://c.biancheng.net/view/3392.html https://www.jianshu.com/p/a47d6ed886c8