[Statistics] Comparison of Three Correlation Coefficient: Pearson, Kendall, Spearman

时间:2020-03-04 Sherrrry 人气:1

There are three popular metrics to measure the correlation between two random variables: Pearson's correlation coefficient, Kendall's tau and Spearman's rank correlation coefficient. In this article, I will make a detailed comparison among the three measures and discuss how to choose among them.

Definition

Pearson Correlation

Pearson's correlation coefficient is the covariance of the two variables divided by the product of their standard deviations.

The formula for {\displaystyle \rho } can be expressed in terms of mean and expectation. Since

the formula for {\displaystyle \rho } can also be written as

Kendall's Tau

Let (x₁, y₁), (x₂, y₂), ..., (x_n, y_n) be a set of observations of the joint random variables X and Y respectively, such that all the values of ({\displaystyle x_{i}}) and ({\displaystyle y_{i}}) are unique. Any pair of observations {\displaystyle (x_{i},y_{i})} and {\displaystyle (x_{j},y_{j})}, where {\displaystyle i<j}, are said to be concordant if the ranks for both elements (more precisely, the sort order by x and by y) agree: that is, if both {\displaystyle x_{i}>x_{j}} and {\displaystyle y_{i}>y_{j}}; or if both {\displaystyle x_{i}<x_{j}} and {\displaystyle y_{i}<y_{j}}. They are said to be discordant, if {\displaystyle x_{i}>x_{j}} and {\displaystyle y_{i}<y_{j}}; or if {\displaystyle x_{i}<x_{j}} and {\displaystyle y_{i}>y_{j}}. If {\displaystyle x_{i}=x_{j}} or {\displaystyle y_{i}=y_{j}}, the pair is neither concordant nor discordant.

The Kendall τ coefficient is defined as:

Consequently,

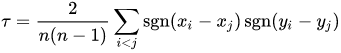
Spearman's Rank Correlation Coefficient

The Spearman correlation coefficient is defined as the Pearson correlation coefficient between the rank variables.

For a sample of size n, the n raw scores {\displaystyle X_{i},Y_{i}} are converted to ranks {\displaystyle \operatorname {rg} X_{i},\operatorname {rg} Y_{i}}, and {\displaystyle r_{s}} is computed as

To compute Spearman’s correlation, we have to compute the rank of each value, which is its index in the sorted sample. Then we compute Pearson’s correlation for the ranks.

加载全部内容