实现一个简单的解释器(5)
Xlgd 人气:2译自:https://ruslanspivak.com/lsbasi-part5/
(已获得作者授权)
你如何处理和了解像创建解释器或编译器这样复杂的事情?在开始时,一切看上去都像是一团乱七八糟的纱线,你需要解开缠结才能得到完美的球。
到达那里的方法是将它解开一个线,一次解开一个结。不过有时候,你可能会觉得自己听不懂某些内容,但必须继续前进,我向你保证,如果你足够坚持,它最终将“咔嗒”一声被解开。
在理解如何创建解释器和编译器的过程中,最好的建议之一是阅读文章中的解释,阅读代码,然后自己编写代码,甚至在一段时间里编写相同的代码,使你能完全了解材料和代码,然后继续学习新主题。不要着急,只要放慢脚步,花点时间深刻理解基本概念,这种方法虽然看似很慢,但会在未来获得回报。相信我。
最后,最终将获得完美的毛线球,即使不是那么完美,它也比什么也不做或者快速浏览后的几天内忘掉好多了。
请记住:一步步理解这些知识点,并通过编写代码练习所学的知识:
今天,你将使用前几篇文章中获得的知识,学习如何解析和解释具有任意数量的加,减,乘和除运算的算术表达式,你将编写一个解释器,该解释器将能够对"14 + 2 * 3 - 6 / 2"之类的表达式求值。
在深入学习并编写一些代码之前,我们先讨论一下运算符的结合性(associativity)和优先级(associativity)。
按照惯例7 + 3 + 1与(7 + 3)+ 1相同,而7 - 3 - 1相当于(7 - 3)- 1。 我们都了解这些。如果我们将7 - 3 - 1视为7 -(3 - 1),则结果将会意外的变成5,而不是我们预期的3。
在普通算术和大多数编程语言中,加,减,乘和除是左结合(left-associative)的:
7 + 3 + 1 is equivalent to (7 + 3) + 1
7 - 3 - 1 is equivalent to (7 - 3) - 1
8 * 4 * 2 is equivalent to (8 * 4) * 2
8 / 4 / 2 is equivalent to (8 / 4) / 2什么是运算符号的左结合性呢?
当表达式7 + 3 + 1中的3之类的操作数在两侧都带有加号时,我们需要约定来确定哪个运算符适用于3,是左边的加号还是右边的加号?我们说运算符加号左结合,是因为在存在两侧都带有加号的操作数时,此时左边的加号适用于此操作数,因此我们说运算符加号是左结合的(The operator + associates to the left because an operand that has plus signs on both sides belongs to the operator to its left and so we say that the operator + is left-associative.),所以按照结合性惯例,7 + 3 + 1等于(7 + 3)+ 1。
我们再来看7 + 5 * 2这个表达式,在操作数5的两边都有不同类型的运算符,该表达式等于7 +(5 * 2)还是(7 + 5)* 2呢?我们如何解决这种歧义?
在这种情况下,结合性约定对我们没有帮助,因为它仅适用于加减法(+,-)或乘除法(*,/)这种同一类型的运算符。当我们在同一表达式中具有不同种类的运算符时,我们需要另一种约定来解决歧义。我们需要一个定义运算符相对优先级的约定。
我们说如果运算符乘号在加号之前执行其操作数,则乘号具有更高的优先级(higher precedence)。在我们所使用的运算中,乘法和除法的优先级高于加法和减法,所以表达式7 + 5 * 2等效于7 +(5 * 2),表达式7 - 8 / 4等效于7-(8 / 4)。
在含有优先级相同的运算符的表达式中,我们仅使用结合性约定并从左到右执行运算符:
7 + 3 - 1 is equivalent to (7 + 3) - 1
8 / 4 * 2 is equivalent to (8 / 4) * 2希望你不要因为这些运算符的结合性和优先级而感到无聊,我们可以利用这些约定来构造算术表达式的语法,以显示算术运算符的结合性和优先级,然后,我们可以按照我在第4部分中概述的准则将语法转换为代码,我们的解释器将能够处理运算符的优先级和结合性约定。
这是我们的优先级表(precedence table):

从表中可以看出,运算符加号和减号具有相同的优先级,并且它们都是左结合的,还可以看到,运算符乘号和除号也是左结合的,它们之间也具有相同的优先级,但是比加减运算符具有更高的优先级。
以下是有关如何根据优先级表构造语法的规则:
1、为每一类优先级定义一个非终结符。非终极符的产生式主体应包含该类优先级的算术运算符和下一类更高优先级的非终结符。( The body of a production for the non-terminal should contain arithmetic operators from that level and non-terminals for the next higher level of precedence.)
2、为基本的表达单位(在本文下为整数)创建一个附加的非终结符factor。一般规则是,如果具有N类优先级,则总共将需要N + 1个非终结符:每类级别一个非终结符(N个)再加上一个运算基本单位的非终结符factor(1个)。(Create an additional non-terminal factor for basic units of expression, in our case, integers. The general rule is that if you have N levels of precedence, you will need N + 1 non-terminals in total: one non-terminal for each level plus one non-terminal for basic units of expression.)
继续!
让我们遵循规则并构建语法。
根据规则1,我们将定义两个非终结符:一个用于级别2的称为expr的非终结符和一个用于级别1的称为term的非终结符,通过规则2,我们将为算术的基本单位定义一个非终结符factor来表达整数。
新语法的起始符号将为expr,expr的产生式将包含一个表示使用级别2的运算符主体,在本例中为加号和减号,并将包含更高级别优先级的非终结符term。
级别2:

term产生式将包含一个使用级别1运算符的主题,即运算符乘号和除号,并且它也包含基本表达式单位(整数)的非终结符factor:
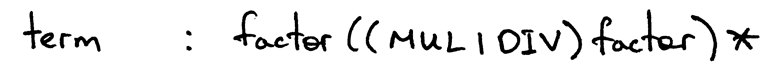
非终结符factor的产生式为:

你已经在之前的文章看见过以上产生式的语法和语法图,在这里,考虑到结合性和优先级,我们将它们组合成一个语法:

这是与上面的语法相对应的语法图:

图中的每个矩形框都是对另一个图的“函数调用(method call)”。 如果你采用表达式7 + 5 * 2并从顶部expr开始,然后一直走到最底部的factor,那么应该能够看到较高优先级的运算符乘号和除号在较低的图中,运算符加号和减号在较高的图中,并且高优先级的运算符先执行。
让我们看一下根据上面的语法和语法图来对算术表达式7 + 5 * 2计算的分解步骤,这是显示高优先级运算符先于低优先级运算符执行的另一种方式:

好的,让我们按照第4部分中的指导方法将语法转换为代码,然后看看我们的新解释器如何工作。
这是语法:

这是计算器的完整代码,可以处理包含任意数量的加,减,乘和除整数运算的有效算术表达式。
与第4部分中的代码相比,以下是主要改变的地方:
1、Lexer类现在可以对+,-,*和/进行标记化(这里没有什么新鲜的,我们只是将以前文章中的代码组合到一个支持所有这些Token的类中)
2、回想一下,在语法中定义的每个规则(产生式)R都会转换为具有相同名称的函数,并且对该规则的引用会成为函数调用:R(), 所以Interpreter类现在具有对应于语法中三种非终结符函数:expr,term和factor。
源代码:
# Token types
#
# EOF (end-of-file) token is used to indicate that
# there is no more input left for lexical analysis
INTEGER, PLUS, MINUS, MUL, DIV, EOF = (
'INTEGER', 'PLUS', 'MINUS', 'MUL', 'DIV', 'EOF'
)
class Token(object):
def __init__(self, type, value):
# token type: INTEGER, PLUS, MINUS, MUL, DIV, or EOF
self.type = type
# token value: non-negative integer value, '+', '-', '*', '/', or None
self.value = value
def __str__(self):
"""String representation of the class instance.
Examples:
Token(INTEGER, 3)
Token(PLUS, '+')
Token(MUL, '*')
"""
return 'Token({type}, {value})'.format(
type=self.type,
value=repr(self.value)
)
def __repr__(self):
return self.__str__()
class Lexer(object):
def __init__(self, text):
# client string input, e.g. "3 * 5", "12 / 3 * 4", etc
self.text = text
# self.pos is an index into self.text
self.pos = 0
self.current_char = self.text[self.pos]
def error(self):
raise Exception('Invalid character')
def advance(self):
"""Advance the `pos` pointer and set the `current_char` variable."""
self.pos += 1
if self.pos > len(self.text) - 1:
self.current_char = None # Indicates end of input
else:
self.current_char = self.text[self.pos]
def skip_whitespace(self):
while self.current_char is not None and self.current_char.isspace():
self.advance()
def integer(self):
"""Return a (multidigit) integer consumed from the input."""
result = ''
while self.current_char is not None and self.current_char.isdigit():
result += self.current_char
self.advance()
return int(result)
def get_next_token(self):
"""Lexical analyzer (also known as scanner or tokenizer)
This method is responsible for breaking a sentence
apart into tokens. One token at a time.
"""
while self.current_char is not None:
if self.current_char.isspace():
self.skip_whitespace()
continue
if self.current_char.isdigit():
return Token(INTEGER, self.integer())
if self.current_char == '+':
self.advance()
return Token(PLUS, '+')
if self.current_char == '-':
self.advance()
return Token(MINUS, '-')
if self.current_char == '*':
self.advance()
return Token(MUL, '*')
if self.current_char == '/':
self.advance()
return Token(DIV, '/')
self.error()
return Token(EOF, None)
class Interpreter(object):
def __init__(self, lexer):
self.lexer = lexer
# set current token to the first token taken from the input
self.current_token = self.lexer.get_next_token()
def error(self):
raise Exception('Invalid syntax')
def eat(self, token_type):
# compare the current token type with the passed token
# type and if they match then "eat" the current token
# and assign the next token to the self.current_token,
# otherwise raise an exception.
if self.current_token.type == token_type:
self.current_token = self.lexer.get_next_token()
else:
self.error()
def factor(self):
"""factor : INTEGER"""
token = self.current_token
self.eat(INTEGER)
return token.value
def term(self):
"""term : factor ((MUL | DIV) factor)*"""
result = self.factor()
while self.current_token.type in (MUL, DIV):
token = self.current_token
if token.type == MUL:
self.eat(MUL)
result = result * self.factor()
elif token.type == DIV:
self.eat(DIV)
result = result / self.factor()
return result
def expr(self):
"""Arithmetic expression parser / interpreter.
calc> 14 + 2 * 3 - 6 / 2
17
expr : term ((PLUS | MINUS) term)*
term : factor ((MUL | DIV) factor)*
factor : INTEGER
"""
result = self.term()
while self.current_token.type in (PLUS, MINUS):
token = self.current_token
if token.type == PLUS:
self.eat(PLUS)
result = result + self.term()
elif token.type == MINUS:
self.eat(MINUS)
result = result - self.term()
return result
def main():
while True:
try:
# To run under Python3 replace 'raw_input' call
# with 'input'
text = raw_input('calc> ')
except EOFError:
break
if not text:
continue
lexer = Lexer(text)
interpreter = Interpreter(lexer)
result = interpreter.expr()
print(result)
if __name__ == '__main__':
main()将以上代码保存到calc5.py文件中,或直接从GitHub下载,尝试一下,然后自己看看解释器是否正确地计算了具有不同优先级运算符的算术表达式。
这是我的笔记本电脑上的运行效果:
$ python calc5.py
calc> 3
3
calc> 2 + 7 * 4
30
calc> 7 - 8 / 4
5
calc> 14 + 2 * 3 - 6 / 2
17接下来是今天的练习:

1、在不浏览本文代码的情况下编写本文所述的解释器,完成后编写一些测试,并确保它们通过。
2、扩展解释器以处理包含括号的算术表达式,以便你的解释器可以计算深度嵌套的算术表达式,例如:7 + 3 *(10 /(12 /(3 + 1)-1))
最后再来复习回忆一下:
1、运算符的左结合是什么意思?
2、运算符加号和减号是左结合还是右结合? 乘号和除号呢?
3、运算符加号的优先级是否比运算符乘号高?
嘿,你一直阅读到最后! 真的很棒 下次我会再写一篇新文章,敬请期待。
加载全部内容