论文地址：基于通用传递函数GSC和后置滤波的语音增强

博客作者：凌逆战

博客地址：https://www.cnblogs.com/LXP-Never/p/12232341.html

摘要

　　在语音增强应用中，麦克风阵列后置滤波可进一步减少波束形成器输出处的噪声成分。在麦克风阵列结构中，最近提出的通用传递函数广义旁瓣消除器（TF-GSC）在定向噪声场中显示出令人印象深刻的降噪能力，同时仍保持低语音失真。但是，在扩散噪声场中，可获得的降噪效果不明显。当噪声信号不稳定时，性能甚至会进一步下降。 在本文中，我们提出了三种后置滤波方法，以改善麦克风阵列的性能。 其中两个基于单通道语音增强器，并利用了最近提出的与波束形成器输出串联的算法。 第三个是多通道语音增强器，它利用TF-GSC结构中构建的纯噪声组件。 这项工作集主要对后置滤波结构的评估。 做了大量实验研究包括对各种噪声场的客观评估和主观评估，证明了与单通道技术相比，多通道后置滤波的优势。

关键词：广义旁瓣对消器（GSC），麦克风阵列，非平稳性，后置滤波，语音增强

1  引言

　　最近，Gannot等人提出了对Griffiths和Jim[1]经典广义旁瓣对消除器（GSC）的扩展，它处理任意Transfer Functions(传递函数，TFs)^[2]-[3]。这个算法叫做TF-GSC，TF-GSC虽然在定向噪声情况下得到了良好的结果，但在非定向噪声环境（如扩散噪声情况^[4][5]）中，阵列的性能有显著的下降。此外，由于TF-GSC算法利用了语音的非平稳性和噪声的平稳性，因此在非平稳噪声环境下，性能会显著下降。

　　因此，在非定向和非平稳噪声环境中，使用后置滤波来提高波束形成性能。Zelinski^[6]提出了基于Wiener滤波器的简单延迟和和波束形成器的后置滤波方法。后来，后置滤波被合并到Griffiths和Jim-GSC波束形成器中^[7]-[8]。其作者建议连续使用两个后置滤波器。第一个工作在固定波束形成器分支，第二个使用GSC输出。在定向噪声源和扩散噪声场的低频段，各传感器的噪声分量之间存在相关性。虽然在这种情况下第一个后置滤波器变得无用，但后者抑制了噪声。通过使用几个谐波嵌套的子阵列结合Wiener后置滤波器，可以稍微减轻扩散噪声场中的低频段相关性^[9]。 Marro等人^[10]对该结构进行了彻底的分析。

　　注意，波束形成器的输出可能被视为包含语音信号并被（残留）噪声信号污染的单个通道。本研究建议使用最先进的单麦克风语音增强算法。在[11]中，建议使用谱减法算法[12]。

　　本文主要贡献，提出并评估了另外两种现代算法的使用。第一个是mix -maximum (MIXMAX)算法^[13]-[14]。第二种是最优修正的对数谱 振幅估计器(OM-LSA)[15]。然而，如果噪声信号是扩散和非平稳的，单麦克风后置滤波器不能完全抑制它。

　　Cohen和Berdugo [16]首先提出了一种处理非平稳噪声源的方法。 这种后置滤波方法与经典的Griffiths和Jim GSC波束形成器结合使用，并且利用了波束形成器的输出和由阻塞分支产生的噪声参考信号，从而构成了多麦克风后置滤波。

　　本文对该方法进行了扩展，并将其应用于Gannot等人提出的TF-GSC波束形成器中^[2]。TF-GSC的优势在于 即使在高度回响的环境中，它也能够将自身引导至所需的语音信号，并消除了所需的信号泄漏到噪声参考分支中。 新的多麦克风后置滤波器方法在各种噪声场中进行了评估，并与单个麦克风后置滤波器进行了比较。

　　第二节介绍了问题的情况。第三节简要回顾TF-GSC。第四节介绍了所提出的多麦克风后置滤波器。第五节对所提出的方法进行了评估，并与单麦克风后置滤波器进行了比较。第六节得出了一些结论。

2  问题表述

　　在嘈杂和混响环境中，传感器阵列接收到的信号由三部分组成。

1. 语音信号（最初建议使用TF-GSC来增强任意非平稳信号。在此贡献中，我们将讨论仅限于语音信号，因为后置滤波依赖于特定的语音特性）
2. 平稳干扰信号
3. 非平稳(暂态)噪声分量

我们的目标是根据接收到的信号重建语音组件。因此，接收到的信号由

$$公式1：z_{m}(t)=a_{m}(t) * s(t)+n_{m}^{s}(t)+n_{m}^{t}(t) ; \quad m=1, \ldots, M$$

其中$z_m(t)$是第$m$个传感器信号，$s(t)$是所需的语音源，表示卷积运算。$n_m^s(t)$和$n_m^t(t)$分别是稳态和瞬时噪声分量。注意，这两个噪声分量由相干（定向）噪声分量和扩散噪声分量组成。$a_m(t)$是从语音源到第$m$个传感器的第$m$个时变声学传递函数（ATF）。利用短期频率分析和假设时不变ATFs，我们在时频域中具有一个向量形式

$$公式2：Z\left(t, e^{j \omega}\right)=A\left(e^{j \omega}\right) S\left(t, e^{j \omega}\right)+N_{s}\left(t, e^{j \omega}\right)+N_{t}\left(t, e^{j \omega}\right)$$

其中

$$\begin{aligned} Z^{T}\left(t, e^{j \omega}\right)=\left[Z_{1}\left(t, e^{j \omega}\right)\right.&\left.Z_{2}\left(t, e^{j \omega}\right) \quad \cdots \quad Z_{M}\left(t, \rho^{j \omega}\right)\right] \\
A^{T}\left(e^{j \omega}\right)=\left[A_{1}\left(e^{j \omega}\right)\right.& A_{2}\left(e^{j \omega}\right) \cdots \left.A_{M}\left(e^{j \omega}\right)\right] \\ 
N_{s}^{T}\left(t, e^{j \omega}\right)=\left[N_{1}^{s}\left(t, e^{j \omega}\right)\right.&\left.N_{2}^{s}\left(t, e^{j \omega}\right) \quad \cdots \quad N_{M}^{s}\left(t, e^{j \omega}\right)\right] \\ 
N_{t}^{T}\left(t, e^{j \omega}\right)=\left[N_{1}^{t}\left(t, e^{j \omega}\right)\right.&\left.N_{2}^{t}\left(t, e^{j \omega}\right) \quad \cdots \quad N_{M}^{t}\left(t, e^{j \omega}\right)\right] \end{aligned}$$

和$Z_{m}\left(t, e^{j \omega}\right), S\left(t, e^{j \omega}\right), N_{m}^{s}\left(t, e^{j \omega}\right), \text { and } N_{m}^{t}\left(t, e^{j \omega}\right)$是各自信号的短时傅里叶变换（STFT）。$A_m(e^{jw})$是第m个传感器ATF的频率响应，假设在分析期间是时不变的。

3  TF-GSC算法综述

　　Gannot等人提出了一种基于期望信号非平稳性的信号增强方法^[2]-[3]。M个麦克风信号通过M个滤波器进行滤波，$W_m^*(t,e^{jw});m=1,...,M$（* 表示共轭），并将其输出相加形成波束形成器输出

$$公式3：Y\left(t, e^{j \omega}\right)=W^{\dagger}\left(t, e^{j \omega}\right) Z\left(t, e^{j \omega}\right)$$

其中$\dagger$表示共轭转置，$W(t,e^{jw})$由下给出

$$\boldsymbol{W}^{T}\left(t, e^{j \omega}\right)=\left[W_{1}\left(t, e^{j \omega}\right) \quad W_{2}\left(t, e^{j \omega}\right) \quad \cdots \quad W_{M}\left(t, e^{j \omega}\right)\right]$$

$W(t,e^{jw})$是通过最小化输出功率来确定的，该输出的信号部分是期望信号$S(t,e^{jw})$，直到某个预先指定的滤波器$F^*(t,e^{jw})$（通常是简单的延迟）。通过构建如图1所示的GSC结构，可以有效地实现这种最小化。

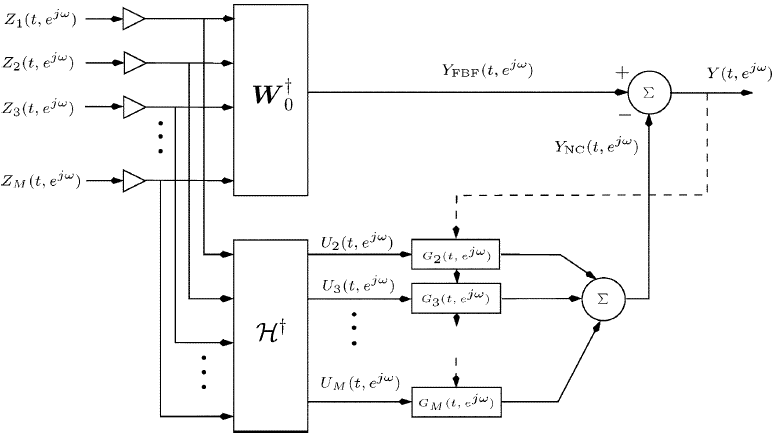
图1 通用TFs案例的GSC解决方案(TF-GSC)

　　GSC解决方案由三部分组成：由$W_0^{\dagger}$实现固定波束形成器（FBF），由$^{\dagger}(e^{jw})$实现块矩阵（BM），其构造噪声参考信号（包括静态和瞬态分量）和由滤波器$G(t,e^{jw})$实现的多通道噪声消除器（NC）。调整滤波器$G(t,e^{jw})$使输出$Y(t,e^{jw})$功率最小化，与经典的Widrow问题[17]完全相同。为了稳定更新算法，滤波器通常被约束在FIR结构上。

　　虽然对ATFs $A(e^{jw})$的精确了解会产生所需语音信号的无失真重建，但是已经证明，仅ATFs比$H(e^{jw})$在实践中就足够了。对ATFs ratio(比率)使用以下定义

$$H\left(e^{j \omega}\right)=\frac{A\left(e^{j \omega}\right)}{A_{1}\left(e^{j \omega}\right)}=\left[\begin{array}{ccc}{1} & {\frac{A_{2}\left(t, e^{j \omega}\right)}{A_{1}\left(t, e^{j \omega}\right)}} & {\cdots} & {\frac{A_{M}\left(t, e^{j \omega}\right)}{A_{1}\left(t, e^{j \omega}\right)}}\end{array}\right]$$

suboptimal(次优)的FBF块变为$W_0(t,e^{jw})=(\frac{H(e^{jw})}{||H(e^{jw})||^2})F(e^{jw})$。块矩阵$H(e^{jw})$也可以通过单独使用ATFs比率来确定^[2]。图2中总结了该算法，其中，假设ATFs比率向量是已知的。然而，在实践中$H(e^{jw})$是未知的，应该估计。我们使用一种基于期望信号非平稳性的估计方法。分析间隔被分成多个帧，这样期望的信号在每个帧中可以被认为是平稳的（语音信号的短时平稳性），而$H_m(e^{jw})$在整个分析间隔中仍然被认为是固定的。

1、TF-s ratios(比值)：$\boldsymbol{H}\left(e^{j \omega}\right)=\frac{\boldsymbol{A}\left(e^{j \omega}\right)}{A_{1}\left(e^{j \omega}\right)}$

2、构造分块矩阵，$\mathcal{H}^{\dagger}\left(e^{j \omega}\right) \boldsymbol{A}\left(e^{j \omega}\right)=0$

3、固定波束形成器 (FBF)$\mathcal{H}^{\dagger}\left(e^{j \omega}\right) \boldsymbol{A}\left(e^{j \omega}\right)=0$

　　FBF 输出$Y_{\mathrm{FBF}}\left(t, e^{j \omega}\right)=\boldsymbol{W}_{0}^{\dagger}\left(e^{j \omega}\right) \boldsymbol{Z}\left(t, e^{j \omega}\right)$

4、噪声参考信号$\begin{array}{l}{U\left(t, e^{j \omega}\right)=\mathcal{H}^{\dagger}\left(e^{j \omega}\right) Z\left(t, e^{j \omega}\right)=\mathcal{H}^{\dagger}\left(e^{j \omega}\right) \boldsymbol{N}\left(t, e^{j \omega}\right)} \\ {\left(\text { or } U_{m}\left(e^{j \omega}\right)=Z_{m}\left(t, e^{j \omega}\right)-\frac{A_{m}\left(e^{j \omega}\right)}{A_{1}\left(e^{j \omega}\right)} Z_{1}\left(t, e^{j \omega}\right) ; m=2, \ldots, M\right)}\end{array}$

5、输出信号$Y\left(t, e^{j \omega}\right)=Y_{\mathrm{FBF}}\left(t, e^{j \omega}\right)-G^{\dagger}\left(t, e^{j \omega}\right) \boldsymbol{U}\left(t, e^{j \omega}\right)$

6、过滤器更新，对于$m=1,....,M-1$

$${\tilde G_m}\left( {t + 1,{e^{j\omega }}} \right) = {G_m}\left( {t,{e^{j\omega }}} \right) + \mu \frac{{{U_m}\left( {t,{e^{j\omega }}} \right){Y^*}\left( {t,{e^{j\omega }}} \right)}}{{{P_{{\rm{est}}}}\left( {t,{e^{j\omega }}} \right)}}\;$$

$${G_m}\left( {t + 1,{e^{j\omega }}} \right)\quad {\hat G_m}\left( {t + 1,{e^{j\omega }}} \right)$$

$${P_{{\rm{est}}}}\left( {t,{e^{j\omega }}} \right) = \rho {P_{{\rm{est}}}}\left( {t - 1,{e^{j\omega }}} \right) + (1 - \rho )\sum\limits_m {{{\left| {{Z_m}\left( {t,{e^{j\omega }}} \right)} \right|}^2}} $$

7、根据重叠和保存方法[18]，只保留非锯齿样本。

图2 TF-GSC算法综述

定义$\Phi_{z_{i i} z_{j}}^{(k)}\left(e^{j \omega}\right)$为第$k$帧$(k=1,...K)$期间$z_i$和$z_j$（分别为第$i$和$j$次噪声信号观测）之间的交叉PSD（功率谱密度）。进一步定义$\Phi_{u_mz_1}(e^{j \omega})$为$u_m(t)$（第$m$个噪声参考信号）和$z_1(t)$之间的交叉PSD。让$\hat{\Phi}_{Z_{i i} j_{j}}^{(k)}\left(e^{j \omega}\right)$和$\hat{\Phi}^{(k)}_{u_mz_1}\left(e^{j \omega}\right)$表示相应的估计。将最小二乘法应用于下列超定方程组，得到$H_m(e^{jw})$的无偏估计

$$公式4：\begin{aligned} &\left[\begin{array}{c}{\hat{\Phi}_{z_{m} z_{1}}^{(1)}\left(e^{j \omega}\right)} \\ {\hat{\Phi}_{z_{m} z_{1}}^{(2)}\left(e^{j \omega}\right)} \\ {\vdots} \\ {\hat{\Phi}_{\hat{z}_{m} \tilde{z}_{1}}^{(K)}\left(e^{j \omega}\right)}\end{array}\right]=\left[\begin{array}{cc}{\hat{\Phi}_{z_{1} z_{1}}^{(1)}\left(e^{j \omega}\right)} & {1} \\ {\hat{\Phi}_{z_{1} z_{1}}^{(2)}\left(e^{j \omega}\right)} & {1} \\ {\vdots} & {} \\ {\hat{\Phi}_{z_{1} z_{1}}^{(K)}\left(e^{j \omega}\right)} & {1}\end{array}\right] \times\left[\begin{array}{c}{H_{m}\left(e^{j \omega}\right)} \\ {\Phi_{u_{m} z_{1}}\left(e^{j \omega}\right)}\end{array}\right]+\left[\begin{array}{c}{\varepsilon_{m}^{(1)}\left(e^{j \omega}\right)} \\{\varepsilon_{m}^{(2)}\left(e^{j \omega}\right)} \\ {\vdots} \\ {\varepsilon_{m}^{(K)}\left(e^{j \omega}\right)}\end{array}\right] \end{aligned}$$

其中，对每个麦克风信号$(m=2,...,M)$和频率指数$(e^{jw})$使用一组单独的方程，K是分析间隔内的帧数。要最小化的误差项由$\varepsilon _m^{(k)}(e^{jw})=\Phi_{u_mz_1}(e^{jw})-\hat{\Phi}_{u_mz_1}(e^{jw});k=1,...,K.$定义

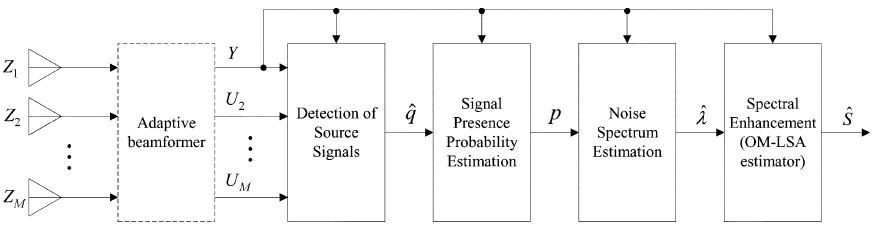
 图3 多麦克风后置滤波的框图

4  多麦克风后置滤波器

　　在这一部分中，我们讨论了在波束形成器输出端估计噪声PSD的问题，并提出了多麦克风后置滤波技术。图3描述了所提出的后置滤波方法框图。在波束形成器输出端，利用波束形成器输出端的瞬时功率Y与参考信号$\{U_k\}_{k=2}^M$处的瞬时功率之比，检测出所需的语音分量，然后导出先验语音缺失概率的估计$\hat{q}(t,e^{jw})$，基于高斯统计模型估计语音存在概率$p(t,e^{jw})$。然后，通过递归平滑波束形成器输出的周期图来估计噪声PSD，其中语音存在概率控制时变频率相关的平滑参数，以防止噪声估计由于语音成分而增加。最后，通过应用OM-LSA增益函数实现波束形成器输出的频谱增强，该增益函数最小化了log- spectrum(对数谱)[15]的均方误差。

　　设$S$为功率谱域中的smoothing operator(平滑算子)，定义为

$$公式5：\begin{aligned} \mathcal{S}Y\left(t, e^{j \omega}\right) &=\alpha_{s} \cdot \mathcal{S}Y\left(t-1, e^{j \omega}\right)+\left(1-\alpha_{s}\right) \sum_{\omega^{\prime}=-\Omega}^{\Omega} b\left(e^{j \omega^{\prime}}\right)\left|Y\left(t, e^{j\left(\omega-\omega^{\prime}\right)}\right)\right|^{2} \end{aligned}$$

$$公式6：\psi (t,e^{jw})=\frac{max \{{SY(t,e^{jw})-MY(t,e^{jw}),0\}}}{maax\{SU_m(t,e^{jw})-MU_m(t,e^{jw})\}_{m=2}^M,\varepsilon MY(t,e^{jw})}$$

其中$\alpha_s(0\leq \alpha_s\leq 1)$是时间平滑的遗忘因子，$b$是确定频率平滑顺序的归一化窗口函数$\sum_{w^{\prime}=-\Omega}^{\Omega} b\left(e^{j \omega^{\prime}}\right)=1$（$2\Omega $是频率带宽）。设$M$表示背景伪平稳噪声PSD的最小控制递推平均（MCRA）估计量[19]，[20]。然后，我们定义一个瞬态波束参考比（TBRR）[16]，如本页底部所示，其中是一个常数（通常$\varepsilon =0.01$），防止在参考信号处没有瞬态功率的情况下分母减小到零。这给出了波束形成器输出处的瞬态功率与参考信号处的瞬态功率之间的比率，这表明瞬态分量更可能来自语音或环境噪声。假设波束形成器的转向误差相对较低，并且干扰噪声与期望的语音不相关，如果瞬态与期望的源相关，则TBRR通常较高[21]。对于所需的源部件，波束形成器输出的瞬态功率明显大于参考信号的瞬态功率。因此，（6）中的名物比分母大得多。另一方面，对于干扰瞬态，TBRR小于1，因为至少一个参考信号的瞬态功率大于波束形成器输出的瞬态功率。通过修改基于TBRR的语音存在概率，我们可以产生一种非平稳噪声抑制的双重机制：首先，通过噪声估计的快速更新（噪声估计的增加实质上导致较低的谱增益）。其次，通过谱增益计算（谱增益被语音存在概率指数修正[15]）。

　　设$\gamma_{s}\left(t, e^{j \omega}\right) \triangleq\left|Y\left(t, e^{j \omega}\right)\right|^{2} / \mathcal{M} Y\left(t, e^{j \omega}\right)$表示波束形成器输出相对于伪平稳噪声的后验信噪比。那么，只有当$\gamma_{s}\left(t, e^{j \omega}\right)$和$\psi(t,e^{jw})$都很大时，才有可能出现语音。$\gamma _s(t,e^{jw})$的大值意味着波束形成器输出包含一个瞬态，而TBRR指示该瞬态是期望的还是干扰的。因此

$$公式7：\hat{q}\left(t, e^{j \omega}\right)=\left\{\begin{array}{ll}{1,} & {\text { 如果} \gamma_{s}\left(t, e^{j \omega}\right) \leq \gamma_{\text {low }}} {\text { 或者} \psi\left(t, e^{j \omega}\right) \leq \psi_{\text {low }}}
\\ {\max \left\{\frac{\gamma_{\text {high }-\gamma_{s}(t, e)^{j}}}{\gamma_{\text {high }-\gamma_{\text {low }}}}\right.} {\frac{\psi_{\text {ligh }}-\psi\left(t, e^{j \omega}\right)}{\gamma_{\text {low }}}} {\text { , }}{ \frac{\psi_{\text {high }}-\psi_{\text {low }}}{\psi_{\text {high }}-\psi_{\text {low }}}} & {, 0\}, \text { 其他}}\end{array}\right.$$

可以作为一个启发式表达式来估计先验语音缺失概率。它假设$\gamma _s(t,e^{jw})\leq \gamma _{low}$和$\psi(t,e^{jw})\leq \psi _{low}$都不存在语音。假设$\gamma _s(t,e^{jw})\leq \gamma _{high}$和$\psi(t,e^{jw})\leq \psi _{high}$都存在语音。常数$\psi _{low}$和$\psi _{high}$表示语音活动时在$\psi(t,e^{jw})$的不确定性，$\gamma _{low}$和$\gamma _{high}$表示与$\gamma _s(t,e^{jw})$相关的不确定性。在$\gamma _s\in [\gamma _{low},\gamma _{high}]$和$\psi \in[\psi_{low},\psi_{high}]$区域，我们假设$\hat{q}(t,e^{jw})$是$\gamma _s(t,e^{e^{jw}})$和$\psi(t,e^{jw})$的光滑双线性函数。

　　基于高斯统计模型[22]，语音persence(出现)概率由

$$公式8：p\left(t, e^{j \omega}\right)=\left\{1+\frac{q\left(t, e^{j \omega}\right)}{1-q\left(t, e^{j \omega}\right)}\left(1+\xi\left(t, e^{j \omega}\right)\right) \exp \left(-v\left(t, e^{j \omega}\right)\right)\right\}^{-1}$$

其中$\xi\left(t, e^{j \omega}\right) \triangleq E\left\{\left|S\left(t, e^{j \omega}\right)\right|^{2}\right\} / \lambda\left(t, e^{j \omega}\right)$为先验SNR，$\lambda (t,e^{jw})$为波束形成器输出处的噪声PSD（包括平稳和非平稳噪声分量），$\xi\left(t, e^{j \omega}\right) \triangleq \frac{\gamma (t,e^{jw})\xi (t,e^{jw})}{(1+\xi(t,e^{jw}))}$$\xi\left(t, e^{j \omega}\right) \triangleq \frac{|Y(t,e^{jw})|^2}{\lambda (t,e^{jw})}$为后验总SNR。先验信噪比的估计采用decision-directed(决策导向)方法(这是以Ephraim和Malah的决策导向估计的一个改进版本)[15]

$$公式9：\begin{aligned} \hat{\xi}\left(t, e^{j \omega}\right)=\alpha G_{H_{1}}^{2}\left(t-1, e^{j \omega}\right) \gamma\left(t-1, e^{j \omega}\right) +(1-\alpha) \max \left\{\gamma\left(t, e^{j \omega}\right)-1,0\right\} \end{aligned}$$

其中$\alpha$是控制噪声降低和信号失真之间的权衡的加权因子，以及

$$公式10：G_{H_{1}}\left(t, e^{j \omega}\right) \triangleq \frac{\xi\left(t, e^{j \omega}\right)}{1+\xi\left(t, e^{j \omega}\right)} \exp \left(\frac{1}{2} \int_{v\left(t, e^{j \omega}\right)}^{\infty} \frac{e^{-x}}{x} d x\right)$$

是语音一定存在时对数谱幅度（LSA）估计器的谱增益函数[23]。

　　波束形成器输出处的噪声估计是通过递归平均噪声测量的过去谱功率值来获得的。语音存在概率控制递归平均的速率。具体来说，噪声PSD估计由

$$公式11：\begin{aligned} \hat{\lambda}\left(t+1, e^{j \omega}\right)=\tilde{\alpha}_{\lambda}(&\left.t, e^{j \omega}\right) \hat{\lambda}\left(t, e^{j \omega^{\prime}}\right)+\beta \cdot\left[1-\tilde{\alpha}_{\lambda}\left(t, e^{j \omega}\right)\right]\left|Y\left(t, e^{j \omega}\right)\right|^{2} \end{aligned}$$

其中$\tilde{\alpha }_\lambda (t,e^{jw})$是时变频率相关的平滑参数，$\beta$是在语音不存在时补偿偏差的因子[19]。平滑参数由语音存在概率$p(t,e^{jw})$和表示其最小值的常数$\alpha_{\lambda}(0<\alpha_{\lambda}<1)$决定

$$公式12：\tilde{\alpha}_{\lambda}\left(t, e^{j \omega}\right) \triangleq \alpha_{\lambda}+\left(1-\alpha_{\lambda}\right) p\left(t, e^{j \omega}\right)$$

当存在语音时，$\tilde{\alpha}_{_\lambda }(t,e^{jw})$接近1，从而防止由于语音分量而导致噪声估计增加。在语音缺失和静止背景噪声或干扰瞬变的情况下，（6）中定义的TBRR相对较小（与$\psi_{low}$相比）。因此，先验语音缺失概率（7）增加到1，语音存在概率（8）减少到0。随着语音出现概率的降低，平滑参数变小，有利于噪声估计的快速更新。特别地，在（11）中的噪声估计能够管理瞬态和稳态噪声分量。它利用波束形成器输出信号和参考信号的功率比来区分瞬时干扰和期望语音成分。

　　最后给出了洁净信号STFT的估计

$$公式13：\hat{S}\left(t, e^{j \omega}\right)=G\left(t, e^{j \omega}\right) Y\left(t, e^{j \omega}\right)$$

其中

$$公式14：G\left(t, e^{j \omega}\right)=\left\{G_{H_{1}}\left(t, e^{j \omega}\right)\right\}^{p\left(t, e^{j \omega}\right)} \cdot G_{\min }^{1-p\left(t, e^{j \omega}\right)}$$

是OM-LSA增益函数，$G_{min}$表示无语音时增益的下限约束。图4总结了多通道后置滤波算法的实现。表II给出了8 kHz采样率下各参数的典型值。

 图4所示。多通道麦克风后置滤波算法

5 实验设计

　　在这一部分中，我们将提出的后置滤波算法应用于语音增强问题，并评估其性能。我们评估了算法在会议室场景和汽车环境中的性能，并将简单的单麦克风后置滤波器（MIXMAX和OM-LSA）与更复杂的多麦克风算法进行了比较。

A 测试场景

　　对于会议室，研究了图5所示的场景。围墙是一个尺寸为5米×4米×2.8米的会议室，在房间中央的一张桌子上放置了一个线性阵列。使用了两个扬声器。一个用于语音源，另一个用于噪声源。它们的位置和四个麦克风的位置如图5的左侧所示。图的右侧描绘了从语音源到第一个麦克风的脉冲响应。该响应是使用输入信号源和接收到的麦克风信号（响应包括扬声器）之间的最小二乘拟合来获得的。我们注意到，在我们所有的实验中，我们使用了实际的记录，而没有使用估计的脉冲响应。

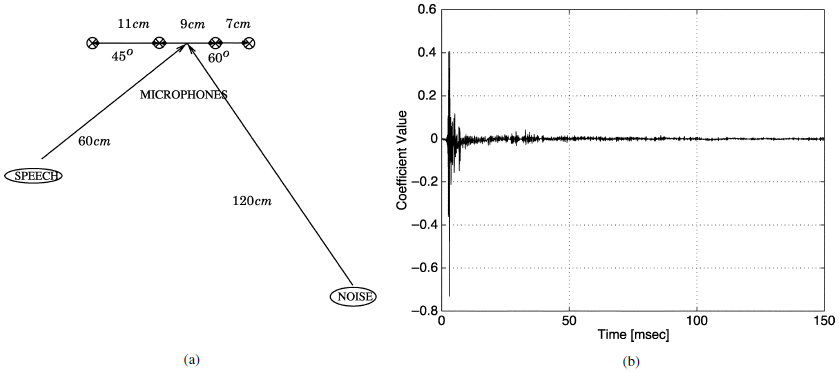
 图5  测试场景（a）在一个嘈杂的会议室里有四个麦克风。(b)从语音源到一号麦克风的脉冲响应

　　该语音源由来自德州仪器和麻省理工学院(TIMIT)数据库[24]的四句话组成，具有不同的增益级别，如图6左侧所示。麦克风信号的输入是通过混合语音和噪声成分产生的，这些成分是在不同的信噪比水平下分别在麦克风上测量产生的。我们考虑了三个噪声源。第一个是点噪声源。第二种是扩散噪声源，第三种是非平稳扩散噪声源。为了产生点噪声源，我们通过扬声器传输了一个实际的风扇噪声记录(低通PSD)。基于Dal-Degan和Prati[25]方法，模拟了平面PSD带通滤波噪声信号的全向发射，得到了扩散噪声源。第三种是相同的扩散噪声源，但具有交变振幅，以证明该算法处理噪声信号中的瞬态的能力。

　　汽车场景通过实际的(单独的)语音信号录音和汽车噪声信号进行测试，语音信号由10个英语数字组成，如图6右侧所示。汽车的窗户微微开着。过路的汽车和吹来的风会产生短暂的噪音。噪音的固定成分来自于道路的持续嗡嗡声。四个麦克风安装在侧面转向配置的遮阳板。麦克风信号由不同信噪比的语音和噪声信号混合产生。

 图6 干净的语音信号。(a)会议中有4个TIMIT句子，(b) car中有10个英文数字。

B 算法的参数

　　整个系统的采样率为8千赫。在TF-GSC算法中，使用了以下参数。分块滤波器$H_m(e^{jw})$由非因果FIR-s建模，在区间[90,89]内具有180个系数。对消除滤波器$G_m(e^{jw})$由区间为250的非因果FIR-s建模[125，124]。为了实现重叠和保存过程，使用了512个样本的片段。对于会议室环境，系统识别程序使用13个片段，每个片段1000个样本。在汽车环境中，有8个部分，500个部分被证明是足够的。我们注意到，系统辨识只适用于主动语音周期，而噪声保持平稳特性。然而，准确的语音活动检测器（VAD）不是必要的。

　　应用了三种后过滤程序，即MIXMAX、OM-LSA和多麦克风。

　　对于MIXMAX算法[13]，[14]，帧长度被设置为L＝256（50%重叠），这对应于K＝129个相关的频箱。用于限制噪声抵消器增益的阈值被设置为$\delta _k=0.35$（对于$0\leq k\leq 36$）和$\delta _k=0.18$（对于$37\leq k\leq 128$），即算法增益被每个频bin中给定的G值限制。

　　对于OM-LSA算法，STFT使用256个样本长度(32 ms)的Hamming窗口和64个样本帧更新步骤(75%重叠帧)实现。利用改进的决策导向方法估计先验信噪比，$\alpha=0.92$。光谱增益被限制在最小20 dB，噪声PSD被估计使用改进的MCRA技术[19]。用于估计先验语音缺失概率的参数值汇总在表一中(估计器及其参数在[15]中描述)。

表1 OM-LSA算法用于先验语音缺失概率估计的参数取值

　　多麦克风后过滤参数如表二所示。

表二 所提出的多麦克风后置滤波实现中的参数值

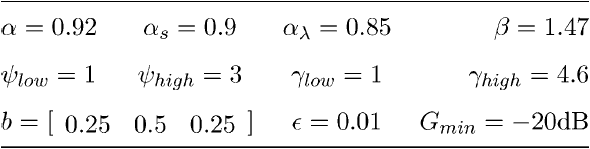
C 客观评价

　　采用三个客观质量指标对算法性能进行了评价。

　　第一个客观的质量测量是在非活动语音期间的噪声水平(NL)，定义为

$$NL=Mean_t\{10\log_{10}(E(t),t\in Speech\quad Nonactive)\}$$

其中$E(t)=\sum_{\tau \in T_t}y^2(\tau ),y(t)$是要评估的信号（噪声信号或算法的输出），$T_t$为segment(段号)$t$对应的时间实例。注意，NL图越低，通过相应算法得到的结果越好。

　　第二个优点是加权节段信噪比(W-SNR)。该方法对频带内的节段信噪比进行加权。频带与耳临界频带成比例间隔，权值根据语音感知质量进行构造。

　　设$z_{1,s}(t)=\alpha_1(t)*s(t)$为第一个麦克风中的仅语音部分，$y(t)$为要评估的信号。进一步定义，$Z_{1,s}(t,B_k)$和$Y(t,B_k)$是$B_k$频段的相应信号。现在，定义$SNR(t,B_k)=\frac{\sum_{\tau \in T_t}Y^2(\tau ,B_k)}{\sum_{\tau \in T_t}(Y(\tau ,B_k)-Z_{1,s}(\tau,B_k))^2}$段数$t$和频带$B_k$中的SNR。W-SNR定义为

$$\begin{array}{l}{\mathrm{W}-\mathrm{SNR}}{=\mathrm{Mean}_{\mathrm{t}}\left\{10 \log _{10}\left(\sum_{\mathrm{k}} \mathrm{W}\left(\mathrm{B}_{\mathrm{k}}\right) \mathrm{SNR}\left(\mathrm{t}, \mathrm{B}_{\mathrm{k}}\right), \mathrm{t} \in \text { Speech Active }\right)\right\}}\end{array}$$

频带$B_k$及其对应的重要性权重$W(B_k)$按ANSI标准[26]。研究表明，与经典信噪比或分段信噪比相比，W-SNR测量与听者感知到的质量概念更密切相关。

　　第三个与平均意见评分(MOS)相关性较好的客观语音质量度量是由

$$\begin{array}{l}{\text { LSD }} {\text { = Meant }\{\sqrt{\left.\operatorname{Mean}_{\omega}\left\{\left[20 \log _{10}\right] \mathrm{S}\left(\mathrm{t}, \mathrm{e}^{\mathrm{j} \omega}\right)\left|-20 \log _{10}\right| \mathrm{Y}\left(\mathrm{t}, \mathrm{e}^{\mathrm{j} \omega}\right) |\right]^{2}\right\}}} \quad {t \in \text { Speech Active }\}}\end{array}$$

回想一下，$S(t,e^{jw})$和$Y(t,e^{jw})$分别是输入信号和评估信号的STFT。注意，较低的LSD级别对应于较好的性能。

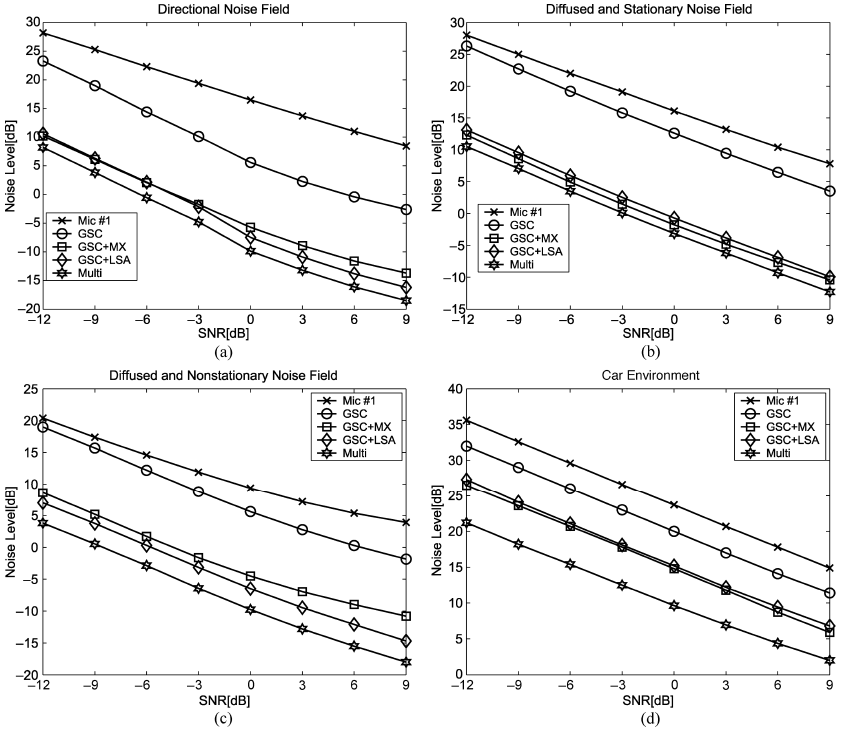
 图7 非主动语音期间的平均噪声水平(NL)

　　四种噪声条件下的NL值如图7所示。从图7可以看出，对于每个噪声源，使用多麦克风后置滤波器得到的残差噪声水平最低。在平稳噪声的情况下，两种单通道后置滤波器(MIXMAX和OM-LSA)的性能是相当的，尽管与多麦克风后置滤波器有关，它们的性能有所下降。因此，用多麦克风后过滤代替单麦克风后过滤的优点就不那么明显了。TF-GSC波束形成器在方向性噪声源中取得了较好的效果，因此所有后置滤波的作用不如扩散噪声场中的作用重要。

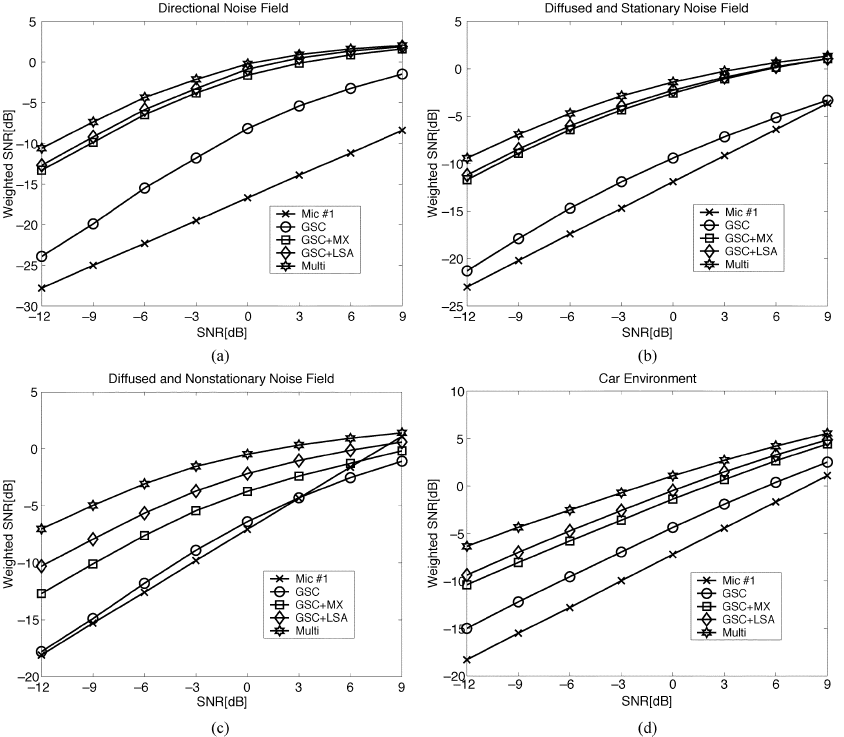
 图8 主动语音期间的平均加权信噪比

　　图8给出了W-SNR的结果。同样，一般来说，使用多麦克风后置滤波器可获得最佳性能（最高W-SNR）。其重要性在非平稳噪声（非平稳扩散噪声和汽车噪声）情况下更为明显。在定向（和静止）噪声场中，MIXMAX后置滤波器和多麦克风后置滤波器的性能几乎相同。然而，TF-GSC在没有任何后置滤波的情况下取得了很好的效果。LSD结果如图9所示。很明显，LSD质量度量的结果与前面的讨论是一致的。

 图9  活跃语音期间的平均LSD

　　跟踪LSD和W-SNR优点随时间的变化也很有趣。在图10中，给出了汽车噪声情况下两种质量测量方法的轨迹。为了方便起见，图中还描述了VAD决策。结果表明，在TF-GSC输出中使用多麦克风后置滤波器可以提高性能。在非活动演讲期间，这两种质量测量方法的改善尤其令人印象深刻。

图10 汽车噪音的LSD和W-SNR痕迹

D 主观评价

　　主观质量评价是对超声图像的评价。从图11所示的声像图中可以得出一些观察结果。在$t=2.5$[s]和$t=4$[s]之间存在具有宽频率成分的噪声信号（由于超车）。波束形成器不能单独处理这种非平稳噪声。虽然单传声器后置滤波器降低了噪声水平，但只有多传声器后置滤波器能给出令人满意的结果。$t=4.2$[s]和$t=5.5$[s]之间存在风吹（低频成分）。多传声器后置滤波器并不能完全消除这种干扰，但其性能优于其他算法。从声像图上也可以看出该算法的低失真。

　　非正式的听力测试证实了这些结论。处理过的语音信号的例子可以在[27]找到。

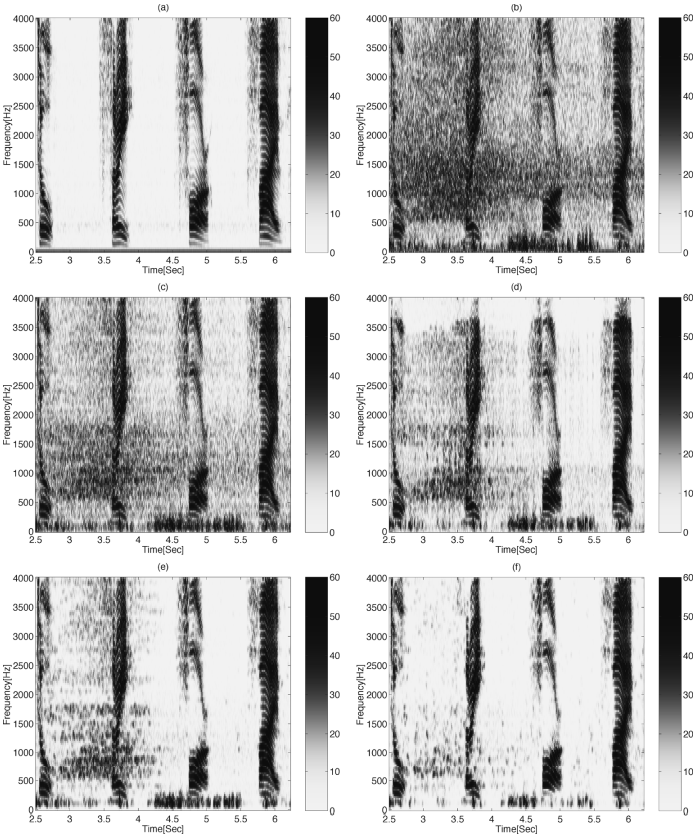
图11（a）清洁汽车信号的声像图（b）麦克风1处有噪声信号（c）TF-GSC

（d）TF-GSC+MIXMAX（e）TF-GSC+OM-LSA（f）微型多麦克风后置滤波器

6 总结

　　多麦克风阵列常用于语音增强应用。众所周知，这些阵列的预期性能有一定的局限性，特别是当噪声场趋于扩散时。在汽车车厢中通常假定存在扩散噪声场。为了进一步降低波束形成器输出的噪声，提出了几种后置滤波方法。两种方法在TF-GSC波束形成器的输出端使用现代单麦克风语音增强器。即使用之前提出的MIXMAX和OM-LSA算法。作为一种替代方法，一种新的多麦克风后过滤被纳入TF-GSC。后一种方法利用TF-GSC中构造的噪声参考信号来改进噪声估计。所有的后置滤波方法都是通过客观(降噪、加权节段信噪比和对数光谱距离)和主观质量测量(声波图和非正式听力测试)来评估的。所有后置滤波器都提高了组合系统的降噪效果，特别是在扩散噪声领域。但是，在保持TF-GSC主输出的低语音失真的同时，多麦克风后置滤波器的降噪效果最好。这一优点在非平稳噪声环境中得到了强调，在非平稳噪声环境中，改进后的噪声估计可以得到更强的体现。

参考文献

作者简介：

Sharon Gannot (S 92 M 01)于1986年获得以色列海法以色列理工学院的理学学士学位(4)，并于1995年和2000年分别获得以色列特拉维夫大学的理学硕士学位(以优等成绩获得)和博士学位，均为电子工程专业。从1986年到1993年，他是以色列国防军的研发负责人。2001年，他在比利时鲁汶Katholieke Universiteit (ku)的电气工程系(SISTA)担任博士后。2002年至2003年，他在以色列理工学院电子工程学院信号与图像处理实验室(SIPL)从事研究和教学工作。目前，他是以色列巴伊安巴伊兰大学工程学院的讲师。他的研究兴趣包括参数估计，统计信号处理，语音处理，使用单个或多麦克风阵列。他是Eurasip应用信号处理杂志的副主编。

Israel Cohen (M 01 SM 03)分别于1990年、1993年和1998年在以色列海法的以色列理工学院(Technion Israel Institute of Technology)获得理学士(Summa Cum Laude)、理学士(M.Sc.)和电气工程博士学位。

　　从1990年到1998年，他是以色列国防部海法拉斐尔研究实验室的一名研究科学家。从1998年到2001年，他是耶鲁大学计算机科学系的博士后研究员。自2001年以来，他一直是以色列Technion电子工程系的高级讲师。他的研究兴趣包括统计信号处理、声学信号分析和建模、语音增强、噪声估计、麦克风阵列、源定位、盲源分离、系统辨识和自适应滤波。

　　科恩博士是《IEEE语音和音频处理学报》和《IEEE信号处理快报》的副主编。