python数学模型 python实现数学模型(插值、拟合和微分方程)

时间:2021-03-15 ManTou馒头人气:0

想了解python实现数学模型(插值、拟合和微分方程)的相关内容吗，ManTou馒头在本文为您仔细讲解python数学模型的相关知识和一些Code实例，欢迎阅读和指正，我们先划重点：python数学模型,python插值拟合，下面大家一起来学习吧。

问题1 车辆数量估计

题目描述

交通管理部门为了掌握一座桥梁的通行情况，在桥梁的一端每隔一段不等的时间，连续记录1min内通过桥梁的车辆数量，连续观测一天24h的通过车辆，车辆数据如下表所示。试建立模型分析估计这一天中总共有多少车辆通过这座桥梁。

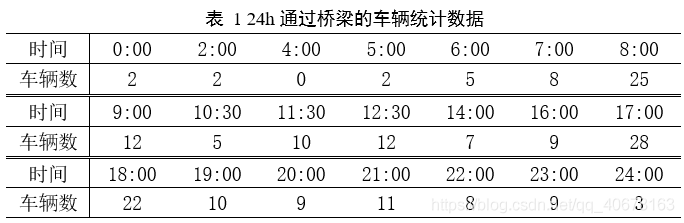
在这里插入图片描述

python 实现(关键程序)

def get_line(xn, yn):
    def line(x):
        index = -1
        # 找出x所在的区间
        for i in range(1, len(xn)):
            if x <= xn[i]:
                index = i - 1
                break
            else:
                i += 1
        if index == -1:
            return -100
        # 插值
        result = (x - xn[index + 1]) * yn[index] / float((xn[index] - xn[index + 1])) + (x - xn[index]) * yn[
            index + 1] / float((xn[index + 1] - xn[index]))
        return result
    return line
time = [0, 2, 4, 5, 6, 7, 8,
    9, 10.5, 11.5, 12.5, 14, 16, 17,
    18, 19, 20, 21, 22, 23, 24]
num = [2, 2, 0, 2, 5, 8, 25,
    12, 5, 10, 12, 7, 9, 28,
    22, 10, 9, 11, 8, 9, 3]
# 分段线性插值函数
lin = get_line(time, num)
# time_n = np.arange(0, 24, 1/60)
time_n = np.linspace(0, 24, 24*60+1)
num_n = [lin(i) for i in time_n]
sum_num = sum(num_n)
print("估计一天通过的车辆：%d" % sum_num)

结果

在这里插入图片描述

问题2 旧车平均价格

题目描述

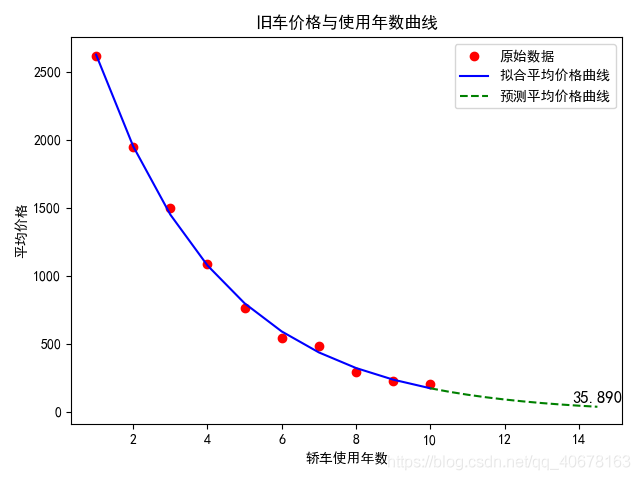
某年美国旧车价格的调查资料如下表所示，其中 x i x_i xi表示轿车的使用年数， y i y_i yi表示相应的平均价格。试分析用什么形式的曲线拟合表中所给的数据，并预测使用4.5年后轿车的平均价格大致为多少?

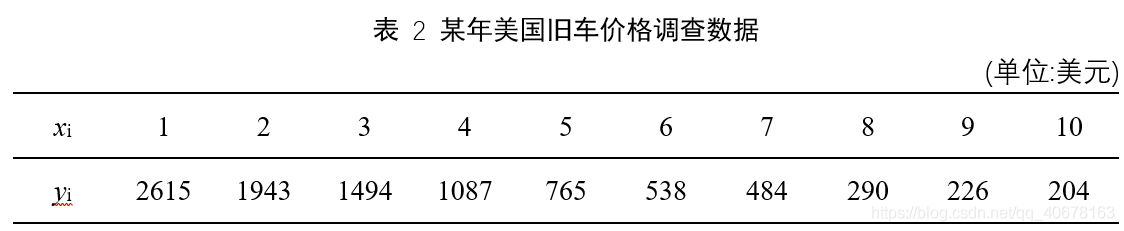
在这里插入图片描述

Python 实现(关键程序)

from scipy.optimize import curve_fit
def func(x, a, b, c): # 指数函数拟合
  return a * (b**(x-1)) + c

year = np.arange(1, 11, 1)
price = [2615, 1943, 1494, 1087, 765, 538, 484, 290, 226, 204]

popt, pcov = curve_fit(func, year, price)
a = popt[0]
b = popt[1]
c = popt[2]
price_fit = func(year, a, b, c)

结果

在这里插入图片描述

问题3 微分方程组求解

题目描述

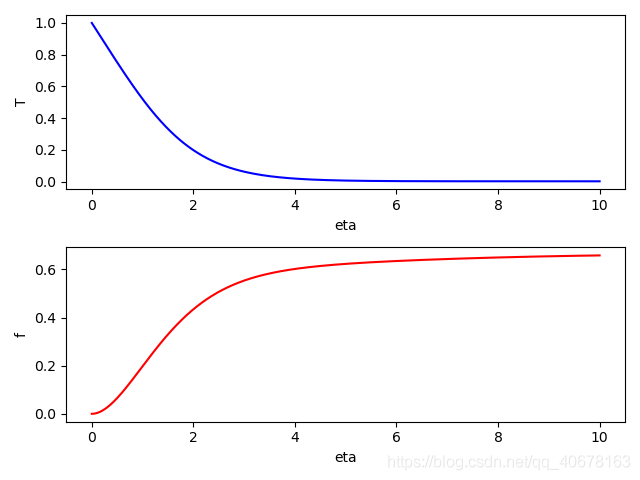
求下列微分方程组(竖直加热板的自然对流)的数值解

Python实现(关键程序)

from scipy.integrate import solve_ivp
def natural_convection(eta, y): # 将含有两个未知函数的高阶微分方程降阶，得到由2+3个一阶微分方程组成的方程组
  T1 = y[0]
  T2 = y[1]
  f1 = y[2]
  f2 = y[3]
  f3 = y[4]
  return T2, -2.1*f1*T2, f2, f3, -3*f1*f3 + 2*(f2**2)-T1

eta = np.linspace(0, 10, 1000)
eta_span = [0, 10]
init = np.array([ 1, -0.5, 0, 0, 0.68])

curve = solve_ivp(natural_convection, eta_span, init, t_eval=eta)

结果

在这里插入图片描述

问题4 野兔数量题目描述

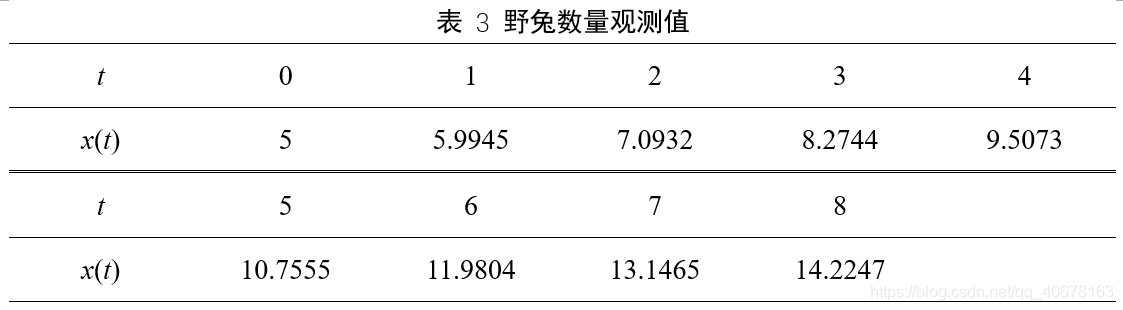
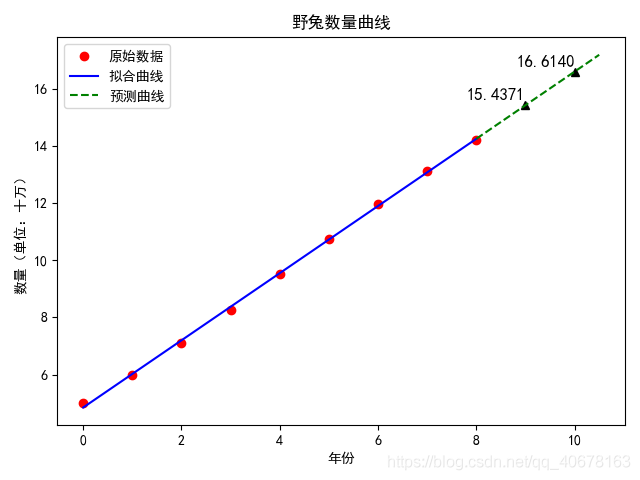
某地区野兔的数量连续9年的统计数量(单位:十万)如下表所示.预测t = 9, 10时野兔的数量。

在这里插入图片描述

Python实现(关键程序)

import numpy as np

year = np.arange(0, 9, 1)
num = [5, 5.9945, 7.0932, 8.2744, 9.5073, 10.7555, 11.9804, 13.1465, 14.2247]

fit = np.polyfit(year, num, 1)
print("线性拟合表达式：", np.poly1d(fit))
num_fit = np.polyval(fit, year)
plt.plot(year, num, 'ro', label='原始数据')
plt.plot(year, num_fit, 'b-',label='拟合曲线')
year_later = np.arange(8, 11, 0.5)
num_fit_curve = fit[0] * year_later + fit[1]

结果

在这里插入图片描述

加载全部内容