高等数学学习笔记

Part 1: 极限

• 设函数f(x)在点\(x_0\)的某一去心邻域内有定义，如果存在常数A，对于任意给定的正数ε（无论它多么小），总存在正数\(δ\)，使得对于\[0<|x-x_0|<δ\]，均有\[f(x)-A<ε\]

• 那么常数A就叫做函数f(x)当时\(x→x_0\)的极限，记作

\[ \lim_{x\to x_0}f(x) = A \]

夹逼定理

在求函数\(f(x)\)的极限时，可以通过两个函数夹它

举例：\(\lim_{x\to 0}\frac{sum(x)}x = 1\)

易知\(sin(x) < x < tan(x)\), 得\(cos(x) < \frac{sin(x)}x < 1\)

因为\(\displaystyle\lim_{x\to 0} cos(x) = 1,1=1\), 所以原式得证

Part 2: 导数

• 斜率：对于一次函数\(y=kx+b\)斜率即为k。

• 导数：通俗的说函数在一点的导数为在该处做切线，所得直线的斜率

\[ \large{f'(x_0)=\lim_{\delta x \to 0}}\frac{f(x_0+\delta x) - f(x_0)}{\delta x} \]

• 也可记做\(\frac{dy}{dx}\)

• 将原函数y(x)每个点的导数全部算出后形成一个新的函数叫做原函数的导函数\(y'(x)\)

• 高阶导记作 \(f^{(n)}\)

可导: 　从左侧与右侧趋近极限相同时才可定义导数

导数表：

导数与函数单调性

众所周知, 导数和函数单调性有着不可分割的关系

• 一阶导数描述增减, 一阶导等于零时, 原函数处于区间最值
• 二阶导数描述一阶导数增减, 描述原函数的凹凸性

导数公式

四则运算:
\[ (u \pm v)' = u' \pm v'\\(uv)'= u'v + v'u\\(\frac uv)'=\frac{(u'v-v'u)}{v^2}\\(C \cdot f(x))'=C \cdot f'(x) \\(f(g(x)))'=f'(g(x)) \cdot g'(x) \]
求导练习题

• \((2x^2-3ln(x))' = 4x-\frac 3x\)
• \(((x^2+1)(x +2))' = (x^2+1)(1)+(2x)(x+2)=3x^2+4x+1\)
• \((sin(3x+2))'=sin'(3x+2)(3x)=3x\cdot cos(3x+2)\)

Part 3: 洛必达法则：

若\(f(x)\)和\(g(x)\)在a点处为零
\[ \large{\lim_{x \to a}\frac{f(x)}{g(x)} = lim_{x \to a}\frac{\frac{f(x)-f(a)}{x-a}}{\frac{g(x)-g(a)}{x-a}}=\lim_{x \to a}\frac{f'(x)}{g'(x)}} \]
洛必达法则可以多次使用, 即多次求导

Part4: 自然对数e:

\[ \large{e=\lim_{n \to \infty}(1+\frac1n)^n=2.718281828459\cdots} \]

奇妙的性质:
\[ f(x) = e^x~~~f'(x) = e^x\\f(x) =ln~x ~~~f'(x)=\frac 1x \]

Part5: 寻找方程的根: 牛顿迭代法

找方程的根首先我们可以随机两个点, 使用勘根定理, 如果\(f(a)\cdot f(b) \leq 0\)则在区间\([a, b]\)内二分.

但是我们可能并不能很好的找到根所在的区间, 于是牛顿迭代法应运而生

求解方程\(f(x)=0\), 随机一个初始点

• 对于当前点x，做切线(求导)，计算与x轴交点作为下一轮迭代的x

• 可得\(x_{next}=x-\frac{f(x)}{f’(x)}\)

• \(f(x)<eps\)时终止，对于大部分函数有效(反例\(y=\frac1x 或~y=\sqrt {|x|}\))

Part6: 定积分

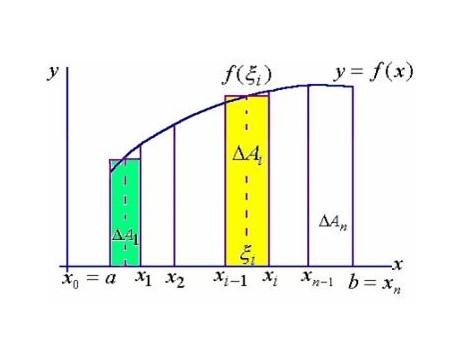
• 求函数\([a,b]\)区间里的有向面积，在x轴上方为正，x轴下方为负。

• 极限法：将区域切成无数细长条，每一长条用矩形面积\(f(x)*dx\)近似

\[ S = \int_a^bf(x)dx \\=\lim_{n \to \infty}\sum_{0<k\leq n}f(x_{k-1})*(x_k-x_{k-1})\\=\lim_{n \to \infty}\sum_{0<k\leq n}f(x_{k})*(x_k-x_{k-1}) \]

例: 求定积分\(\int_0^cx^2dx= \displaystyle \lim_{n \to \infty}x_k^2dx\)

\[ 原式=\lim_{n \to \infty}(\frac{ck}n)^2(\frac cn)\\=\lim_{n \to \infty}(\frac{c^3}{n^3})\sum_{0 \leq k<n}k^2\\=\lim_{n \to \infty}\large{(\frac{c^3(2n^3-3n^2+n)}{6n^3})}\\=\frac {c^3}3 \]

一般形式: \(\displaystyle \int_0^cx^ndx=\frac{c^{n+1}}{n+1}\)

积分与微分

积分与微分可以感性的理解为升维与降维, 所以它们天生有着妙不可言的关系:
\[ f'(x)dx=\lim_{n \to \infty}\sum_{0 \leq k < n}f(x_k)'dx\\=\lim_{n \to \infty}\sum_{0 \leq k < n}\large{\frac{f(x_{k+1})-f(x_k)}{(x_{k+1}-x_k)}(x_{k+1}-x_k)}\\=\lim_{n \to \infty}\sum_{0 \leq k < n}f(x_{k+1})-f(x_k)\\=\lim_{n \to \infty}f(x_{n-1})-f(x_0)=f(b)-f(a) \]

积分与无穷向量

对于一个函数\(f(x)\)可以理解为一个无穷维的向量，每个点的函数值是一个维度，那么两个函数\(f(x)\)和\(g(x)\)的内积就可以理解为\(\int f(x)g(x)dx\)

Part 7: 自适应Simpson积分法

前置:求二次函数区间内的有向面积;

• 见定积分基本内容

二次函数拟合积分法:
\[ \int^b_af(x)dx \approx \frac{b-a}6(f(a)+4f(\frac{a+b}2)+f(b) \]
可以使用自适应法控制精度问题

inline double simpson(double a, double b) {
    return (b - a) * (f(a) + f(b) + 4 * (f(((a+b)/2)))) / 6;
}

double eps = 1e-6;
double solve(double l, double r, double A, double eps) {
    double mid = (l + r) / 2;
    double L = simpson(l, mid), R = simpson(mid, r);
    if (fabs(L+R-A) <= 15 * eps) return L + R + (L+R-A) / 15.0;
    return solve(l, mid, L, eps / 2) + solve(mid, r, R, eps / 2);
}

应用: 在求解计算几何中的面积问题时

可以建立坐标系, 将面积化为一个函数, 求圆等圆滑的图形, 函数是平滑的, 但积分法无法解决一段函数全为零的情况, 所以提前判断有值的两端端点进行积分

Part8:函数最优化

给定多元函数\(f(x) \to R\), 求f(x)最小值

爬山法, 随机方向, 随机步长, 只向更优解走

如果函数存在导数, 有更好的方法, 如\(f(x)=sin(x_1)cos(x_2)\)

求偏导 :相当于定住其他变量, 求单一变量的导数

• 对于二元函数\(f(x,y)\)，在\((x_0,y_0)\)处固定y不变切片移动x，可以得到一个单变量函数\(g(x)\)，同理固定x不变可以得到\(h(y)\)，可以定义某一个方向的导数

• 求导时只需将另一个变量当做常数即可。

偏导练习

• \((x^2+1)(y+2)\)
• \(\large{\frac{sin^2(\frac3y)+ln(cos ~xy)}{x^5e^y}}\)

偏导数与梯度

• 梯度：\(\delta f(x,y)= (\frac{\delta f}{\delta x}, \frac{\delta f}{\delta y})\)

• 函数值上升最快的方向？

  \(f(x + dx, y + dy) \approx f(x, y) + \frac{\delta f}{\delta x}dx+\frac{\delta f}{\delta y}dy\)

• 单位圆上寻找\((dx,dy)\)使得其与梯度的内积最大

• 显然\((dx,dy)\)与梯度共线时增长最快

无约束函数极值

给定多元函数\(f(x)→R\)，其中x是n维向量，寻找使得函数值最小的向量x*。

代入偏导数为0的极值条件解方程：\(\delta f(x)=0\)

如: 求\(min f(x) = (x_1-x_2-2)^2+(x_2-1)^2\)
\[ \delta f(x) = \large\left(^{\frac{\delta f}{\delta x_1}}_{\frac{\delta f}{\delta x_2}}\right)= \left( ^{~~~~~~~~2(x_1-x_2-2)}_{-2(x_1-x_2-2)+2(x_2-1)}\right) = \left(^0_0\right) \]

Part 9: 拉格朗日乘数法

设给定多元函数\(ƒ(x)\)和附加条件\(\phi(x)=0\)，x为向量，为寻找z=ƒ(x)在附加条件下的极值点，构造拉格朗日函数\(L(x, \lambda)=f(x)+\lambda\phi(x)\)

此时有：
\[ \min_x=\min_x\{\max_{\lambda}L(x, \lambda)\}=\min_x\{\max_{\lambda}f(x)+\lambda\phi(x)\} \]

f(x)为最优的必要条件是拉格朗日函数L梯度为0：

由上述方程组解出x，就是函数z=ƒ(x)在附加条件φ(x)=0下可能的极值点。

例：求(x,y,z)使得\((x-4)^2+y^2+z^2\)最小，并且\(x+y+z=3, 2x+y+z=4\)

Part10: 泰勒展开

\[ f(x) = a_0 + a_1(x - x_0) + a_2(x - x_0)^2 + a_3(x - x_0)^3 + ...\\f(x) \approx f(0) + \frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\cdots+\frac{f^{(n)}}{n!}x^n \]

n趋于正无穷时, 将几乎完全拟合

证明:

\[ f(x) - f(0) = \int_0^{x}f'(x)dx\\f'(x) - f'(0)=\int_0^xf''(x)dx\\f(x) = f(0) + \int_0^{x}f'(x)dx\\= f(0) + \int_0^{x}\left(\int_0^xf''(x)dx + f'(0)\right)dx\\= f(0) + \int_0^{x}\int_0^xf''(x)dx^2 + \int_0^xf'(0)dx\\= f(0) + \int_0^{x}\int_0^xf''(x)dx^2 + \frac{f'(0)}{1!}x \]

将二次导, 三次导等带入即可用数学归纳法证明

常见泰勒展开

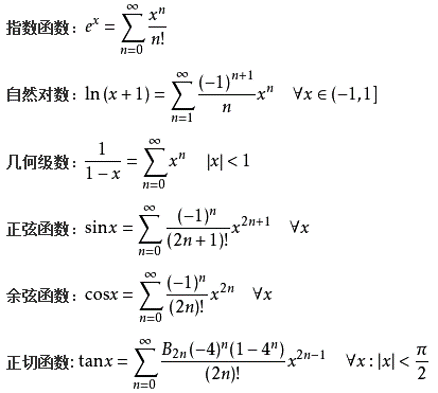
欧拉公式: \(e^{i\theta}=cos(\theta)+isin(\theta)\)

可用泰勒展开证明