机器学习算法概述

机器学习分类

• 监督学习：传统意义上的机器学习，即训练数据有标签，机器在学习过程中是有反馈的，知道正确与否；
• 无监督学习：与监督学习相反，没有标签，也没有反馈，只能从数据本身去挖掘，寻找规律；
• 强化学习：通过与环境进行交互获得的奖赏指导行为，目标是使智能体获得最大的奖赏；
• 半监督学习：顾名思义，介于监督学习和无监督学习之间；
• 深度学习：通过多层神经网络提取特征，提取特征数量大种类多，再根据反馈去调整网络参数。

python的机器学习库sklearn

1.自带数据集：

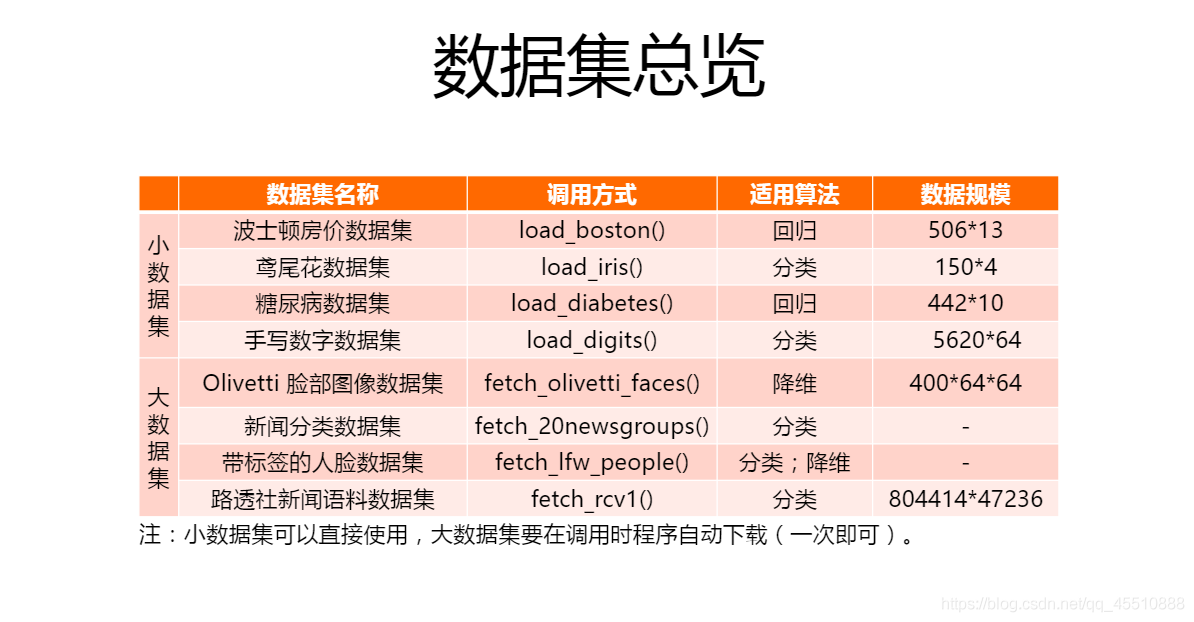
2.sklearn的主要功能：

功能	算法
聚类	K均值聚类K-means、DBSCAN、高斯混合模型GMM、BRICH、谱聚类、AP聚类、均值漂移、层次聚类
降维	主成分分析PCA、独立成分分析FastICA、非负矩阵分解NMF、LDA、字典学习、因子分析
分类	k邻近kNN、支持向量机SVM、朴素贝叶斯naivebayes、决策树、集成方法、MLP
回归	普通线性回归、岭回归、Lasso回归、弹性网络、最小角回归、贝叶斯回归、逻辑回归、多项式回归
模型选择	略
数据预处理	略

常用算法

1.无监督学习

无监督学习一般分为聚类和降维

（1）聚类（clustering）：对无标签的一组数据进行聚类，通过其“相似度”，也就是“距离”进行分类，通常分类的类别数是可以调整的。

距离包括

• 欧氏距离（传统的平面几何距离，可拓展到高维空间）
• 曼哈顿距离（街区距离）
• 马氏距离（协方差距离）
• 夹角余弦距离（向量的相似度）

算法

• K-means：随机找k个点作为初始聚类中心；对于剩下的点，以此计算其余点与聚类中心的距离（上面提到的，通常为高维空间），根据其与聚类中心的距离，归入最近的簇；对每个簇，计算所有点的均值作为新的聚类中心；重复以上步骤，直到聚类中心不发生改变。

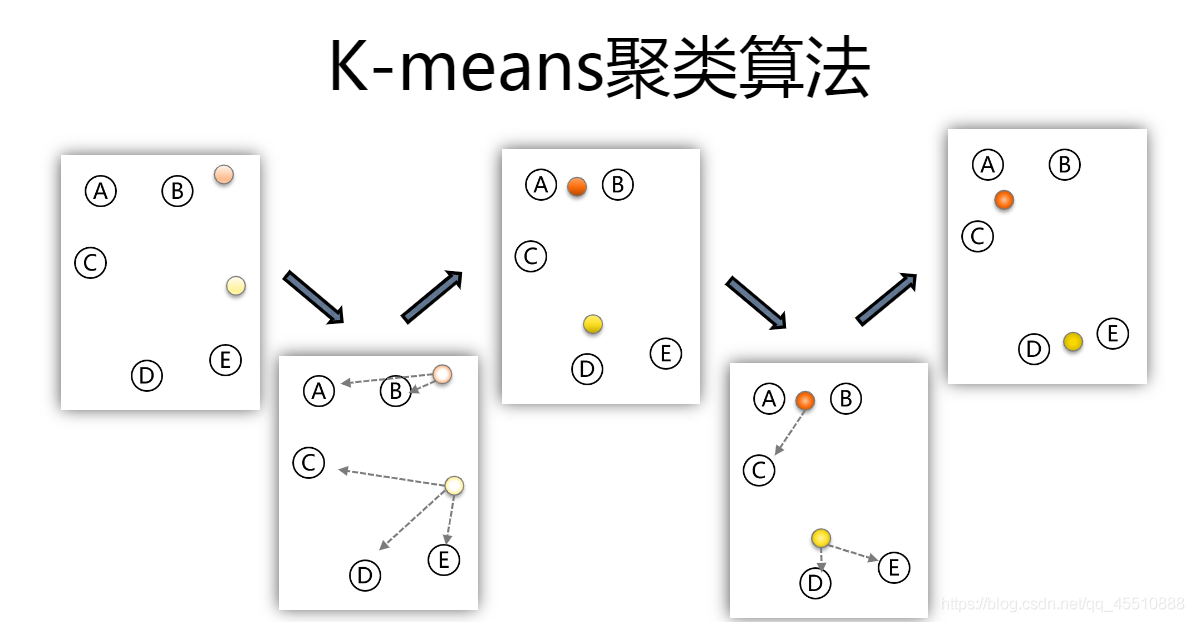
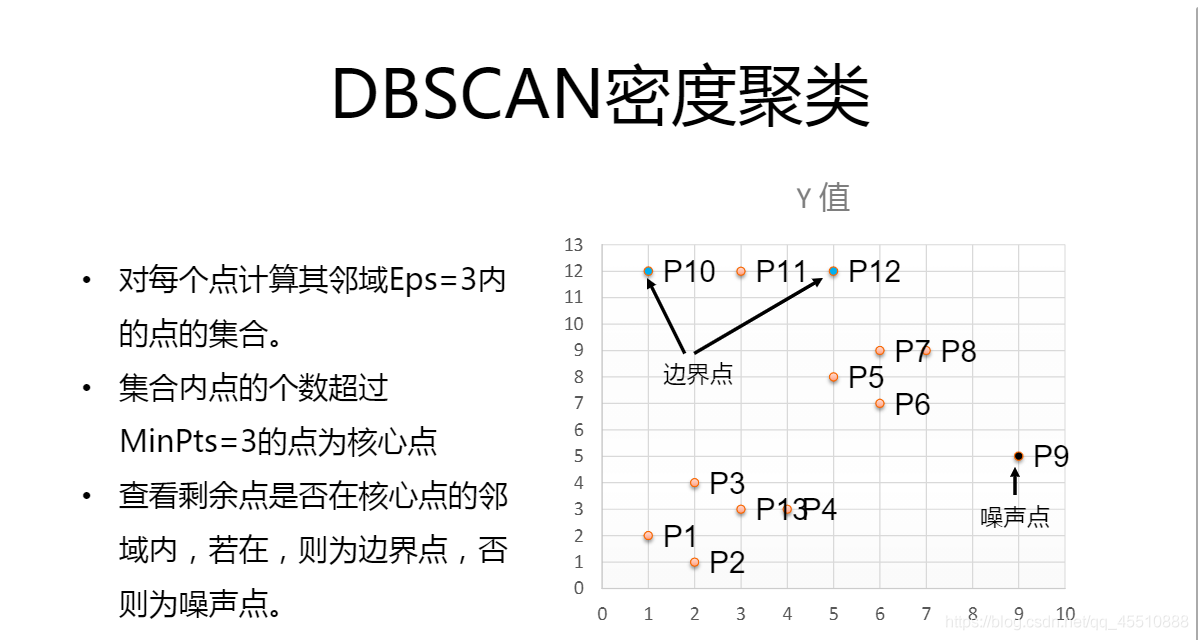
• DBSCAN：基于密度的算法，不需要人为指定簇的个数，故最终簇的个数不确定。将数据点分为3类：
  ——核心点：在给定半径内含有超过确定个数的点，即临近点比较多
  ——边界点：在核心点的邻域内，但不满足核心点的要求
  ——噪音点：不满足以上条件
  流程为将所有点标记为核心点、边界点或者噪音点；删除噪音点；在给定距离内的核心点赋予边；每组连通的核心点形成一个簇；将边界点分配到与其关联的核心点的簇中。

例子：比如目前有全国30个城市的几个方面的数据，例如在衣、食、住、行4个方面的消费，要把30个城市分成几个不同的类别，就要用到聚类算法。

（2）降维（decomposition）：尽可能保证原本数据特征不变的情况下，将高维数据转化为低维数据，一般用作数据的可视化，或者减轻后续计算的数据量。

算法

• PCA：将线性相关的高维变量合成线性无关的低维向量，称为主成分，主成分尽可能保留原始数据的信息。简单来说，矩阵的主成分就是其协方差矩阵对应的特征向量，按照大小，找出前m个（就是我们要降到的低维个数）特征值。

• NMF：非负矩阵分解，原理就是非负矩阵可以分解为两个非负矩阵的乘积。

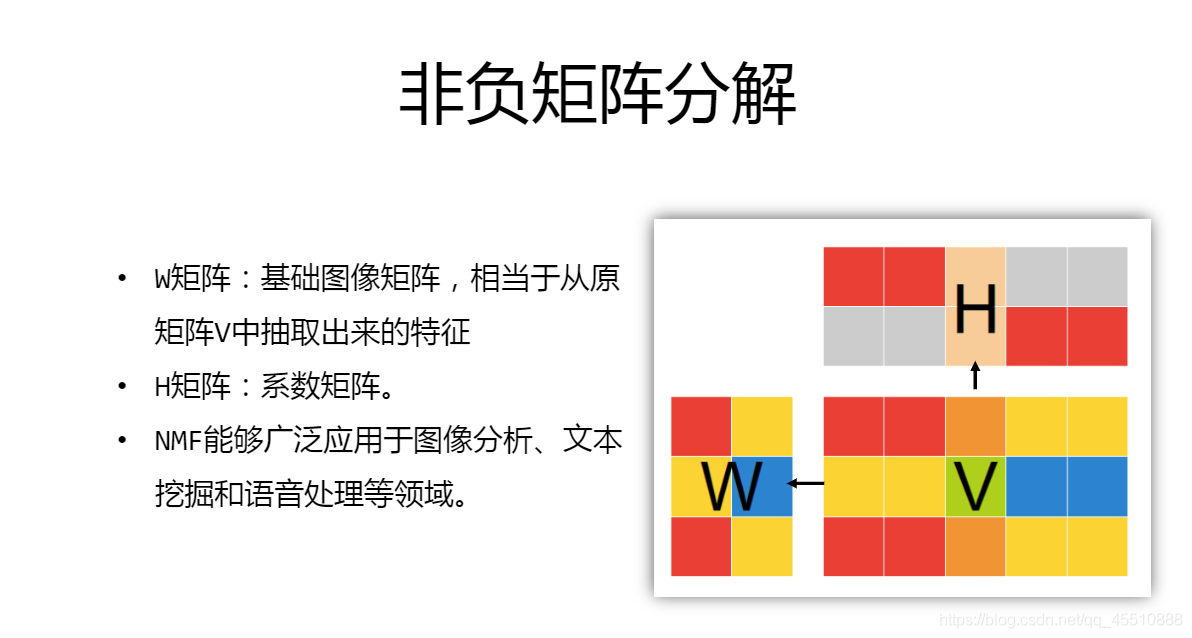
例子：鸢尾花是一个常见的数据集，但是其是4个指标，即4维，无法直接看出其空间分布，于是需要降维将其转化为2维平面上的点，易于观察。

2.监督学习

监督学习即利用有标签的数据，学习其规律，目的是对未知数据进行很好的预测，一般分为分类和回归。监督学习都会有训练集和测试集之分。

（1）分类：输出离散即为分类。根据对训练集的学习，面对测试集可以准确将其分到所属类别，有二分类，也有多分类。

算法

• kNN：通过计算一个数据点与所有数据点之间的距离，根据给定的邻居个数N，取出其邻居各自的类别，它的邻居哪一类最多，就判断此样本点属于哪一类。
  k的取值很关键，较大时虽然会根据更多的样本点来判断，但是也会因为引入距离较远的样本，从而导致预测错误；较小时，容易出现过拟合现象，容易被噪音点影响。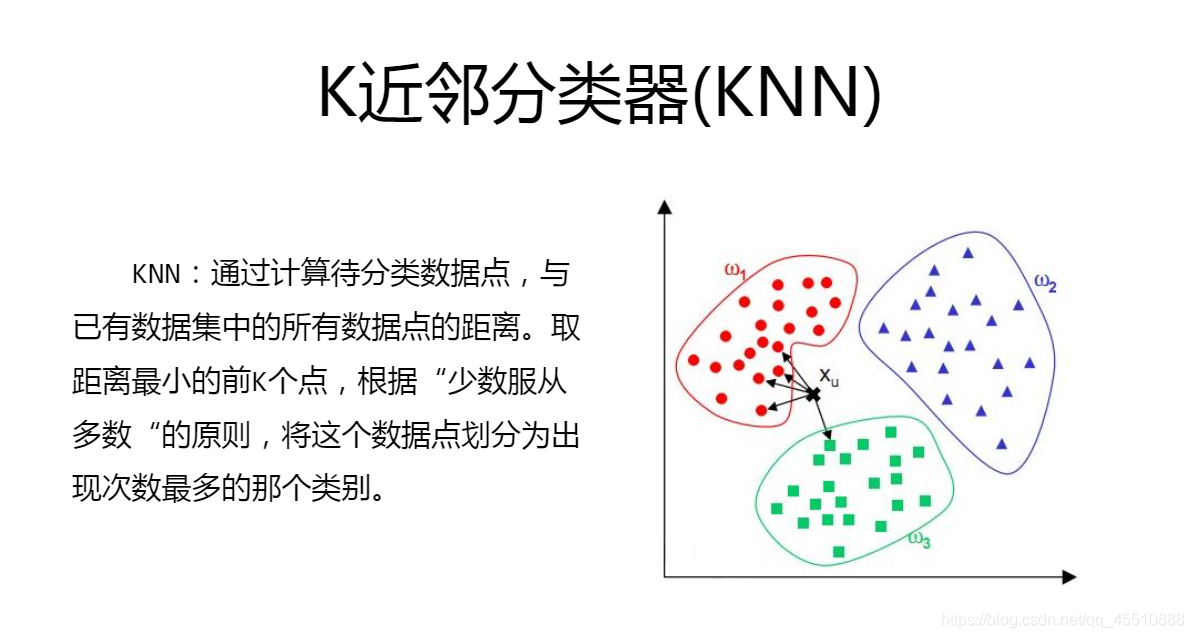
  
• 决策树：西瓜书的第一个模型。通常问题会被诸多因素影响，而我们的目的是产生一个最合适的判断模型，只要顺着树枝就可以得到正确的结果。

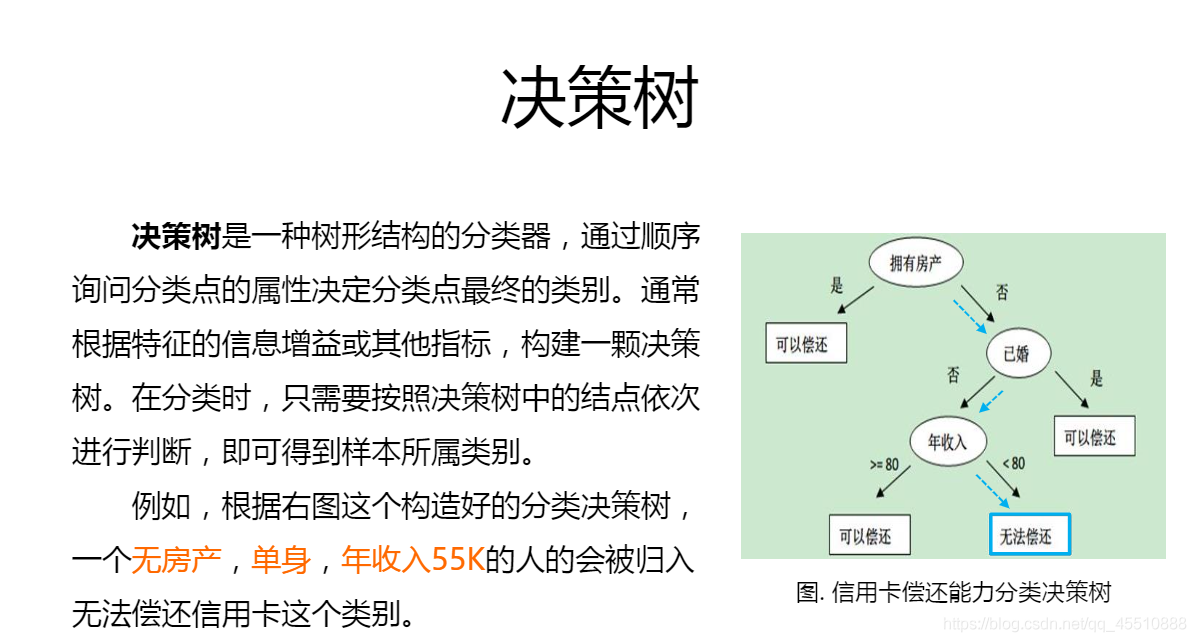
• 朴素贝叶斯：首先概率论中学过贝叶斯定理，朴素贝叶斯就是为了求出后验概率最大的y，作为其分类结果。

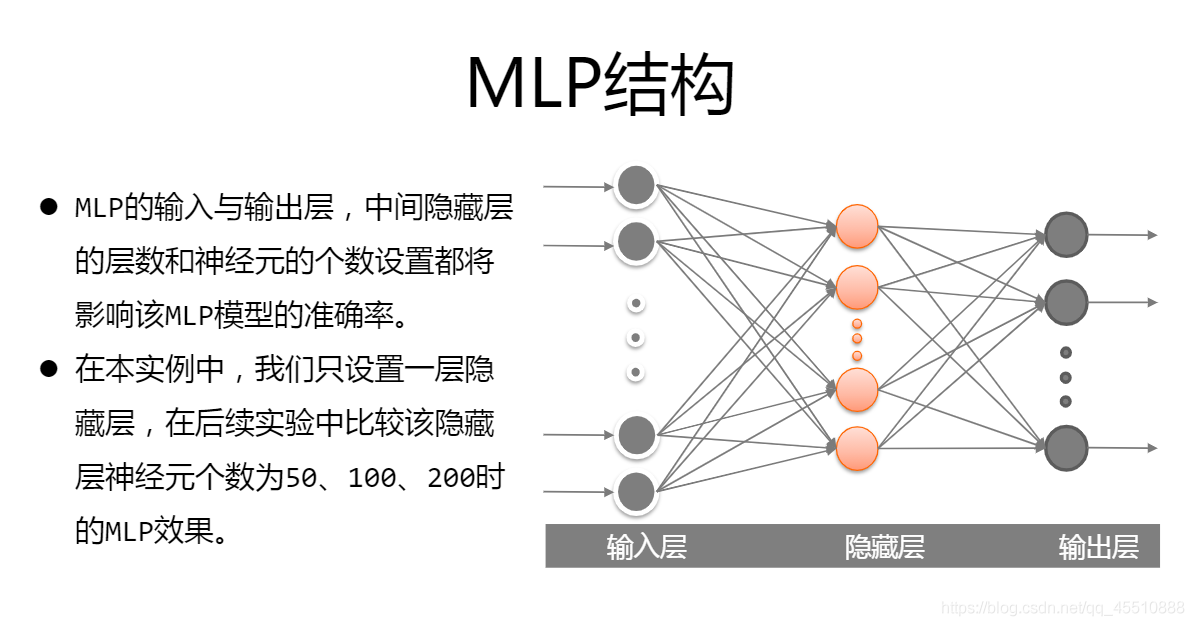
• MLP：即多层感知机。最简单的2层神经网络也叫做感知机，中间加入隐含层后即为多层感知机，是一种很简单的神经网络。

例子：根据对数据集中的猫和狗的学习，从而产生合适的分类器，对未知图片可以判断其是猫还是狗。

（2）回归：输出连续即为回归。与分类类似，只不过是输出为连续的情况，根据训练集去预测，对于输入可以给出一个合适的数值。自变量（特征）只有一个时为一元回归，多个时为多元回归。

算法

• 简单回归
• 多项式回归
• 岭回归：上述二者都是基于最小二乘法进行拟合，岭回归相比较而言是一种改良的最小二乘法。

例子：最简单的回归即为散点图的回归，下图给了一个二维的例子，高维可以类比；回归也可以分为线性和非线性。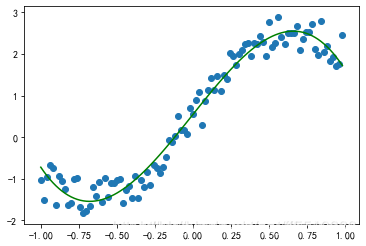

个人看来回归更倾向于预测，例如股票（当然这个很难预测）、交通流量预测，可以理解为就是对时间序列进行拟合，只不过将序列替换为高维的概念。

3.强化学习

强化学习是一种试错学习，通过环境提供的反馈调整策略，最终达到奖赏最大的目的。

算法

• 马尔可夫决策过程MDP：和信息论中的马尔可夫链很像，根据当前状态和转移概率求得下一个状态，是基于模型的算法。
• 蒙特卡洛强化学习：当环境中状态太多时，学习算法不再依赖于环境建模，即为免模型算法。这里提到了贪心策略。

• Q-learning：结合动态规划和蒙特卡洛强化学习。
• 深度强化学习DRL：将深度学习和传统强化学习结合，也避免了状态过多的问题，直接从环境（输入）和动作（输出）去学习。
• DQN：Deep Q Network，DL+Q-learning