JavaScript 沿五角星形线摆动的小圆 JavaScript实现沿五角星形线摆动的小圆实例详解

时间:2021-01-29 aTeacher 人气:0

五角星形线的笛卡尔坐标方程式可设为：

r=10+(3*sin(θ*2.5))^2 

x=r*cos(θ)

y=r*sin(θ) （0≤θ≤2π）

根据这个曲线方程，在[0,2π]区间取一系列角度值，根据给定角度值计算对应的各点坐标，然后在计算出的坐标位置绘制一个填充色交替变换的小圆，从而得到沿五角星形线摆动的小圆的动画效果。

编写如下的HTML代码。

<!DOCTYPE html>

<html>

<head>

<title>沿曲线摆动的小圆</title>

</head>

<body>

<canvas id="myCanvas" width="400" height="400" style="border:3px double #996633;">

</canvas>

<script type="text/javascript">

 var canvas = document.getElementById('myCanvas');

 var context = canvas.getContext('2d');

 var i = 0;

 var j = Math.PI/32;

 var t = 0;

 var col = ['red','orange','yellow','green','cyan','blue','magenta'];

 function loop()

 {

 t = t + 1;

 i = i + j;

 if (t > 6) { t = 0; }

 var r=10+9*Math.sin(2.5*i)*Math.sin(2.5*i);

 var x = 7*r*Math.cos(i)+200;

 var y = 7*r*Math.sin(i)+200;

 context.beginPath();

 context.moveTo(200, 200);

 context.lineTo(x, y);

 context.lineCap = 'round';

 context.strokeStyle = 'rgba(50,100,255,0.6)';

 context.stroke();

 context.beginPath();

 context.moveTo(200, 200);

 context.arc(x, y, 8, 0, 2 * Math.PI);

 context.fillStyle = col[t];

 context.fill();

 if (i>2*Math.PI)

 {

 j =-Math.PI/32;

 context.clearRect(0, 0, 400, 400);

 }

 if (i<0)

 { 

 j = Math.PI/32;

 context.clearRect(0, 0,400, 400);

 }

 }

 setInterval('loop()',300);

</script>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以在浏览器窗口中呈现出如图1所示的沿五角星形线摆动的小圆动画效果。

图1 沿五角星形线摆动的小圆

将上面程序中的语句

var r=10+9*Math.sin(2.5*i)*Math.sin(2.5*i);

var x = 7*r*Math.cos(i)+200;

var y = 7*r*Math.sin(i)+200;

改写为：

 var e=80*(1+Math.cos(2*i)/4);

  var f=e*(1+Math.sin(4*i));

  var x=200+f*Math.cos(i);

  var y=200-f*Math.sin(i);

就可以在画布中看到如图2所示的沿四瓣花型线摆动的小圆。

图2 沿四瓣花型线摆动的小圆

若改写为：

var r = 200 * Math.pow(Math.cos(i/3),3);

 var x = 200 + r * Math.sin(i);

 var y = 110 + r * Math.cos(i);

同时修改 if (i>2*Math.PI) 为 if (i>3*Math.PI)

就可以在画布中看到如图3所示的沿苹果形线摆动的小圆。

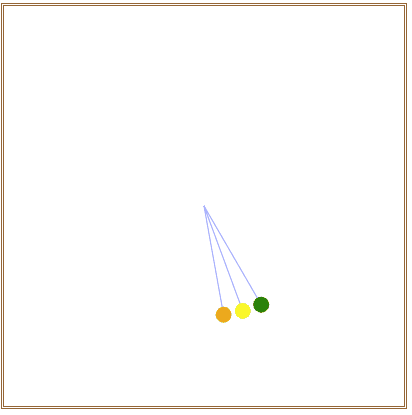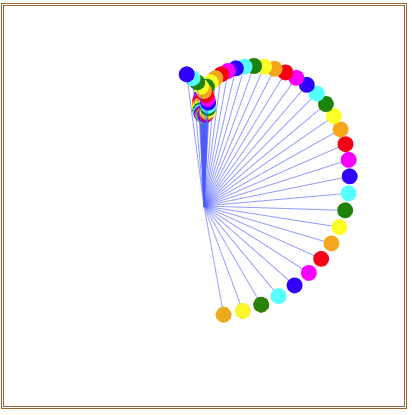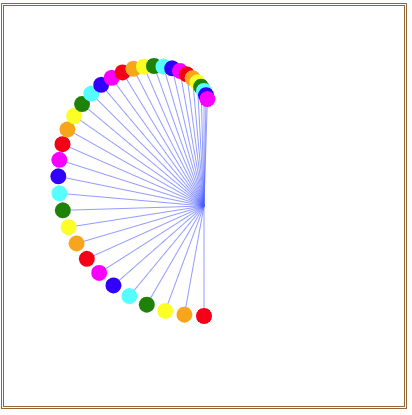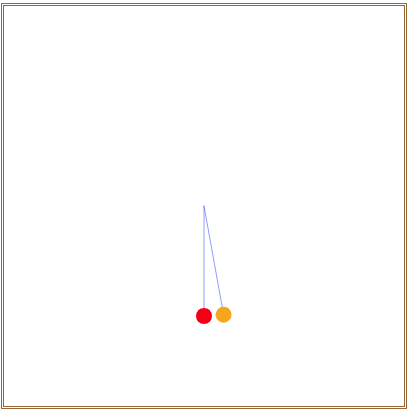
图3 沿苹果形线摆动的小圆

若改写为：

var r=100*Math.pow(Math.cos(2*i),0.5);

var x = 200 + 160*Math.sin(i)*Math.sin(i)*Math.sin(i);

var y = -(-170+ 10*(13*Math.cos(i)- 5*Math.cos(2*i) - 2*Math.cos(3*i) - Math.cos(4*i)));

就可以在画布中看到如图4所示的沿心形线摆动的小圆。

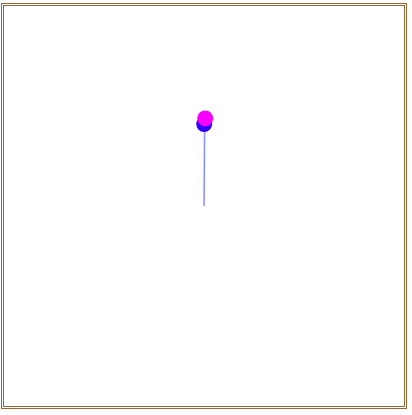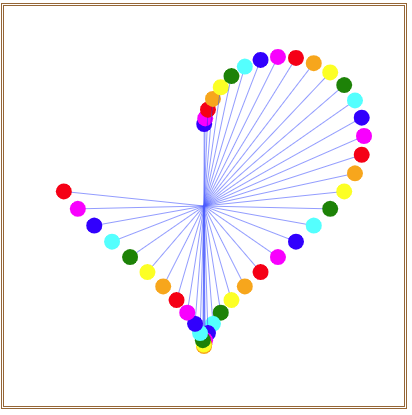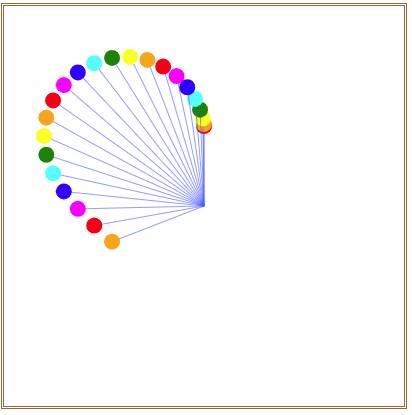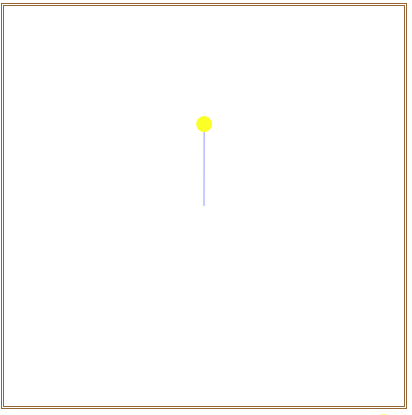
图4 沿心形线摆动的小圆

有兴趣的读者，可以根据自己感兴趣的曲线的参数方程，适当修改坐标位置（x,y）的计算语句，就可以看到沿指定曲线摆动的小圆的动画效果。

加载全部内容