java同态加密算法 java实现同态加密算法的实例代码
向彪-blockchain 人气:0什么是同态加密?
同态加密是上世纪七十年代就被提出的一个开放问题,旨在不暴露数据的情况下完成对数据的处理,关注的是数据处理安全。
想象一下这样一个场景,作为一名满怀理想的楼二代,你每天过着枯燥乏味的收租生活,希望摆脱世俗的枷锁、铜臭的苟且去追求诗与远方。
你需要雇一个代理人去承担收租的粗活,但又不希望其窥探你每月躺赚的收入。于是,你请高人打造了一套装备,既能保证代理人顺利完成收租,又不会泄露收入信息。
这套装备包括信封、胶水、皮夹和神奇剪刀,每一样东西都有奇特的功能:
- 信封一旦用胶水密封,只有神奇剪刀才能拆开。
- 不论信封里装了多少钱,信封的大小和重量都不会发生改变。
- 把多个信封放在皮夹里后,信封会在不拆开的情况下两两合并,最后变成一个信封,里面装的钱正好是合并前所有信封金额的总和。
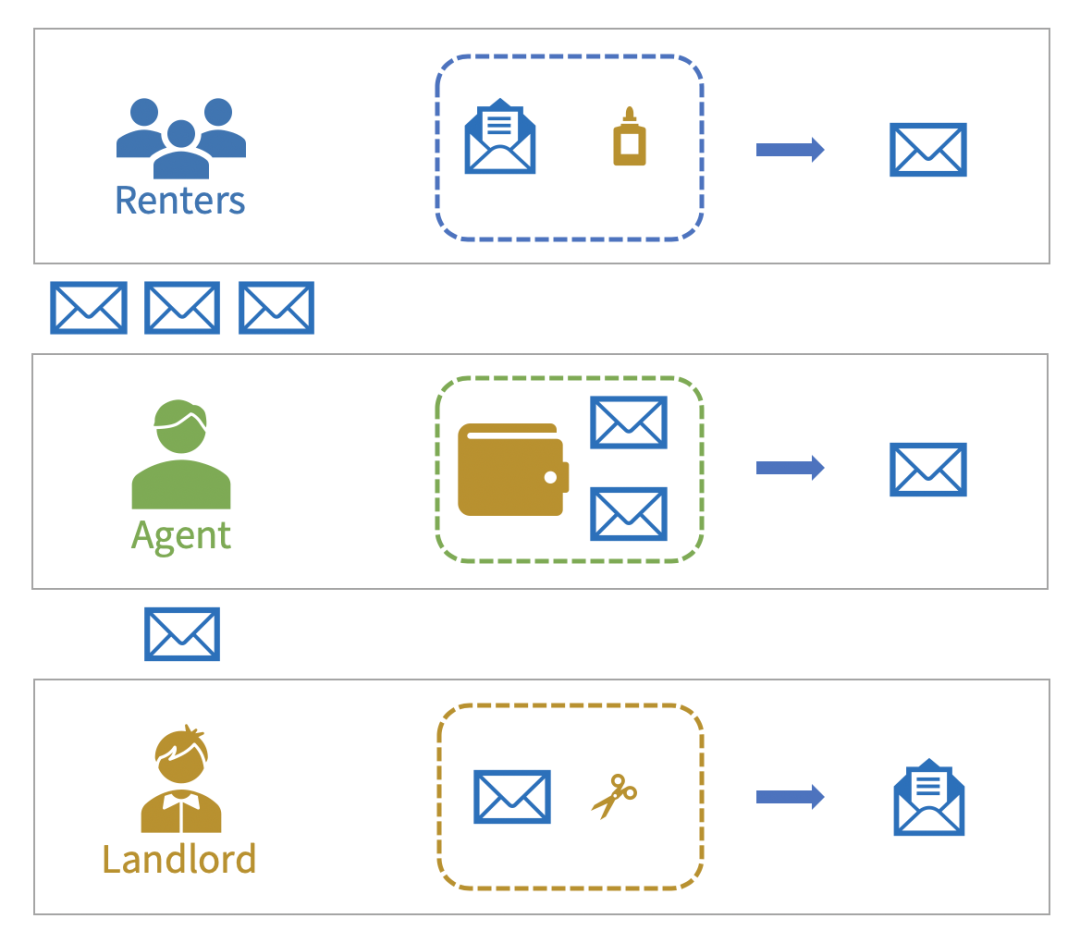
你把信封和胶水分发给所有租客,把皮夹交给代理人。
到了约定交租的日子,租客把租金放到信封里密封后交给代理人;代理人收齐信封,放到皮夹中,最后得到一个装满所有租金的信封,再转交给你;你使用神奇剪刀拆开,拿到租金。
在这个场景中,信封的a、b两个性质其实就是公钥加密的特性,即使用公钥加密得到的密文只有掌握私钥的人能够解密,并且密文不会泄露明文的语义信息;而c则代表加法同态的特性,两个密文可以进行计算,得到的结果解密后正好是两个原始明文的和。
原理:
paillier加密算法步骤:密钥生成、加密、解密
1、密钥生成
1.1 随机选择两个大质数p和q满足gcd(pq,(p-1)(q-1)) =1。这个属性保证两个质数长度相等。
1.2 计算n=pq和λ=lcm(p-1,q-1)
1.3 选择随机整数g(g ∈ Z n 2 ∗ g∈Z_{n^2}^*g∈Zn2∗),使得满足n整除g的阶。
1.4 公钥为(N,g)
1.5 私钥为λ
g c d ( L ( g λ m o d n 2 ) , n ) = 1 gcd(L(g^λ mod n^2),n)=1gcd(L(gλmodn2),n)=1
2、加密
2.1 选择随机数r ∈ Z n r∈Z_nr∈Zn
2.2 计算密文
c = E ( m , r ) = g m r n m o d n 2 , r ∈ Z n c = E(m,r) = g^m r^n mod n^2 ,r∈Z_nc=E(m,r)=gmrnmodn2,r∈Zn,其中m为加密信息。
3、解密
m = D ( c , λ ) = ( L ( c λ m o d n 2 ) / L ( g λ m o d n 2 ) ) m o d n , 其 中 L ( u ) = u − 1 / N m= D(c,λ)=(L(c^λ mod n^2)/L(g^λ mod n^2)) mod n,其中 L(u)=u-1/Nm=D(c,λ)=(L(cλmodn2)/L(gλmodn2))modn,其中L(u)=u−1/N
java实现:
package com;
/**
* This program is free software: you can redistribute it and/or modify it
* under the terms of the GNU General Public License as published by the Free
* Software Foundation, either version 3 of the License, or (at your option)
* any later version.
*
* This program is distributed in the hope that it will be useful, but WITHOUT
* ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or
* FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for
* more details.
*
* You should have received a copy of the GNU General Public License along with
* this program. If not, see <http://www.gnu.org/licenses/>.
*/
import java.math.*;
import java.util.*;
/**
* Paillier Cryptosystem <br>
* <br>
* References: <br>
* [1] Pascal Paillier,
* "Public-Key Cryptosystems Based on Composite Degree Residuosity Classes,"
* EUROCRYPT'99. URL:
* <a href="http://www.gemplus.com/smart/rd/publications/pdf/Pai99pai.pdf" rel="external nofollow" >http:
* //www.gemplus.com/smart/rd/publications/pdf/Pai99pai.pdf</a><br>
*
* [2] Paillier cryptosystem from Wikipedia. URL:
* <a href="http://en.wikipedia.org/wiki/Paillier_cryptosystem" rel="external nofollow" >http://en.
* wikipedia.org/wiki/Paillier_cryptosystem</a>
*
* @author Kun Liu (kunliu1@cs.umbc.edu)
* @version 1.0
*/
public class Paillier {
/**
* p and q are two large primes. lambda = lcm(p-1, q-1) =
* (p-1)*(q-1)/gcd(p-1, q-1).
*/
private BigInteger p, q, lambda;
/**
* n = p*q, where p and q are two large primes.
*/
public BigInteger n;
/**
* nsquare = n*n
*/
public BigInteger nsquare;
/**
* a random integer in Z*_{n^2} where gcd (L(g^lambda mod n^2), n) = 1.
*/
private BigInteger g;
/**
* number of bits of modulus
*/
private int bitLength;
/**
* Constructs an instance of the Paillier cryptosystem.
*
* @param bitLengthVal
* number of bits of modulus
* @param certainty
* The probability that the new BigInteger represents a prime
* number will exceed (1 - 2^(-certainty)). The execution time of
* this constructor is proportional to the value of this
* parameter.
*/
public Paillier(int bitLengthVal, int certainty) {
KeyGeneration(bitLengthVal, certainty);
}
/**
* Constructs an instance of the Paillier cryptosystem with 512 bits of
* modulus and at least 1-2^(-64) certainty of primes generation.
*/
public Paillier() {
KeyGeneration(512, 64);
}
/**
* Sets up the public key and private key.
*
* @param bitLengthVal
* number of bits of modulus.
* @param certainty
* The probability that the new BigInteger represents a prime
* number will exceed (1 - 2^(-certainty)). The execution time of
* this constructor is proportional to the value of this
* parameter.
*/
public void KeyGeneration(int bitLengthVal, int certainty) {
bitLength = bitLengthVal;
/*
* Constructs two randomly generated positive BigIntegers that are
* probably prime, with the specified bitLength and certainty.
*/
p = new BigInteger(bitLength / 2, certainty, new Random());
q = new BigInteger(bitLength / 2, certainty, new Random());
n = p.multiply(q);
nsquare = n.multiply(n);
g = new BigInteger("2");
lambda = p.subtract(BigInteger.ONE).multiply(q.subtract(BigInteger.ONE))
.divide(p.subtract(BigInteger.ONE).gcd(q.subtract(BigInteger.ONE)));
/* check whether g is good. */
if (g.modPow(lambda, nsquare).subtract(BigInteger.ONE).divide(n).gcd(n).intValue() != 1) {
System.out.println("g is not good. Choose g again.");
System.exit(1);
}
}
/**
* Encrypts plaintext m. ciphertext c = g^m * r^n mod n^2. This function
* explicitly requires random input r to help with encryption.
*
* @param m
* plaintext as a BigInteger
* @param r
* random plaintext to help with encryption
* @return ciphertext as a BigInteger
*/
public BigInteger Encryption(BigInteger m, BigInteger r) {
return g.modPow(m, nsquare).multiply(r.modPow(n, nsquare)).mod(nsquare);
}
/**
* Encrypts plaintext m. ciphertext c = g^m * r^n mod n^2. This function
* automatically generates random input r (to help with encryption).
*
* @param m
* plaintext as a BigInteger
* @return ciphertext as a BigInteger
*/
public BigInteger Encryption(BigInteger m) {
BigInteger r = new BigInteger(bitLength, new Random());
return g.modPow(m, nsquare).multiply(r.modPow(n, nsquare)).mod(nsquare);
}
/**
* Decrypts ciphertext c. plaintext m = L(c^lambda mod n^2) * u mod n, where
* u = (L(g^lambda mod n^2))^(-1) mod n.
*
* @param c
* ciphertext as a BigInteger
* @return plaintext as a BigInteger
*/
public BigInteger Decryption(BigInteger c) {
BigInteger u = g.modPow(lambda, nsquare).subtract(BigInteger.ONE).divide(n).modInverse(n);
return c.modPow(lambda, nsquare).subtract(BigInteger.ONE).divide(n).multiply(u).mod(n);
}
/**
* sum of (cipher) em1 and em2
*
* @param em1
* @param em2
* @return
*/
public BigInteger cipher_add(BigInteger em1, BigInteger em2) {
return em1.multiply(em2).mod(nsquare);
}
/**
* main function
*
* @param str
* intput string
*/
public static void main(String[] str) {
/* instantiating an object of Paillier cryptosystem */
Paillier paillier = new Paillier();
/* instantiating two plaintext msgs */
BigInteger m1 = new BigInteger("20");
BigInteger m2 = new BigInteger("60");
/* encryption */
BigInteger em1 = paillier.Encryption(m1);
BigInteger em2 = paillier.Encryption(m2);
/* printout encrypted text */
System.out.println(em1);
System.out.println(em2);
/* printout decrypted text */
System.out.println(paillier.Decryption(em1).toString());
System.out.println(paillier.Decryption(em2).toString());
/*
* test homomorphic properties -> D(E(m1)*E(m2) mod n^2) = (m1 + m2) mod
* n
*/
// m1+m2,求明文数值的和
BigInteger sum_m1m2 = m1.add(m2).mod(paillier.n);
System.out.println("original sum: " + sum_m1m2.toString());
// em1+em2,求密文数值的乘
BigInteger product_em1em2 = em1.multiply(em2).mod(paillier.nsquare);
System.out.println("encrypted sum: " + product_em1em2.toString());
System.out.println("decrypted sum: " + paillier.Decryption(product_em1em2).toString());
/* test homomorphic properties -> D(E(m1)^m2 mod n^2) = (m1*m2) mod n */
// m1*m2,求明文数值的乘
BigInteger prod_m1m2 = m1.multiply(m2).mod(paillier.n);
System.out.println("original product: " + prod_m1m2.toString());
// em1的m2次方,再mod paillier.nsquare
BigInteger expo_em1m2 = em1.modPow(m2, paillier.nsquare);
System.out.println("encrypted product: " + expo_em1m2.toString());
System.out.println("decrypted product: " + paillier.Decryption(expo_em1m2).toString());
//sum test
System.out.println("--------------------------------");
Paillier p = new Paillier();
BigInteger t1 = new BigInteger("21");System.out.println(t1.toString());
BigInteger t2 = new BigInteger("50");System.out.println(t2.toString());
BigInteger t3 = new BigInteger("50");System.out.println(t3.toString());
BigInteger et1 = p.Encryption(t1);System.out.println(et1.toString());
BigInteger et2 = p.Encryption(t2);System.out.println(et2.toString());
BigInteger et3 = p.Encryption(t3);System.out.println(et3.toString());
BigInteger sum = new BigInteger("1");
sum = p.cipher_add(sum, et1);
sum = p.cipher_add(sum, et2);
sum = p.cipher_add(sum, et3);
System.out.println("sum: "+sum.toString());
System.out.println("decrypted sum: "+p.Decryption(sum).toString());
System.out.println("--------------------------------");
}
}
参考:https://mp.weixin.qq.com/s?__biz=MzA3MTI5Njg4Mw==&mid=2247486135&idx=1&sn=8c9431012aef19bbdefdcd673a783c34&chksm=9f2ef8aba85971bdfb623e8303b103fd70ac2a5ad802668388233ca930d1b0cd77fb02d4b0f2&scene=21#wechat_redirect
https://www.csee.umbc.edu/~kunliu1/research/Paillier.html
总结
加载全部内容