斯坦福算法分析和设计_2. 排序算法MergeSort

 

Motivate

MergeSort是个相对古老的算法了，为什么现在我们还要讨论这么古老的东西呢？有几个原因:

题目

 

输入一个数组，数组里面的每个数字是不重复的，输出是已经排序好的数组。

比如输入的是:

期望输出的是:

可能之前我们有所知道一些排序算法，比如SelectionSort，扫描全数组找到最小元素，把它放到输出数组的第一位，接着扫描复制次小的元素，以此类推；比如BubbleSort，对相邻无序的元素进行比较，执行反复的交换，直到最后数组完成排序。等等。但这些算法的问题就是运行时间是平方级的。那我们来看看今天这个排序算法用更少的运行时间是怎么实现的。

例子 想要理解MergeSort算法是如何运行的，一个最简单的方法就是看看具体的例子。

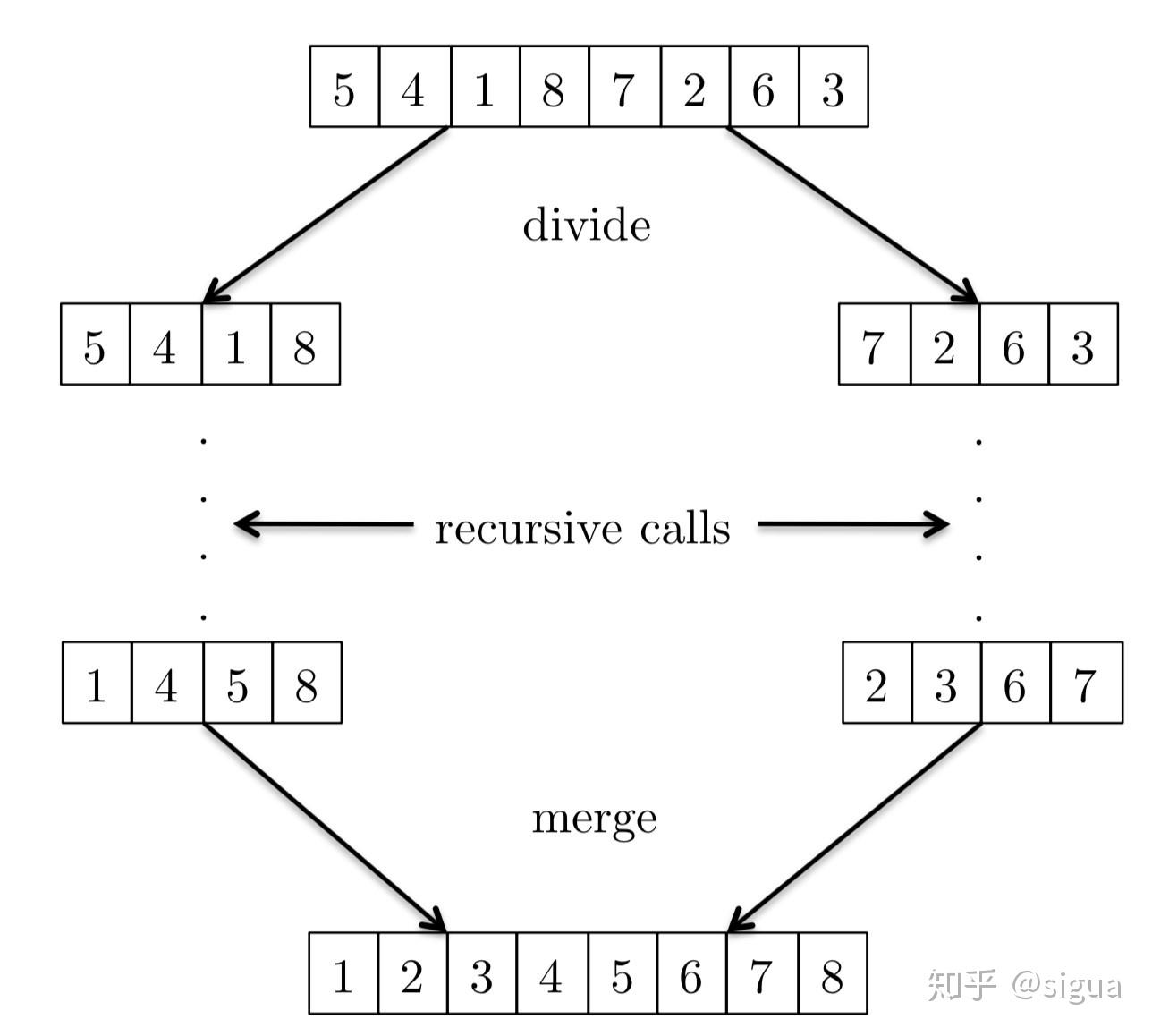
整体过程就是:

它把数组 [5, ,4, 1, 8, 7, 2, 6, 3] 划分为更小的数组(子问题)[5, 4, 1, 8] 和 [7, 2, 6, 3]排序，通过神奇的递归操作，得到每个排序后的子数组，再将子数组合并起来。

伪代码 将上面的图换成伪代码就是这样的过程

而这个Merge程序怎么实现呢？

由上面的图我们可以知道，Merge的时候，其实输入两个已经排序好的数组C, D，再把它们排序输出到B。

索引 k 操控的是输出数组，索引 i，j 操控的是已排序好的C和D子数组，都是从左向右扫描。每一次的for循环，其实就是找C和D中最小的数字，因为C和D是已排序好的数组，所以最小的数字就是i或j对应的元素。比较后把它放入输出数组B中，并将对应的索引+1，这样下次循环就跳过已复制的元素了。所以最后的数组B输出是按序方式生成的。

算法分析

我们先来对Merge程序算算它的执行操作数量。 第1，2行有一次赋值操作。 第3行是一个for循环，每一个for循环里，有比较操作(C[i]和D(i)比较)，赋值操作(B[k]的赋值)，递增操作(i或j加1)，循环变量k还要加1，所以每一次循环一共有4次操作。

一共就是4n+2次操作，为了后面的计算方便，当n>=1时，4n+2<6n(去掉常数项), 我们取6n次操作作为Merge程序操作上界。

我们现在再来看MergeSort的运行时间。 为了简单起见，假如输入数组的长度是n的2次方(如果没有这个假设只需要额外工作就能消除这个假设)，我们用递归树的方法来分析运行时间的上界，每一个节点就表示一次递归调用。

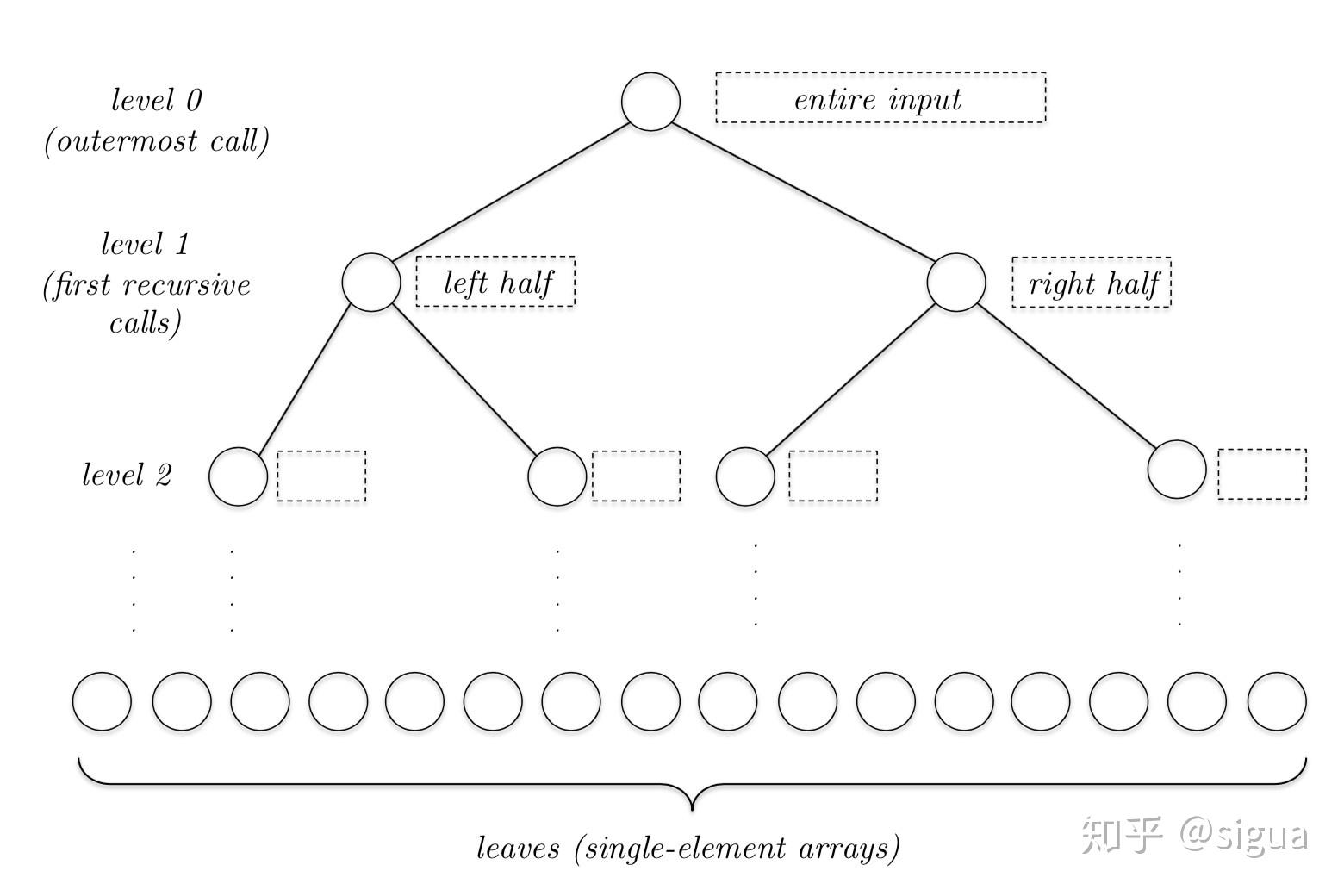
最外层是整个原始的输入数组，它在进行MergeSort的时候会有2个递归调用，所以这是一个二叉树(每个节点都有两个子节点)，第一层的2个节点就是原始数组的左半部分和右半部分，再次递归最后到达最底层，一个长度为1或0的数组。我们需要知道几个数量:

原始数组长度是n，递归树有多少层？

由于每深入一层，数组长度就缩小一半，第0层是n，第1层是n/2(除了一次2)，第2层是n/4(除了2次2)，最后一层的数组长度是不大于1的，就是除以了log2(n)次2，所以最后一层是log2(n)层。（也可以假定n/2^a = 1, 求解a）如果没有n是2的次方这个假设，就向上取整。一共就是log2(n) +1层。

递归树的第j层有多少个节点(子问题)？每个节点的数组长度是多少？

因为每一层的递归数量是前一层的两倍，所以第j层就有2^j个子问题。每个节点的长度，总长度是n，均分到每个节点就是n/(2^j)个长度。

所以总的运行时间就是：

层数 * 每一层的工作量

= 层数 * (第 j 层的子问题数量 * 每个第j层子问题完成的工作数) = 层数 * (第 j 层的子问题数量 * (每个第j层子问题的规模 * Merge的时间))

= (log2(n)+1) * ( 2^j * n/(2^j) * 6n)

=6n * log2(n) +6n

= O(nlogx(n))

这时候，我们就可以理直气壮的说递归的分治算法比其它更简单的算法要快的多啦。看图直观感受一下

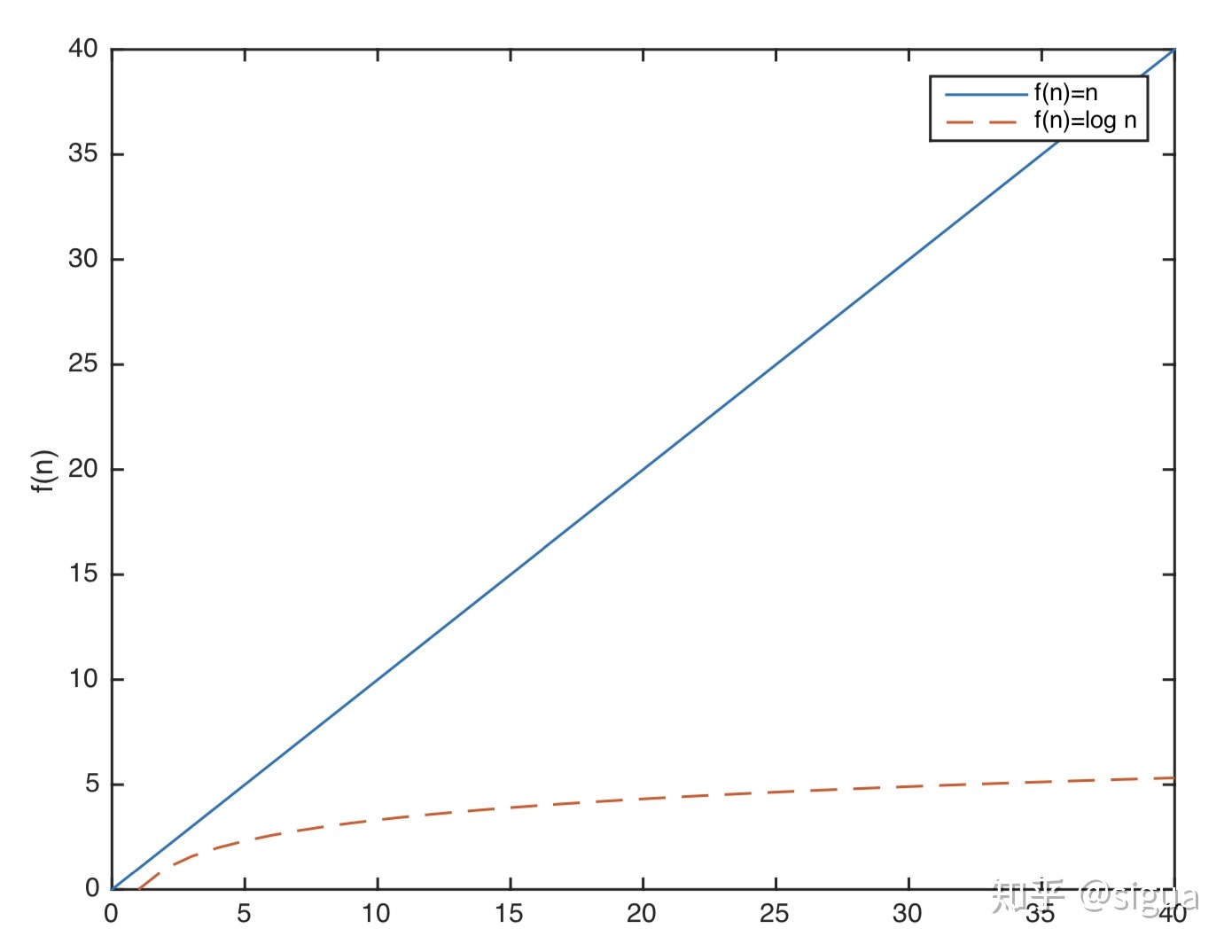
当数据非常大的时候，它是非常有优势的，指数函数增长十分的缓慢。

今日互动

有什么不明白的欢迎在评论区留言。