深度学习论文翻译解析(七):Support Vector Method for Novelty Detection
战争热诚 人气:4论文标题:Support Vector Method for Novelty Detection
论文作者:Bernhard Scholkopf, Robert Williamson, Alex Smola .....
论文地址:http://papers.nips.cc/paper/1723-support-vector-method-for-novelty-detection.pdf
声明:小编翻译论文仅为学习,如有侵权请联系小编删除博文,谢谢!
小编是一个机器学习初学者,打算认真学习论文,但是英文水平有限,所以论文翻译中用到了Google,并自己逐句检查过,但还是会有显得晦涩的地方,如有语法/专业名词翻译错误,还请见谅,并欢迎及时指出。

摘要
假设给你一个从基本概率分布P中提取的数据集,你想估计一个输入空间的“简单”子集,这样从 P中提取的测试点位于S 之外的概率等于和之间指定的某个先验概率。我们提出了一种方法来解决这个问题,尝试估计一个函数 f ,它在S上是正的,在补语上是负的。f的函数形式是根据训练数据的一个潜在的小子集通过核展开给出的;它是通过控制相关特征空间中权重向量的长度来正则化的。我们对算法的统计性能进行了理论分析。该算法是支持向量算法对未标记数据的自然扩展。


1,介绍
近年来,一套新的监督学习核心技术被开发出来[8]。特别是用于模式识别,回归估计和反问题求解的支持向量(SV)算法受到了广泛的关注。有几次尝试将利用核函数计算特征空间内积的思想转移到无监督学习领域。然而,该领域中的问题没有那么明确。一般来说,他们可以被描述为数据的估计函数,这些函数告诉您关于底层分布的一些有趣的信息。例如,核主成分分析可以被描述为对训练数据产生单位方差输出而在特征空间具有最小范数的计算函数[4]。另一种基于核的无监督学习技术,正则化主流形[6],其计算函数可以映射到低维流行上,从而最大程度地减少了正则化量化误差。聚类算法是可以被内核化的无监督学习技术的进一步示例。
一个极端的观点是,无监督学习是关于估计密度的,显然,对于P的密度的了解将使我们能够解决根据数据可以解决的任何问题,本工作解决了一个更简单的问题:提出了一种算法,该算法计算一个二进制函数,该函数应捕获概率密度存在的输入空间中的区域(它的支持),即使大多数数据都位于该区域中的函数 函数为非零[5]。这样做,是符合瓦普尼克(Vapnik)的原则,永远不解决比我们实际需要解决的问题更普遍的问题。此外,它也适用于数据分布密度甚至没有很好定义的情况,例如,如果存在奇异成分,本研究的主要动机是论文[1],事实证明,之前的工作量很大。

2,算法
我们首先介绍术语和符号惯例,我们考虑训练数据 x1, x2....xl 属于 X ,其中 l 属于N 是观测的数量,X是一些集合。为了简单起见,我们将其设为 RN 的一个紧凑子集。设 Φ 是 X -> F 的特性映射,即到点积空间F中的映射,使得Φ 的图像点积可以通过评估一些简单的核来计算
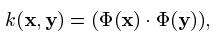
例如高斯核:
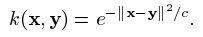
索引 i 和 j 被认为在 i,....,j 的范围内(简写为:i, j 属于 [l])粗体的希腊字母表示 l-维向量,其分量用普通字体标注。
在本节的其余部分中,我们将开发一种算法,该算法返回一个函数F,该函数在捕获大部分数据点的“小”区域中取值 +1,而在其他地方则取值 -1。我们的策略是将数据映射到与内核相对应的特征空间中,并以最大的余量将他们与原点分开。对于新点 x,值f(x) 是通过评估特征空间上落在超平面的哪一侧来确定。通过自由利用不同类型的核函数,此简单的几何图像对应于输入空间中的各种非线性估计。
该问题的优化目标与二分类 SVM 略微不同,但依然很相似。

为了将数据集与原点分离,我们求解一下二次规划:

此处,v属于(0, 1) 是一个参数,其含义稍后将变得清楚。由于非零松弛变量 ξi 在目标函数中受到惩罚,我们可以预期,如果 w 和 p解决了这个问题,则对于训练集中包含的大多数示例 xi ,决策函数 f(x) = sgn((w*Φ(x))-p) 将会为正,而SV类型正则项 W 仍然很小。这两个目标之间的实际权衡由 v 控制的。导出对偶问题,并使用(1),可以证明该解决方案具有 SV 展开。
注意,这里的 v 类似于二分类 SVM 中的C,同时:
- 1, v 为异常值的分数设置了一个上限(训练数据集里面被认为是异常的)
- 2, v 是训练数据集里面做为支持向量的样例数量的下届
因为这个参数的重要性,这种方法也被称为 v-SVM 。采用 Lagrange技术并且采用 dotproduct calculation,确定函数如下:
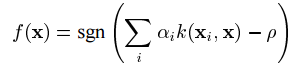
具有非零 i 的模式 Xi 称为SV,其中找到系数作为对偶问题的解:


可以使用标注QP例程解决此问题。然而,它确实拥有一些特性,使其与一般 qp 不同,最显著的时约束的简单性。可以通过应用为此目的开发的 SMO 变体加以利用[3]。
偏移量p可以通过利用对于不在上限或下限的任何 αi 的对应模式 xi 满足 ρ = (w*Φ(x))=。。。
注意,如果 v 接近,Lagrange 乘子的上界区域无穷大,即(6)中的第二个不等式约束变为无效。从原始目标函数(3)可以看出,由于错误的惩罚变得无限,因此,这个问题类似于相应的硬边界算法,可以证明如果数据集与原点可分离,则该算法将找到具有唯一属性的支持超平面,并且在所有此类超平面中,距原点的距离最大[3]。另一方面,如果 v 接近1,则仅约束允许一个解,即所有 i 都在上限 1/(vl) 处。在这种情况下,对于具有整数1 的内核,例如(2)的规范化版本,决策函数对应于阈值 Parzen 窗口估计器。
作为本节的总结,我们注意到,人们还可以使用球来描述特征空间的数据,其实质与【2】的算法(具有硬边界)和【7】的算法(具有软边界)密切相关。对于某些类的核,例如高斯RBF核,可以显示出相应的算法与上面的算法是等价的【3】。

3,理论
在这一节中,我们证明了参数表征了SVs和离群值的分数(命题1)。然后,我们给出了软边值(命题2)和误差界(命题5)的鲁棒性结果。进一步的结果和证明已在本论文中的全文中报告【3】。我们将使用斜体字母表示输入空间中对应模式的特征空间图形,即 xi: = Φ(Xi)。
命题1 假设(4)的解满足 p!=0,以下陈述成立:
(1)是离群值部分的上限
(2)是SVs分数的下限
(3)假设数据是独立与不包含离群分量的分布 P(x) 生成的。此外,假设内核是分析性的并且是非恒定的。渐进的,概率为1,等于SV的分数和异常值的分数。
证明基于对偶问题的约数,适用了离群值必须在上限处具有拉格朗日乘数的事实。
命题2 与W平行的离群值的局部运动不会改变超平面。
我们现在继续讨论一般化的问题。我们的目标是将从相同的基本分布中提取新点位于估计区域之外的概率限制在一定的范围内。我们首先介绍一个通用工具,用于测量映射X到R的F类函数的容量。

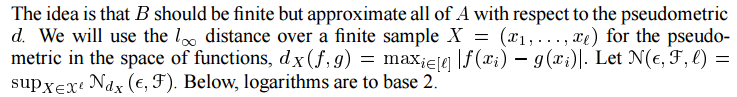
命题3 设(X,d)为伪度量空间,令A为X的子集且epsilon>0。如果每个a属于A,都存在b属于B,使得d(a, b)<=epsilon,A的 epsilon-conver Nd(epsilon, A) 是A的epsilon-cover 的最小基数(如果没有这样的有限覆盖,则定义为无穷大)
这个想法是B应该是有限的,但相对于伪度量 d 近似于A的全部。我们将在有限空间样本 X=(X1...Xl) 上的 L无穷 距离用于函数空间中的伪度量。 下面的对数以2为底。

命题4 考虑到任何P在X的分布,和任何 rho 属于R,假设x1,....xl 是来自P的i.i.d,然而,如果我们发现 f属于F使得对于所有的 f(xi) = -theta + rho

我们现在考虑对于少数点 f(xi)不能超过 a+b 的可能性,这相当于在算法中具有一个非零的松弛变量 epsilon i ,在定理的应用中,我们取 gama + theta=rho/||W|| 并使用特征空间中的线性函数类,覆盖此类的日志有众所周知的界限。令f 为空间 X 上的实值函数。在theta 属于R,x 属于 X,定义
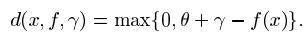
类似的,对于一个训练序列 X,我们定义


命题5 令 theta=R,考虑一个固定但未知的概率分布P在输入空间 X 和范围为[a, b]的一类实数函数F。然后 对于所有的随机绘制的在大小为 l 的训练序列 x,对于所有的 tho>0 并且任何的 f 属于 F,有:

该定理限制了一个新点落入 f(x)的值小于 rho-gamma,这是对分配支持的估计的补充。对的选择在边界所保持的区域的大小(r增加,区域的大小)与它所保持的概率的大小(r 增加,对数覆盖数的大小)之间进行权衡。
结果表明,我们可以用涉及对数覆盖数之比(可以由与 r 成比例的脂肪破碎位数来界定)与训练次数之比的数量来限制点落在估计支持范围之外的概率。示例,再加上涉及松弛变量1范数的因子。它比【1】给出的相关结果更强,因为他们的边界涉及Pollard维数(r趋于0时的脂肪破碎位数)与训练样本数之比的平凡根。


输出的算法描述在Sec.2,是一个函数 f(x) 在示例 xi上大于或等于i。尽管在输入控件中是非线性的,但是这函数实际上在内核k 定义的特征空间中是线性的。同时,权向量的2范数的权限向量是B给出的。因此我们可以将定理应用到函数类F为空间特征中以B为边界的2范数的那些线性函数。如果我们假设 theta是已知的,然后 gamma=rho-theta,因此分布的集合是支持集合的。并且根据函数类别F的对数覆盖范围和松弛变量 ξi 的总和,边界给出了随机生成的点落在该集合之外的可能性,由于F级的对数覆盖数可以由 O限制,因此就权重向量的2范数给出了一个限制。由于日志覆盖数在 类F 的 gamma/2 可以在 O 给出的范围内,这给出了权向量的2范数的界。
理想情况下,人们希望在确定 theta 的值后选择 tho,也许将其作为该值的固定分数。这可以通过在某个可能值的 rho 或至少一个网格的可能值上将结果风险最小化的另一个级别来实现。该结果超出了当前初步论文的范围,但是结果的形式类似于定理5,具有更大的常数和对数因子。
虽然给出具体的理论建议以供实际使用尚未过早,但从上述界限可以清楚地看出一件事。为了归纳为异常的数据,要使用的决策函数应该采用 阈值 eta*rho,其中 eta<1( rho 对应一个非零值)
4,实验
我们将该方法应用于人工数据和真实数据,图1展示了二维玩具示例,并显示了参数设置如何影响解决方案。
接下来,我们描述了对于 USPS 手写数字数据集的实验。该数据库包含大小Wie 16*16=256 的9298 位数字图像;最后的2007年构成测试集。我们在测试集上使用宽度 c = 0.5*256(该数据集上SVM分类器的通用值,参见【2】)的高斯核训练了该算法,并用它来识别离群值——是社区中的民间传说,由于分割错误或标签错误,USPS测试集包含许多难以分类或无法分类的模式。在实验中,我们将输入模式增加了十个与数字的类别标签相对应的维度。这样做的理由是,如果我们忽略标签,就没有希望将错误标签的模式识别为异常值。图2显示了USPS测试集的20个最差离群值。注意,该算法确实提取出很难分配给他们各自类别的模式。在实验中,在以 450 MHz 运行的 Pentium || 上花费了几秒钟,我们使用了 5% 的 v 值。

图1,前两张图片,适用于两个玩具问题的单类SVM;v=c=0.5,域:[-1, 1]2,请注意,在这两种情况下,所有示例中至少 v 的一小部分如何位于估计区域中(参见表)。v的较大的值导致左上角的其他数据点对决策功能几乎没有影响。对于较小的v值,例如 0.1(第三张图片),这些点将不再被忽略。或者,可以通过更改内核宽度(2)来强制算法将这些“离群值”考虑在内:在第四张图片中,使用 c=0.1,v=0.5 可以在不同的长度范围内有效的分析数据,这导致算法考虑了离群值是有意义的点。

图2:由提出的算法识别的离群值,按SVM的负输出(决策函数中 sgn的自变量)排名。输出(为了方便起见,以 10**-5为单位)以斜体写在每个图像的下方,(对应的 )类标签以粗体显示。请注意,大多数示例都是“困难”的,因为他们不是典型的,甚至标记错误的。

5,讨论
可以将当前的工作视为提供一种符合 Vapnik 原理的算法的尝试,该算法永远不会解决比实际感兴趣的问题更笼统的问题。例如,在仅对检测感兴趣的情况下 异常,并不一定总是需要顾及数据的完整密度模型。的确,在几个方面,密度估算比我们所做的更加困难。
从数学上讲,仅当基础概率测度具有绝对连续的分布函数时,密度才会存在。估计大类集合的度量的一般问题(例如,以Borel的意义衡量的集合)是无法解决的(有关讨论,请参见【8】)。因此,我们需要限制自己对某些集合的度量进行陈述。给定一类集合,完成此任务的最简单估计器是经验测度,它只是查看有多少训练点落入感兴趣区域。我们的算法则相反,它从应该落入该区域的的训练点数量开始,然后估计具有所需熟悉的区域。通常,会有很多这样的区域解方案通过应该正则化器才能变得唯一,在我们的情况下,这强制了该区域在与内核关联的特征空间中较小。当然,这意味着,在这种意义上,较小程度的度量取决于所使用的内核,其方式与在特征空间中进行正则化的任何其他方式没有什么不同。但是,在输入空间中进行密度估计时,已经出现了类似的问题。令 P 表示 X 上的密度。如果我们在输入域 X 中执行(非线性)坐标变换,则密度值将发生变化;粗略地说,保持不变的是 px*dx,而 dx 也进行了转换。当直接估计区域的概率度量时,我们不会遇到这个问题,因为区域会相应的自动更改。
我们选择使用的小度量的一个吸引人的属性是,它也可以在正则化理论的上下文中,从而导致该解在某种程度上取决于所使用的特定内核而被解释为最大平滑【3】


我们的方法的主要灵感来自 Vapnik和合作者的早期工作。他们提出了一种算法,该算法通过使用超平面将其与原点分离来表征一组未标记的数据点【9】。但是,无论从算法还是从那时开始的统计学习理论的理论发展来看,他们都迅速转向了两类分类问题。从算法的角度来看,我们可以找出原始方法的两个缺点,这些缺点可能导致该放下的研究停止了三十多年。首先,原始算法仅限于输入空间中的线性决策规则,其次,无法处理离群值,结合起来,这些限制确实很严格-通用数据集不需要通过输入空间中的超平面与原点分离。我们合并的两个修改消除了这些缺点。首先,内核技巧通过非线性映射到高维特征空间中提供了更大的功能类别,从而增加了与原点分离的机会。特别是,使用高斯核(2),对于任何数据集 x1....xl 都存在这样的分类,x:要看清楚这一点,请注意,对于所有的 K(Xi, Xj) >0,因此所有点积均为正,暗示所有映射的模式都在同一个 orthant内。此外,由于所有的 i 的 k(Xi, Xj)=1 因此他们具有单位长度。因此他们与原点是可分离的。第二张修改允许出现异常值的可能性。我们使用 trick 结合了决策规则的“软性”,因此可以直接处理异常值。

我们认为我们的方法提出了一种具有良好计算复杂度的具体算法(凸二次规划),以解决迄今为止主要从理论角度进行研究的问题,具有广泛的实际应用。为了使该算法称为从业人员易于使用的黑盒方法,必须解决诸如选择内核参数(例如高斯内核的宽度)之类的问题,我们期望我们在本文中简要概述的理论将为这一艰巨的任务提供基础。
致谢 这项工作的一部分是由ARC和DFG(#Ja379 / 9-1)支持的,而BS是在澳大利亚国立大学和GMD FIRST期间完成的。 AS由Deutsche Forschungsgemeinschaft(Sm 62 / 1-1)资助。 感谢S.Ben David,C。Bishop,C。Schnörr和M. Tipping的有益讨论。

加载全部内容