前言

人们常说“物以类聚，人以群分”，在生物学中也对生物从界门纲目科属种中进行了划分。在统计学中，也有聚类分析法，通过把相似的对象通过静态分类的方法分成不同的组别或者更多的子集，从而让同一个子集中的成员都有相似的一些属性，然后对这些子集中的数据进行分析，其关键则在于聚类。这系列文章将来讲讲各种聚类方法，这篇开篇文章将介绍下聚类的相关概念以及最基本的算法 K-Means。

聚类

我们都知道，在机器学习中，一般分为有监督、无监督、半监督学习三类。其中无监督学习常用的方法便是聚类。

将一个数据集分为多类后，每一类又称为簇，同一簇中的样本尽可能的相似，而不同簇中的样本尽可能不同。即具有高类内相似性和低类间相似性的特点。

聚类的方法大致可分为两种

• 分区（Partitional algorithms）
  • 基于原型：K-Means，GMM等
  • 基于密度：DBACAN，MeanShift等
• 分层（Hierarchical algorithms）
  • 自顶向下
  • 自底向上

这里，就不禁产生一个疑问，我们以什么为标准进行聚类？这也就涉及到了相似度的问题，即我们如何判断两个样本数据是不是相似的？

如果数据特征只有二维，那我们把数据中的点放置在二维坐标系中，如果属于一类，那这些点肯定是会离得比较近，这个近实际上就是我们的相似度度量标准，即距离。那当特征维数增加，在超平面中来划分类，自然也可以通过距离来度量相似性。

常见的距离

• Minkowski 距离
  • \(D_{mk}(x,z)=(\sum_{i=1}^{n}|x_i-z_i|^p)^{\frac{1}{p}}\)
  • 当 \(p=2\) 时，为欧氏距离 \(D_{ed}(x,z)=||x-z||=\sqrt{\sum_{i=1}^{n}|x_i-z_i|^2}\)
  • 当 \(p=1\) 时，为曼哈顿距离（城市距离） \(D_{man}(x,z)=||x-z||_1=\sum_{i=1}^{n}|x_i-z_i|\)
  • 若 \(p=+\infty\) 时，为 sup 距离 \(D_{sup}=||x-z||_{\infty}=max_{i=1}^{n}|x_i-z_i|\)
• Hamming 距离
  • 当特征为二值特征时，Minkowski 距离又被称为 Hamming 距离
• 皮尔森相关系数
  • \(S_p(x,z)=\frac{\sum_{i=1}^{n}(x_i-\bar{x})(z_i-\bar{z})}{\sqrt{\sum_{i=1}^{n}(x_i-\bar{x})^2 \times \sum_{i=1}^{n}(z_i-\bar{z})^2}}\)
• 余弦距离
  • \(S_c(x,z)=\frac{X^Tz}{||x||||z||}\)

K-Means

算法流程

K-Means 算法很好理解，首先需要指定聚类簇的个数 K。随机设定 K 个聚类中心 \(\mu_1,\mu_2,...,\mu_K \in \mathbb{R}^n\) ，然后不断迭代更新这些中心点，直到收敛：

1. for i=1 to m

   计算 \(x^{(i)}\) 距离最近的聚类簇的中心，将其作为 \(x^{(i)}\) 的类别，即 \(y^{(i)}=\arg\min_k{||x^{(i)}-\mu_k||^2}\)

2. for k=1 to K

   更新聚类簇的中心，用所有属于第 k 个簇的样本的均值去更新 \(\mu_k\) ，即 \(\mu_k=avg(x^{(i)}|y^{(i)}=k)\)

从上面的介绍可以看出来， K-Means 的目标函数为
\[ J\left(y^{(1)}, \cdots, y^{(m)}, \mu_{1}, \cdots, \mu_{K}\right)=\frac{1}{m} \sum_{i=1}^{m}\left\|x^{(i)}-\mu_{y^{(i)}}\right\|^{2} \]

K 值选取

之前提到过 K 值是需要自己设定的，那么，我们要如何才能取到合适的 K 值呢？（之前面试给问到这个问题，当时一时间懵了。。。面试官说是可以算出来的一般选择在 \(\sqrt{\frac{n}{2}}\) 附近做调整，没试过真不太清楚）

一般有两种方式，分别是手肘法和轮廓系数法

手肘法

采用指标 SSE(sum of the sqared errors，误差平方和)
\[ SSE=\sum_{i-1}^{k}\sum_{p\in C_i}|p-\mu_i|^2 \]
其中，\(C_i\) 表示第 i 个簇，p为 \(C_i\) 中的样本点，\(\mu_i\) 为 \(C_i\) 的质心。

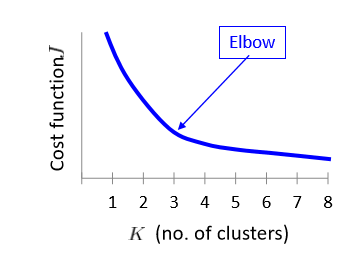
其核心思想是随着聚类数 k 的增大，样本划分不断精细，SSE 会不断减小。当 k 小于真实聚类树时，k 的增大会大幅度增加每个簇的聚合程度，SSE 的下降幅度会骤减，然后随着 k 值得继续增大而趋于平缓。

轮廓系数法

该方法的核心指标时轮廓系数（silhouette Coefficient），某个样本点 \(x_i\) 的轮廓系数定义为
\[ S=\frac{b-a}{max(a,b)} \]
其中，a 是 \(x_i\) 与同簇的其它样本的平均距离，称为凝聚度，b 是 \(x_i\) 与最近簇中所有样本的平均距离，称为分离度。最近簇的定义为
\[ C_j=\arg\min_{C_k}\frac{1}{n}\sum_{p\in C_k}|p-x_i|^2 \]
其中 p 是某个簇 \(C_k\) 中的样本。

求出所有样本的轮廓系数之后再求平均值就得到了平均轮廓系数，一般来说，簇内样本的距离越近，簇间样本距离越远，平均平均轮廓系数越大，效果越好。

代码实现

#随机初始化centroids
def kMeansInitCentroids(X, K):
    """
    随机初始化centroids
    :param X: 训练样本
    :param K: 聚类簇个数
    :return: 初始化的centroids
    """
    np.random.seed(5)
    
    i = np.random.randint(0, len(X), K)
    centroids = X[i, :]
    
    return centroids

def findClosestCentroids(X, centroids):
    """
    寻找每个样本离之最近的centroid
    :param X: 训练集
    :param centroids:聚类簇中心
    :return: 索引集
    """
    K = centroids.shape[0]
    m = X.shape[0]
    index = np.zeros((m))
    
    for i in range(m):
        dis = np.sum(np.power(X[i, :] - centroids, 2), axis=1)
        index[i] = np.argmin(dis)
    
    return index

def computeCentroids(X, index, K):
    """
    更新聚类簇中心
    :param X: 训练集
    :param index: 索引集
    :param K: 聚类簇个数
    :return: 更新的聚类簇中心
    """
    [m, n] = X.shape
    centroids = np.zeros((K, n))
    
    for i in range(K):
        idx = np.where(index==i)
        centroids[i, :] = np.mean(X[idx, :], axis=1)
    
    return centroids

centroids = kMeansInitCentroids(X, K)
l = 10 # 迭代次数
for i in range(l):
    
    #计算索引集index
    index = findClosestCentroids(X, centroids)
    
    #更新centroids
    centroids = computeCentroids(X, index, K)

结果图

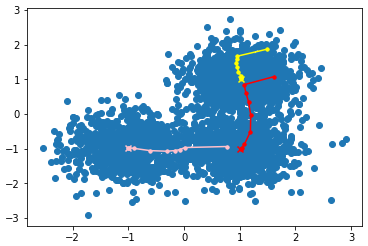
聚类中心移动