系列博客，原文在笔者所维护的github上：https://aka.ms/beginnerAI， 点击star加星不要吝啬，星越多笔者越努力。

第6章 多入单出的单层神经网路

6.0 线性二分类

6.0.1 提出问题

我们经常看到中国象棋棋盘中，用楚河汉界分割开了两个阵营的棋子。回忆历史，公元前206年前后，楚汉相争，当时刘邦和项羽麾下的城池，在中原地区的地理位置示意图如图6-1所示，部分样本数据如表6-1所示。

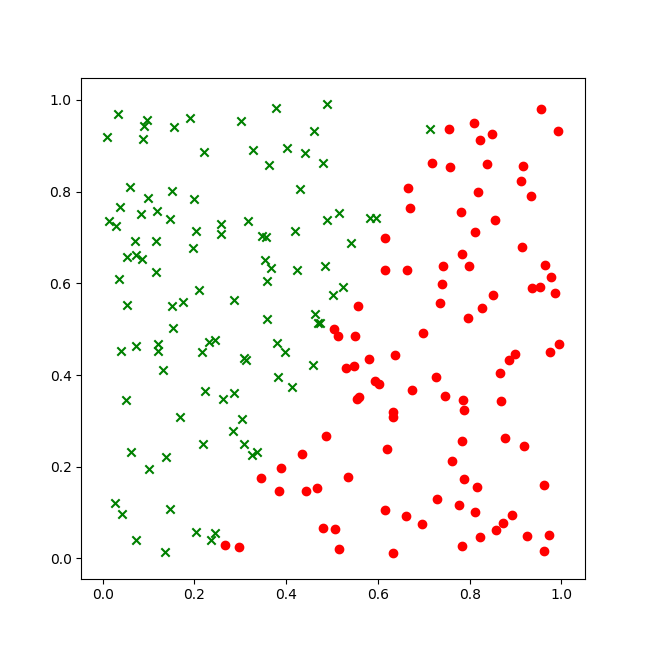
图6-1 样本数据可视化

1. 红色圆点，楚，项羽的城池
2. 绿色叉子，汉，刘邦的城池

表6-1 样本数据抽样

样本序号	X1:经度相对值	X2:纬度相对值	Y:1=汉, 0=楚
1	0.325	0.888	1
2	0.656	0.629	0
3	0.151	0.101	1
4	0.785	0.024	0
...	...	...	...
200	0.631	0.001	0

我们在上一章学习了特征归一化的方法。在本例中，中原地区的经纬度坐标其实应该是一个两位数以上的实数，比如(35.234, -122.455)。为了简化问题，我们已经把它们归一化到[0,1]之间了。

问题：

1. 经纬度相对坐标值为(0.58,0.92)时，属于楚还是汉？
2. 经纬度相对坐标值为(0.62,0.55)时，属于楚还是汉？
3. 经纬度相对坐标值为(0.39,0.29)时，属于楚还是汉？

读者可能会觉得这个太简单了，这不是有图吗？定位坐标值后在图上一比划，一下子就能找到对应的区域了。但是我们要求用机器学习的方法来解决这个看似简单的问题，以便将来的预测行为是快速准确的，而不是拿个尺子在图上去比划。

另外，本着用简单的例子说明复杂的原理的原则，我们用这个看似简单的例子，是想让读者对问题和解决方法都有一个视觉上的清晰认识，而这类可以可视化的问题，在实际生产环境中并不多见。

6.0.2 逻辑回归模型

回归问题可以分为两类：线性回归和逻辑回归。在第二步中，我们学习了线性回归模型，在第三步中，我们将一起学习逻辑回归模型。

逻辑回归的英文是Logistic Regression，逻辑回归是用来计算“事件=Success”和“事件=Failure”的概率。当因变量的类型属于二元（1 / 0，真/假，是/否）变量时，我们就应该使用逻辑回归。

回忆线性回归，使用一条直线拟合样本数据，而逻辑回归是“拟合”0或1两个数值，而不是具体的连续数值，所以它叫广义线性模型。逻辑回归又称logistic回归分析，常用于数据挖掘，疾病自动诊断，经济预测等领域。

例如，探讨引发疾病的危险因素，并根据危险因素预测疾病发生的概率等。以胃癌病情分析为例，选择两组人群，一组是胃癌组，一组是非胃癌组，两组人群必定具有不同的体征与生活方式等。因此因变量就为是否胃癌，值为“是”或“否”；自变量就可以包括很多了，如年龄、性别、饮食习惯、幽门螺杆菌感染等。

自变量既可以是连续的，也可以是分类的。然后通过logistic回归分析，可以得到自变量的权重，从而可以大致了解到底哪些因素是胃癌的危险因素。同时根据该权值可以根据危险因素预测一个人患癌症的可能性。

逻辑回归的另外一个名字叫做分类器，分为线性分类器和非线性分类器，本章中我们学习线性分类器。而无论是线性还是非线性分类器，又分为两种：二分类问题和多分类问题，在本章中我们学习二分类问题。线性多分类问题将会在下一章讲述，非线性分类问题在后续的步骤中讲述。

综上所述，我们本章要学习的路径是：回归问题->逻辑回归问题->线性逻辑回归即分类问题->线性二分类问题。

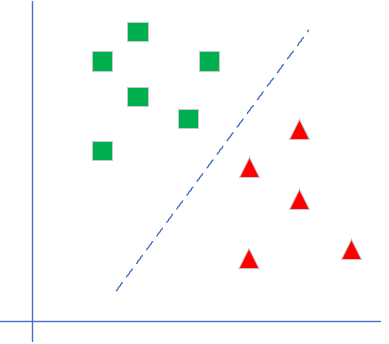
表6-2示意说明了线性二分类和非线性二分类的区别。

表6-2 直观理解线性二分类与非线性二分类的区别

线性二分类	非线性二分类

我们先学习如何解决线性二分类为标题，在此基础上可以扩展为非线性二分类问题。

系列博客，原文在笔者所维护的github上：https://aka.ms/beginnerAI， 点击star加星不要吝啬，星越多笔者越努力。

6.1 二分类函数

此函数对线性和非线性二分类都适用。

6.1.1 二分类函数

对率函数Logistic Function，即可以做为激活函数使用，又可以当作二分类函数使用。而在很多不太正规的文字材料中，把这两个概念混用了，比如下面这个说法：“我们在最后使用Sigmoid激活函数来做二分类”，这是不恰当的。在本书中，我们会根据不同的任务区分激活函数和分类函数这两个概念，在二分类任务中，叫做Logistic函数，而在作为激活函数时，叫做Sigmoid函数。

• 公式

\[Logistic(z) = \frac{1}{1 + e^{-z}} \rightarrow a\]

• 导数

\[Logistic'(z) = a(1 - a)\]

具体求导过程可以参考8.1节。

• 输入值域

\[(-\infty, \infty)\]

• 输出值域

\[(0,1)\]

• 函数图像（图6-2）

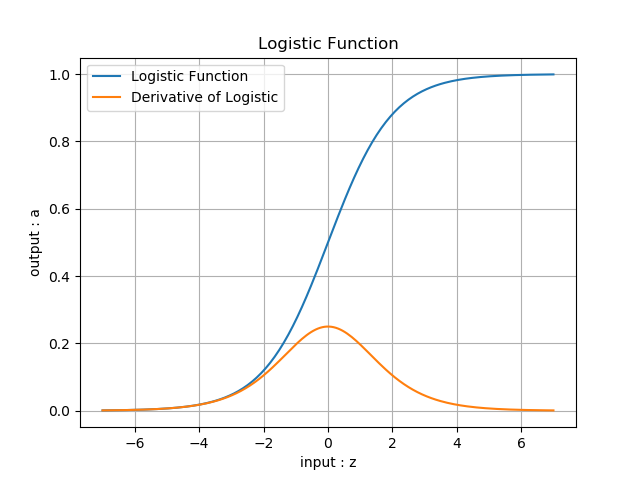
图6-2 Logistic函数图像

• 使用方式

此函数实际上是一个概率计算，它把\((-\infty, \infty)\)之间的任何数字都压缩到\((0,1)\)之间，返回一个概率值，这个概率值接近1时，认为是正例，否则认为是负例。

训练时，一个样本x在经过神经网络的最后一层的矩阵运算结果作为输入z，经过Logistic计算后，输出一个\((0,1)\)之间的预测值。我们假设这个样本的标签值为0属于负类，如果其预测值越接近0，就越接近标签值，那么误差越小，反向传播的力度就越小。

推理时，我们预先设定一个阈值比如0.5，则当推理结果大于0.5时，认为是正类；小于0.5时认为是负类；等于0.5时，根据情况自己定义。阈值也不一定就是0.5，也可以是0.65等等，阈值越大，准确率越高，召回率越低；阈值越小则相反，准确度越低，召回率越高。

比如：

• input=2时，output=0.88，而0.88>0.5，算作正例
• input=-1时，output=0.27，而0.27<0.5，算作负例

6.1.2 正向传播

矩阵运算

\[ z=x \cdot w + b \tag{1} \]

分类计算

\[ a = Logistic(z)={1 \over 1 + e^{-z}} \tag{2} \]

损失函数计算

二分类交叉熵损失函数：

\[ loss(w,b) = -[y \ln a+(1-y) \ln(1-a)] \tag{3} \]

6.1.3 反向传播

求损失函数对a的偏导

\[ \frac{\partial loss}{\partial a}=-[{y \over a}+{-(1-y) \over 1-a}]=\frac{a-y}{a(1-a)} \tag{4} \]

求a对z的偏导

\[ \frac{\partial a}{\partial z}= a(1-a) \tag{5} \]

求损失函数loss对z的偏导

使用链式法则链接公式4和公式5：

\[ \frac{\partial loss}{\partial z}=\frac{\partial loss}{\partial a}\frac{\partial a}{\partial z} \]
\[ =\frac{a-y}{a(1-a)} \cdot a(1-a)=a-y \tag{6} \]

我们惊奇地发现，使用交叉熵函数求导得到的分母，与Logistic分类函数求导后的结果，正好可以抵消，最后只剩下了\(a-y\)这一项。真的有这么巧合的事吗？实际上这是依靠科学家们的聪明才智寻找出了这种匹配关系，以满足以下条件：

1. 损失函数满足二分类的要求，无论是正例还是反例，都是单调的；
2. 损失函数可导，以便于使用反向传播算法；
3. 让计算过程非常简单，一个减法就可以搞定。

多样本情况

我们用三个样本做实例化推导：

\[Z= \begin{pmatrix} z_1 \\ z_2 \\ z_3 \end{pmatrix}, A=Logistic\begin{pmatrix} z_1 \\ z_2 \\ z_3 \end{pmatrix}= \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \]

\[ \begin{aligned} J(w,b)=&-[y_1 \ln a_1+(1-y_1)\ln(1-a_1)] \\ &-[y_2 \ln a_2+(1-y_2)\ln(1-a_2)] \\ &-[y_3 \ln a_3+(1-y_3)\ln(1-a_3)] \\ \end{aligned} \]
代入公式6结果：
\[ \begin{aligned} {\partial J(w,b) \over \partial Z}&= \begin{pmatrix} {\partial J(w,b) / \partial z_1} \\ {\partial J(w,b) / \partial z_2} \\ {\partial J(w,b) / \partial z_3} \end{pmatrix} \\ &=\begin{pmatrix} a_1-y_1 \\ a_2-y_2 \\ a_3-y_3 \end{pmatrix}=A-Y \end{aligned} \]

所以，用矩阵运算时可以简化为矩阵相减的形式：\(A-Y\)。

6.1.4 对数几率的来历

经过数学推导后可以知道，神经网络实际也是在做这样一件事：经过调整w和b的值，把所有正例的样本都归纳到大于0.5的范围内，所有负例都小于0.5。但是如果只说大于或者小于，无法做准确的量化计算，所以用一个对率函数来模拟。

说到对率函数，还有一个问题，它为什么叫做“对数几率”函数呢？

我们举例说明：假设有一个硬币，抛出落地后，得到正面的概率是0.5，得到反面的概率是0.5，这两个概率叫做probability。如果用正面的概率除以反面的概率，0.5/0.5=1，这个数值叫做odds，即几率。

泛化一下，如果正面的概率是a，则反面的概率就是1-a，则几率等于：

\[odds = \frac{a}{1-a} \tag{9}\]

上式中，如果a是把样本x的预测为正例的可能性，那么1-a就是其负例的可能性，a/(1-a)就是正负例的比值，称为几率(odds)，反映了x作为正例的相对可能性，而对几率取对数就叫做对数几率(log odds, logit)。

假设概率如表6-3。

表6-3 概率到对数几率的对照表

概率a	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
反概率 (1-a)	1	0.9	0.8	0.7	0.6	0.5	0.4	0.3	0.2	0.1	0
几率 odds	0	0.11	0.25	0.43	0.67	1	1.5	2.33	4	9	\(\infty\)
对数几率 ln(odds)	N/A	-2.19	-1.38	-0.84	-0.4	0	0.4	0.84	1.38	2.19	N/A

可以看到几率的值不是线性的，不利于分析问题，所以在表中第4行对几率取对数，可以得到一组成线性关系的值，并可以用直线方程\(xw+b\)来表示，即：

\[ \ln(odds) = \ln \frac{a}{1-a}= xw + b \tag{10} \]

对公式10两边取自然指数：

\[ \frac{a}{1-a}=e^{xw+b} \tag{11} \]

\[ a=\frac{1}{1+e^{-(xw+b)}} \]

令\(z=e^{-(xw+b)}\)：

\[ a=\frac{1}{1+e^{-z}} \tag{12} \]

公式12就是公式2！对数几率的函数形式可以认为是这样得到的。

以上推导过程，实际上就是用线性回归模型的预测结果来逼近样本分类的对数几率。这就是为什么它叫做逻辑回归(logistic regression)，但其实是分类学习的方法。这种方法的优点如下：

• 直接对分类可能性建模，无需事先假设数据分布，避免了假设分布不准确所带来的问题；
• 不仅预测出类别，而是得到了近似的概率，这对许多需要利用概率辅助决策的任务很有用；
• 对率函数是任意阶可导的凸函数，有很好的数学性，许多数值优化算法都可以直接用于求取最优解。

系列博客，原文在笔者所维护的github上：https://aka.ms/beginnerAI， 点击star加星不要吝啬，星越多笔者越努力。

6.2 用神经网络实现线性二分类

我们先看看如何用神经网络在两组不同标签的样本之间画一条明显的分界线。这条分界线可以是直线，也可以是曲线。这就是二分类问题。如果只画一条分界线的话，无论是直线还是曲线，我们可以用一支假想的笔（即一个神经元），就可以达到目的，也就是说笔的走向，完全依赖于这一个神经元根据输入信号的判断。

再看楚汉城池示意图，在两个颜色区域之间似乎存在一条分割的直线，即线性可分的。

1. 从视觉上判断是线性可分的，所以我们使用单层神经网络即可；
2. 输入特征是经度和纬度，所以我们在输入层设置两个输入X1=经度，X2=维度；
3. 最后输出的是一个二分类，分别是楚汉地盘，可以看成非0即1的二分类问题，所以我们只用一个输出单元就可以了。

6.2.1 定义神经网络结构

根据前面的猜测，看来我们只需要一个二入一出的神经元就可以搞定。这个网络只有输入层和输出层，由于输入层不算在内，所以是一层网络，见图6-3。

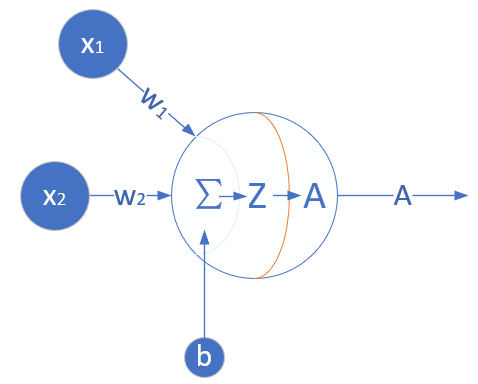
图6-3 完成二分类任务的神经元结构

与上一章的网络结构图的区别是，这次我们在神经元输出时使用了分类函数，所以有个A的输出，而不是以往的Z的直接输出。

输入层

输入经度\(x_1\)和纬度\(x_2\)两个特征：

\[ X=\begin{pmatrix} x_{1} & x_{2} \end{pmatrix} \]

权重矩阵

输入是2个特征，输出一个数，则\(W\)的尺寸就是2x1：

\[ W=\begin{pmatrix} w_{1} \\ w_{2} \end{pmatrix} \]

B的尺寸是1x1，行数永远是1，列数永远和W一样。

\[ B=\begin{pmatrix} b_{1} \end{pmatrix} \]

输出层

\[ \begin{aligned} z &= X \cdot W + B =\begin{pmatrix} x_1 & x_2 \end{pmatrix} \begin{pmatrix} w_1 \\ w_2 \end{pmatrix} + (b_1) \\ &=x_1 \cdot w_1 + x_2 \cdot w_2 + b_1 \end{aligned} \tag{1} \]
\[a = Logistic(z) \tag{2}\]

损失函数

二分类交叉熵损失函数：

\[ loss(w,b) = -[yln a+(1-y)ln(1-a)] \tag{3} \]

6.2.2 反向传播

我们在6.1节已经推导了loss对z的偏导数，结论为\(A-Y\)。接下来，我们求loss对w的导数。本例中，w的形式是一个2行1列的向量，所以求w的偏导时，要对向量求导：

\[ \frac{\partial loss}{\partial w}= \begin{pmatrix} {\partial loss / \partial w_1} \\ {\partial loss / \partial w_2} \end{pmatrix} \]
\[ =\begin{pmatrix} \frac{\partial loss}{\partial z}\frac{\partial z}{\partial w_1} \\ \\ \frac{\partial loss}{\partial z}\frac{\partial z}{\partial w_2} \end{pmatrix} = \begin{pmatrix} (a-y)x_1 \\ (a-y)x_2 \end{pmatrix} \]
\[ =(x_1 \ x_2)^T (a-y) \tag{4} \]

上式中\(x_1x_2\)是一个样本的两个特征值。如果是多样本的话，公式4将会变成其矩阵形式，以3个样本为例：

\[ {\partial J(w,b) \over \partial w}= \begin{pmatrix} x_{11} & x_{12} \\ x_{21} & x_{22} \\ x_{31} & x_{32} \end{pmatrix}^T \begin{pmatrix} a_1-y_1 \\ a_2-y_2 \\ a_3-y_3 \end{pmatrix} \]
\[ =X^T(A-Y) \tag{5} \]

6.2.3 代码实现

我们先第5章的HelperClass5中，把一些已经写好的类copy过来，然后稍加改动，就可以满足我们的需要了。

由于以前我们的神经网络只会做线性回归，现在多了一个做分类的技能，所以我们加一个枚举类型，可以让调用者通过指定参数来控制神经网络的功能。

class NetType(Enum):
    Fitting = 1,
    BinaryClassifier = 2,
    MultipleClassifier = 3,

然后在超参类里把这个新参数加在初始化函数里：

class HyperParameters(object):
    def __init__(self, eta=0.1, max_epoch=1000, batch_size=5, eps=0.1, net_type=NetType.Fitting):
        self.eta = eta
        self.max_epoch = max_epoch
        self.batch_size = batch_size
        self.eps = eps
        self.net_type = net_type

再增加一个Logistic分类函数：

class Logistic(object):
    def forward(self, z):
        a = 1.0 / (1.0 + np.exp(-z))
        return a

以前只有均方差函数，现在我们增加了交叉熵函数，所以新建一个类便于管理：

class LossFunction(object):
    def __init__(self, net_type):
        self.net_type = net_type
    # end def

    def MSE(self, A, Y, count):
        ...

    # for binary classifier
    def CE2(self, A, Y, count):
        ...

上面的类是通过初始化时的网络类型来决定何时调用均方差函数(MSE)，何时调用交叉熵函数(CE2)的。

下面修改一下NeuralNet类的前向计算函数，通过判断当前的网络类型，来决定是否要在线性变换后再调用sigmoid分类函数：

class NeuralNet(object):
    def __init__(self, params, input_size, output_size):
        self.params = params
        self.W = np.zeros((input_size, output_size))
        self.B = np.zeros((1, output_size))

    def __forwardBatch(self, batch_x):
        Z = np.dot(batch_x, self.W) + self.B
        if self.params.net_type == NetType.BinaryClassifier:
            A = Sigmoid().forward(Z)
            return A
        else:
            return Z

最后是主过程：

if __name__ == '__main__':
    ......
    params = HyperParameters(eta=0.1, max_epoch=100, batch_size=10, eps=1e-3, net_type=NetType.BinaryClassifier)
    ......

与以往不同的是，我们设定了超参中的网络类型是BinaryClassifier。

6.2.4 运行结果

图6-4所示的损失函数值记录很平稳地下降，说明网络收敛了。

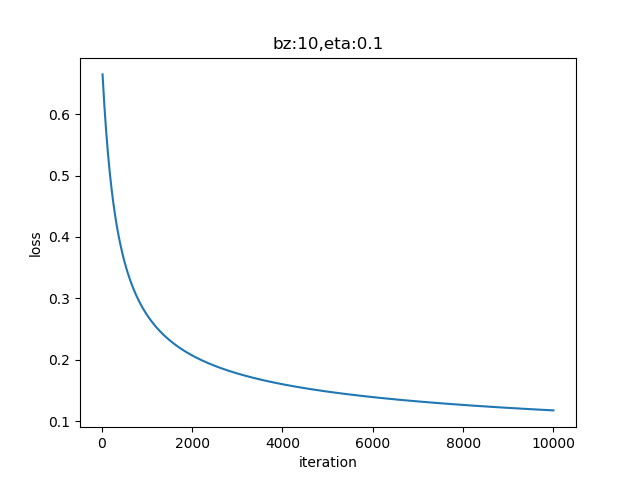
图6-4 训练过程中损失函数值的变化

最后几行的打印输出：

......
99 19 0.20742586902509108
W= [[-7.66469954]
 [ 3.15772116]]
B= [[2.19442993]]
A= [[0.65791301]
 [0.30556477]
 [0.53019727]]

打印出来的W,B的值对我们来说是几个很神秘的数字，下一节再解释。A值是返回的预测结果：

1. 经纬度相对值为(0.58,0.92)时，概率为0.65，属于汉；
2. 经纬度相对值为(0.62,0.55)时，概率为0.30，属于楚；
3. 经纬度相对值为(0.39,0.29)时，概率为0.53，属于汉。

分类的方式是，可以指定当A > 0.5时是正例，A <= 0.5时就是反例。有时候正例反例的比例不一样或者有特殊要求时，也可以用不是0.5的数来当阈值。

代码位置

ch06, Level1

系列博客，原文在笔者所维护的github上：https://aka.ms/beginnerAI， 点击star加星不要吝啬，星越多笔者越努力。

6.3 线性二分类原理

6.3.1 线性分类和线性回归的异同

此原理对线性和非线性二分类都适用。

回忆一下前面学习过的线性回归，通过用均方差函数的误差反向传播的方法，不断矫正拟合直线的角度（Weights）和偏移（Bias），因为均方差函数能够准确地反映出当前的拟合程度。那么在线性分类中，我们能不能采取类似的方法呢？

线性分类，试图在含有两种样本的空间中划出一条分界线，让双方截然分开，就好像是中国象棋的棋盘中的楚河汉界一样。与线性回归相似的地方是，两者都需要划出那条“直线”来，但是不同的地方也很明显，见表6-4。

表6-4 线性回归和线性分类的比较

	线性回归	线性分类
相同点	需要在样本群中找到一条直线	需要在样本群中找到一条直线
不同点	用直线来拟合所有样本，使得各个样本到这条直线的距离尽可能最短	用直线来分割所有样本，使得正例样本和负例样本尽可能分布在直线两侧

可以看到线性回归中的目标--“距离最短”，还是很容易理解的，但是线性分类的目标--“分布在两侧”，用数学方式如何描述呢？我们可以有代数和几何两种方式来描述。

6.3.2 二分类的代数原理

代数方式：通过一个分类函数计算所有样本点在经过线性变换后的概率值，使得正例样本的概率大于0.5，而负例样本的概率小于0.5。

基本公式回顾

下面我们以单样本双特征值为例来说明神经网络的二分类过程，这是用代数方式来解释其工作原理。

1. 正向计算

\[ z = x_1 w_1+ x_2 w_2 + b \tag{1} \]

1. 分类计算

\[ a={1 \over 1 + e^{-z}} \tag{2} \]

1. 损失函数计算

\[ loss = -[y \ln (a)+(1-y) \ln (1-a)] \tag{3} \]

用图6-5举例来说明计算过程。

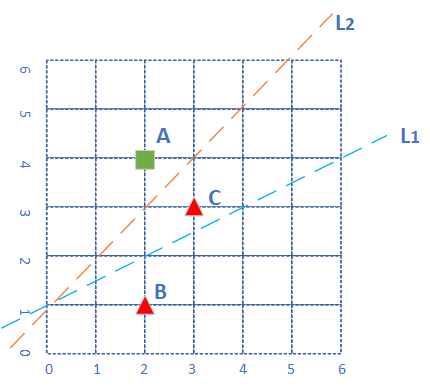
图6-5 不正确的分类线试图分类红绿两色样本点

平面上有三个点，分成两类，绿色方块为正类，红色三角为负类。各个点的坐标为：\(A(2,4)，B(2,1)，C(3,3)\)。

分类线为L1时

假设神经网络第一次使用\(L_1\)做为分类线，此时：\(w_1=-1,w_2=2,b=-2\)，我们来计算一下三个点的情况。

\(A\)点：

\[ z_A = (-1)\times 2 + 2 \times 4 -2 = 4 > 0 \tag{正确} \]

\(B\)点：

\[ z_B = (-1)\times 2 + 2 \times 1 -2 = -2 < 0 \tag{正确} \]

\(C\)点：

\[ z_C = (-1)\times 3 + 2 \times 3 -2 = 1 > 0 \tag{错误} \]

从6.1节中我们知道当\(z>0\)时，\(Logistic(z) > 0.5\)为正例，反之为负例，所以我们只需要看三个点的\(z\)值是否大于0或小于0就可以了，不用再计算\(Logistic\)的函数值。

其中，\(A、B\)点是处于正确的分类区，而\(C\)点处于错误的分类区。此时\(C\)点的损失函数值为（注意\(C\)的标签值\(y=0\)）：

\[ a_C = Sigmoid(z_C) = 0.731 \]

\[ loss_Z = -(0 \cdot \ln(0.731) + 1 \cdot \ln(1-0.731))=1.313 \]

读者可能对1.313这个值没有什么概念，是大还是小呢？我们不妨计算一下分类正确的\(A、B\)点的坐标：

\[ loss_A = 0.018, \quad loss_B = 0.112 \]

可见，对于分类正确的\(A、B\)点来说，其损失函数值比\(C\)点要小很多，所以对于\(C\)点的反向传播的力度就大。对比总结如表6-5。

表6-5 对比三个点在各个环节的计算值

点	坐标值	z值	a值	y值	loss值	分类情况
A	(2,4)	4	0.982	1	0.018	正确
B	(2,1)	-2	0.119	0	0.112	正确
C	(3,3)	1	0.731	0	1.313	错误

• 在正例情况y=1时，a如果越靠近1，表明分类越正确，此时损失值会越小。点A就是这种情况：a=0.982，距离1不远；loss值0.018，很小；
• 在负例情况y=0时，a如果越靠近0，表明分类越正确，此时损失值会越小。点B就是这种情况：a=0.119，距离0不远；loss值0.112，不算很大；
• 点C是分类错误的情况，a=0.731，应该是小于0.5的，却距离0远，距离1反而近，所以它的loss=1.313，从与其它两个点比较的相对值来看，是非常大的，这样误差就大，反向传播的力度也大。

分类线为L2时

我们假设经过反向传播后，神经网络把直线的位置调整到\(L_2\)，以\(L_2\)做为分类线，即\(w_1=-1,w_2=1,b=-1\)，则三个点的\(z\)值都会是符合其分类的：

\[ z_A = (-1)\times 2 + 1 \times 4 -1 = 1 > 0 \tag{正确} \]

\[ z_B = (-1)\times 2 + 1 \times 1 -1 = -2 < 0 \tag{正确} \]

\[ z_C = (-1)\times 3 + 1 \times 3 -1 = -1 < 0 \tag{正确} \]

这里可能会产生一个疑问：既然用\(z\)值是否大于0这个条件就可以判断出分类是否正确，那么二分类理论中为什么还要用\(Logistic\)函数做一次分类呢？

原因是这样的：只有\(z\)值的话，我们只能知道是大于0还是小于0，并不能有效地进行反向传播，也就是说我们无法告诉神经网络反向传播的误差的力度有多大。比如\(z=5\)和\(z=-1\)相比，难度意味着前者的力度是后者的5倍吗？

而有了\(Logistic\)分类计算后，得到的值是一个\((0,1)\)之间的概率，比如：当\(z=5\)时，\(Logistic(5) = 0.993\)；当\(z=-1\)时，\(Logistic(-1)=0.269\)。这两个数值的含义是这两个样本在分类区内的概率，前者概率为99.3%，偏向正例，后者概率为26.9%，偏向负例。然后再计算损失函数，就可以得到神经网络可以理解的反向传播误差，比如上面曾经计算过的\(loss_A、loss_B、loss_C\)。

6.3.3 二分类的几何原理

几何方式：让所有正例样本处于直线的上方，所有负例样本处于直线的下方，尽可能处于双方的中间。

二分类函数的几何作用

二分类函数的最终结果是把正例都映射到图6-6中的上半部分的曲线上，而把负类都映射到下半部分的曲线上。

图6-6 Logistic函数把输入的点映射到(0,1)区间内实现分类

我们用正例来举例：

\[a = Logistic(z) = {1 \over 1 + e^{-z}} > 0.5\]

做公式变形，两边取自然对数，可以得到：

\[z > 0\]

即：
\[ z = x_1 \cdot w_1 + x_2 \cdot w_2 + b > 0 \]

对上式做一下变形，把\(x_2\)放在左侧，其他项放在右侧（假设\(w_2>0\)，则不等号方向不变）：
\[ x_2 > - {w_1 \over w_2}x_1 - {b \over w_2} \tag{5} \]

简化一下两个系数，令\(w'=-w1/w2，b'=-b/w2\)：

\[ x_2 > w' \cdot x_1 + b' \tag{6} \]

公式6用几何方式解释，就是：有一条直线，方程为\(z = w' \cdot x_1+b'\)，所有的正例样本都处于这条直线的上方；同理可得所有的负例样本都处于这条直线的下方。

图6-7 用直线分开的两类样本

我们再观察一下分类正确的图，如图6-7所示。假设绿色方块为正类：标签值\(y=1\)，红色三角形为负类：标签值\(y=0\)。从几何关系上理解，如果我们有一条直线，其公式为：\(z = w' \cdot x_1+b'\)，如图中的虚线\(L_1\)所示，则所有正类的样本的\(x_2\)都大于\(z\)，而所有的负类样本的\(x_2\)都小于\(z\)，那么这条直线就是我们需要的分割线。

这就说明神经网络的工作原理和我们在二维平面上的直观感觉是相同的，即当样本处于直线上方时，会被判为正例；反之则是负例。

我们还有一个额外的收获，即：

\[w' = - w1 / w2 \tag{7}\]

\[b' = -b/w2 \tag{8}\]

我们可以使用神经网络计算出\(w_1，w_2，b\)三个值以后，换算成\(w'，b'\)，以便在二维平面上画出分割线，来直观地判断神经网络训练结果的正确性。

思考与练习

1. 在推导公式5时，假设 \(w_2 > 0\)，这样做有什么问题吗？如果假设 \(w_2<0\) 会是什么情况？

系列博客，原文在笔者所维护的github上：https://aka.ms/beginnerAI， 点击star加星不要吝啬，星越多笔者越努力。

6.4 二分类结果可视化

6.4.1 可视化的重要性

我们虽然得到了结果，但都是一些神秘的数字，我们如何知道它们是正确还是错误的呢？

后面我们会讲到，在实际的工程实践中，一般我们会把样本分成训练集、验证集、测试集，用测试集来测试训练结果的正确性。在本例中我们没有这样做，原因有二：

1. 样本数据量比较少，一共只有200个样本，如果再分成两部分，会造成数据集覆盖不全面，存在很大的差异，对训练、验证、测试都没有帮助
2. 由于本例的数据特征比较少，所以我们有更好的手段：可视化。在神经网络学习初期，可视化的训练过程与结果会对读者有巨大的帮助。

神经网络的可视化，说简单也很简单，说难也很难，关键是对框架系统的理解，对运行机制和工作原理的理解，掌握了这些，可视化就会使一件轻而易举且令人愉快的事情。

6.4.2 权重值的含义

在6.2节中的训练结果如下，这几个关于W,B数字如何解读呢？

W= [[-7.66469954]
 [ 3.15772116]]
B= [[2.19442993]]
A= [[0.65791301]
 [0.30556477]
 [0.53019727]]

在6.1节中我们一起学习了线性二分类的原理，其中提到了如果我们能够根据训练结果，在图上画出一条直线来分割正例和负例两个区域，是不是就很直观了呢？

\[ z = x_{1} \cdot w_1 + x_{2} \cdot w_2 + b \tag{1} \]
\[ a=Logistic(z) \tag{2} \]

对公式2来说，当a大于0.5时，属于正例（属于汉），当a小于0.5时，属于负例（属于楚）。那么a=0.5时，就是楚汉边界啦！

\[a = 0.5, 相当于z=0\]
\[z = x_{1} \cdot w_1 + x_{2} \cdot w_2 + b = 0\]

把x2留在等式左侧，其它的挪到右侧去，就可以得到一条直线的方程了：

\[x_{2} \cdot w_2 = -x_{1} \cdot w_1 - b\]
\[x_2 = -{w_1 \over w_2}x_1 - {b \over w_2} \tag{3}\]

好了，这就是标准的直线方程\(y=ax+b\)的形式了。这个公式等同于二分类原理中的公式7，8。

6.4.3 代码实现

用Python代码实现公式3如下：

def draw_split_line(net,):
    b12 = -net.B[0,0]/net.W[1,0]
    w12 = -net.W[0,0]/net.W[1,0]
    print(w12,b12)
    x = np.linspace(0,1,10)
    y = w12 * x + b12
    plt.plot(x,y)
    plt.axis([-0.1,1.1,-0.1,1.1])
    plt.show()

上面代码中的计算w12,b12就是根据公式3来的，只不过我们的W的定义是(w1, w2)，而python是zero-based，所以：
\(w_1 = W[0,0]，w_2 = W[0,1]，b = B[0,0]\)。

同时需要展示样本数据，以便判断分割线和样本数据的吻合程度：

def draw_source_data(net, dataReader):
    fig = plt.figure(figsize=(6.5,6.5))
    X,Y = dataReader.GetWholeTrainSamples()
    for i in range(200):
        if Y[i,0] == 1:
            plt.scatter(X[i,0], X[i,1], marker='x', c='g')
        else:
            plt.scatter(X[i,0], X[i,1], marker='o', c='r')
        #end if
    #end for

最后还可以显示一下三个预测点的位置，看看是否正确：

def draw_predicate_data(net):
    x = np.array([0.58,0.92,0.62,0.55,0.39,0.29]).reshape(3,2)
    a = net.inference(x)
    print("A=", a)
    for i in range(3):
        if a[i,0] > 0.5:
            plt.scatter(x[i,0], x[i,1], marker='^', c='g', s=100)
        else:
            plt.scatter(x[i,0], x[i,1], marker='^', c='r', s=100)
        #end if
    #end for

主程序：

# 主程序
if __name__ == '__main__':
    ......
    # show result
    draw_source_data(net, reader)
    draw_predicate_data(net)
    draw_split_line(net)
    plt.show()

6.4.4 运行结果

图6-8为二分类结果。

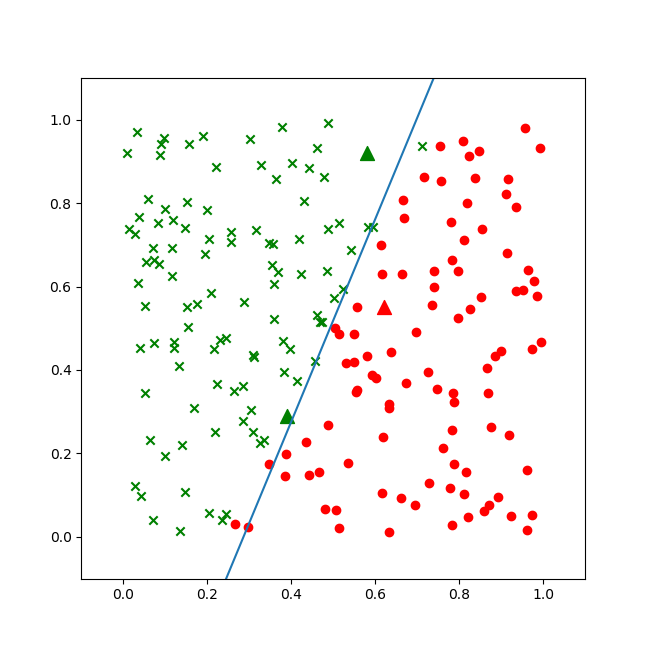
图6-8 稍有欠缺的二分类结果

虽然蓝色的分割线大体分开了楚汉两国，但是细心的读者会发现在上下两端，还是绿点在分割线右侧，而红点在分割线左侧的情况。这说明我们的神经网络的训练精度不够。所以，稍微改一下超参，再训练一遍：

params = HyperParameters(eta=0.1, max_epoch=10000, batch_size=10, eps=1e-3, net_type=NetType.BinaryClassifier)

把max_epoch从100改成了10000，再跑一次。

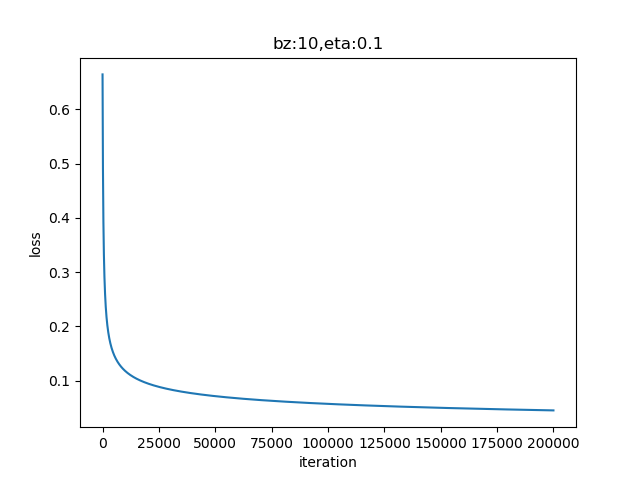
图6-9 训练过程中损失函数值的变化

从图6-9的曲线看，损失函数值一直在下降，说明网络还在继续收敛。再看图6-10的直线位置，已经比较完美地分开了红色和绿色区域。

图6-10 比较完美的二分类的结果

三个三角点是求解问题的三个坐标，其中第三个三角点处于分割线附近，用肉眼不是很容易分得出来，看打印输出：

W= [[-42.62417571]
 [ 21.36558218]]
B= [[10.5773054]]
A= [[0.99597669]
 [0.01632475]
 [0.53740392]]
w12= 1.994992477013739
b12= -0.49506282174794675

前两个点的概率分别是0.995和0.016，可以明确地区分正例负例，第三个点是0.537，大于0.5，可以算作正例。

在matplot的绘图控件中，我们也可以放大局部观察，可以图6-11的细节。

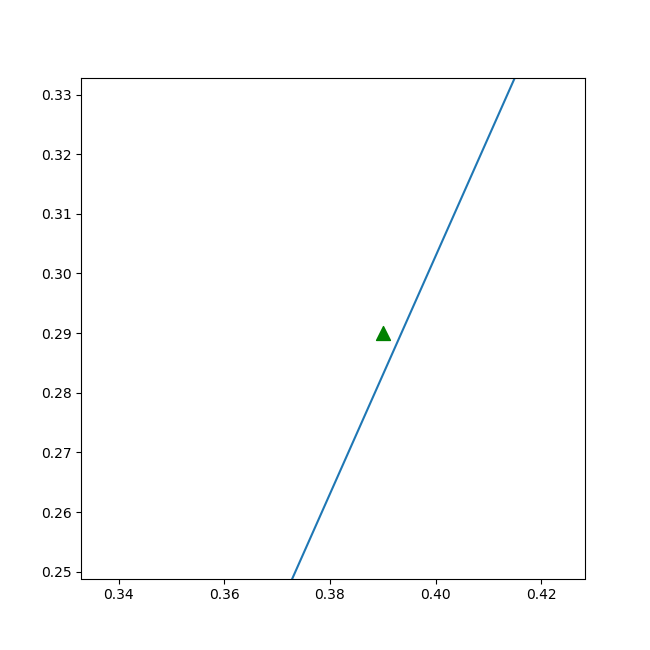
图6-11 放大后的细节，绿色点确实在直线左侧，分类正确

第三个点位于左侧正例区域。

好了，我们已经自信满满地找到了解释神经网络工作的原理，有数值计算验证，有公式推导，有图形显示，至少可以自圆其说了。但实际情况是不是这样呢？有没有更高深的原理还没有接触到呢？暂且留下这个问题，留在以后的章节去继续学习。

代码位置

ch06, Level2