Linux折腾记（十七）：适合数值计算的语言需要具备什么样的特色

　　2015年1月，我继续徜徉在数值计算的世界。这段时间里，我抽空看了Python科学计算和数值分析方面的书，也仔细研读了Octave的用户手册，甚至连古老的Fortran、新兴的R语言我都去逐一了解。对于数值计算的库，我了解了一下Boost的uBLAS，以前也用过OpenCV，当然，了解最多的还是Python中的NumPy、SciPy和pandas。

　　前几篇随笔搞了不少工具论，所以今天我就专门来论一论编程语言。我的这个Linux江湖系列是一会儿方法论一会儿工具论，每过一段时间也谈谈编程语言。今天谈的内容是我对适合做数值计算的编程语言的一些看法，主要是一些思路方面的东西，不评论具体语言的优劣。另外，我是想到哪儿写到哪儿，如果有什么不对的地方欢迎大家指正。

　　如果数值计算仅仅只是两个标量之间的加减乘除，那就不需要我在这里浪费口舌了。向量啊、矩阵啊、多维数组啊什么，才是数值计算真正的主角。所以，适合做数值计算的编程语言必须有一个好的方式表示数组，特别是多维数组。哪种方式好呢？是这样：

还是这样：

　　看似没有什么差别，但是如果你想获取数组a的形状呢？比如这样：

或者再更进一步，想改变数组a的形状呢？比如这样：

　　在上面的代码中，“?”究竟应该用什么代替呢？

　　如果让我给出答案，我会说：要用元组。很多编程语言中都有元组的概念，比如Python。元组就是用逗号隔开的几个值，可以加圆括号，也可以不加。我觉得加上圆括号后可读性更好。比如(a,b)是元组，(3,4,5)也是元组。如果写成[3,4,5]那就是数组了，在Python中，也称之为列表。不过Python的列表功能比数组要强大，因为数组只能保存同一种数据类型的值，而列表可以保存任何对象。数组一般情况下不能动态改变长度，而列表可以。Octave语言中使用cell array这个术语来表示可以保存不同类型对象的容器。Octave中的数组和矩阵是可以动态改变长度的。C语言的数组没有动态改变长度这个功能，而如果使用C++的话，则必须使用vector<>模板类。

　　我认为，一个好的编程语言必须要有“元组”这个一个概念，必须能够用好大括号、中括号和小括号。在有没有元组这个问题上，很多语言做得不好，C语言没有，C++也没有，Java没有，C#这个有很多新功能的语言也没有，不要告诉我有Tuple<>模板类可以用，那个真的没有语言内置的元组功能好。在能不能用好大中小括号这个问题上，C语言就做得不好。你看它不管是初始化数组，还是初始化struct，都是用大括号。而Python和JSON就做得很好嘛，初始化数组用中括号，初始化对象或字典的时候采用大括号。如果加上小括号表示元组，那就齐活儿了。

　　数值计算可以针对标量、一维数组、二维数组以及n维数组进行。数组可以如下组织，如下图：

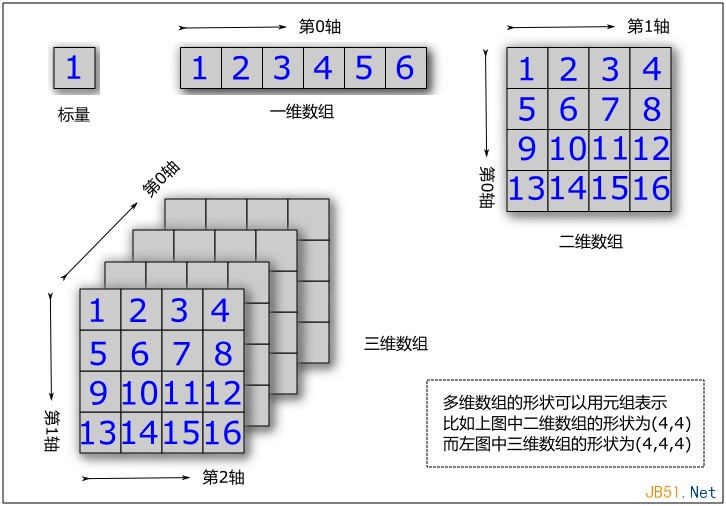
　　元组最大的用途就是可以用来表示数组的形状了。比如一维数组的形状为(n,)，请注意其中的逗号不能省略。二维数组的形状(m,n)，三维数组的形状(m,n,k)，依次类推。另外，元组可以用来对数组中的元素进行索引。比如：

　　元组还有一个很大的用途，那就是可以让一个函数返回多个值。C语言在这个方面是做得比较丑陋的，如果一个函数要返回多个值，只能给这个函数传指针或者多重指针作为参数，C++可以传引用，C#更加画蛇添足，专门有一个out关键字用来修饰函数的参数。微软你真是的，你既然能想到out，你就不能想到元组吗？常见的例子，比如meshgrid()函数可以同时初始化两个数组，peak()函数可以同时初始化三个数组。你看它们用元组多方便：

 　　另外，元组还可以这样用，比如交换两个变量的值：

　　在数值计算中，数组的初始化也是非常重要的一环。如果像C语言这样写：

估计很多人是要骂娘的。这样写：

也不优雅。我只是想初始化一个数组而已，怎么就非得要写一个循环呢？如果是二维数组呢，就得两层循环，三维数组就得三层。真的是太闹心了。

　　另外，如前所述，我也不喜欢在初始化数组的时候用大括号。我觉得中括号就是为数组而生。比如这样：

这就是一个一维数组，但是如果这样写：

就是一个行向量。如果写成这样：

那么这就是一个列向量，如下图：

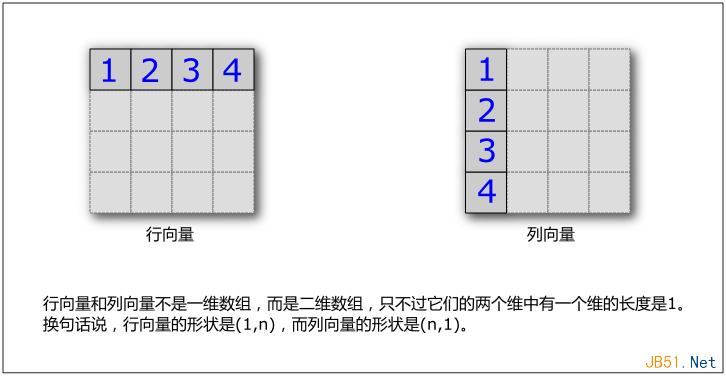
 　　当然，上面的示例只有四个数字，这么写一写无可厚非。如果是很多数字呢？或者很多维的数组呢？这时就必须得用到很多初始化函数了，而且这些初始化函数最好能接受元组作为参数来决定数组的形状。比如这样：

　　其它的初始化函数还有linspace()、logspace()、ones()、zeros()、eyes()等等。这些函数还可以配合reshape()使用，比如这样：

　　在所有的这些初始化中，元组都是重要的组成部分。

　　其实，range除了可以是一个函数，还可以更省点儿事，像这样写：

　　在某些语言中，也把这个功能叫切片。其实就是“:”的灵活运用，有标点符号可以用当然不能浪费嘛。使用切片，只需要指定起始值、终止值和步长，就可以获得一个数字序列。

　　但是，“:”最大的用途并不是用来对数组进行初始化，而是对数组进行索引。比如，a是一个三维数组，可以通过切片来获取其中的一部分数据。见下面的代码：

　　切片除了可以指定起始值和终止值外，也可以指定步长。当然，也可以只用一个单独的“:”，代表取这一整个轴。关于轴的概念，可以看我前面的图片。见下面这样的代码：

　　在对多维数组进行加减乘除的时候，如果使用传统的像C这样的语言，则避免不了要写循环。比如要计算两个多维数组的加法，不得不写这样的代码：

　　上面的代码当然远不如下面这样的代码简洁：

　　所以不写循环基本上就成了所有数值计算语言的标准配置。Matlab和Octave是这样，NumPy是这样，R语言也是这样。C++也在追求这样，因为C++中有运算符重载的功能，所以可以对矩阵类重载加减乘除运算符。但是C++中运算符的基础设施有缺陷，比如它没有乘方运算符（幂运算符），在Octave和NumPy中，都可以这样计算$x^y$：x**y。但是在C++中，只有使用函数power(x, y)。不要想^运算符，它是一个位运算符，所以取幂只有使用**了。另外，多维数组运算还有特例，比如二维数组之间加减乘除，既可以是逐元素的加减乘除，也可以是矩阵的加减乘除。向量计算也有特例，既可以是逐元素加减乘除，也可能是向量内积（点乘）。如果正好是长度为3的向量，还可以计算叉乘。这些运算符都需要重新定义，所以虽然C++有重载运算符的机制，但是因为这些运算符完全超越了C++的基础设施，所以C++也没有办法写得很优雅。

　　不写循环还有一个优点，那就是可以对运算速度进行优化。优化是编译器或解释器的责任，写数值计算程序的人可以完全不用费心。编译器或解释器可采取的优化方式有可能是利用SSE等多媒体指令集，也可能是发挥多核CPU的多线程优势，甚至是使用GPGPU计算都有可能。如果用户非要写成C语言那样的循环，而他又不会内联汇编或OpenMP的话，那么就谈不上什么运算速度的优化了。

　　不写循环，直接把两个多维数组进行加减乘除当然省事。但是如果两个数组的形状不一样呢？比如一个二维数组加一个行向量，或一个二维数组加一个列向量，甚至是数组加减乘除一个标量，会出现什么情况呢？

　　不用担心，在面向数值计算的语言中，一般都有“广播”这样一个特性。当两个数组的形状不一样时，形状比较小的那个往往可以在长度为1的维度上进行广播。如下图：

　　Fancy indexing，有的书上翻译成花式索引，但我认为叫奇异索引比较好。它就是指一个低维的数组，可以使用高维的数组进行索引，最后得到的结果是一个高维的数组。如果索引中含有切片，可能会得到一个更高维度的数组作为结果。

　　这个概念理解起来比较难。特别是再配合切片使用，更加增加其复杂性。所谓一图胜千言，先看普通索引的情况：

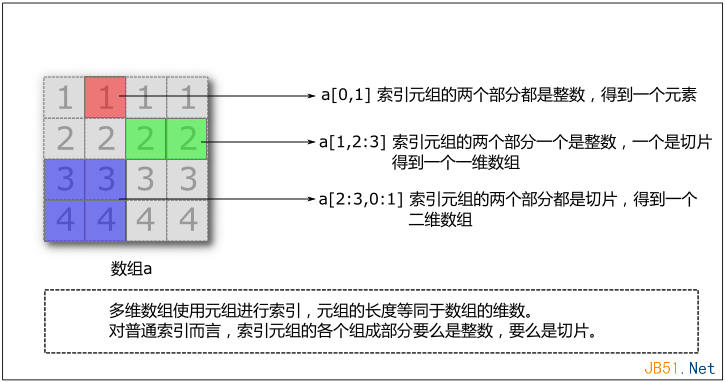
 　　前面提到，对多维数组进行索引的时候需要用到元组，元组的长度等同于数组的维数。对于普通索引而言，元组的各个部分要么是整数，要么是切片。而对于奇异索引而言，索引元组的各个组成部分都可能是多维数组或者切片。如果是多维数组，则最后得到的数组的形状和索引数组的形状相同，如果配合切片，则可能得到更高维的数组。如下图：

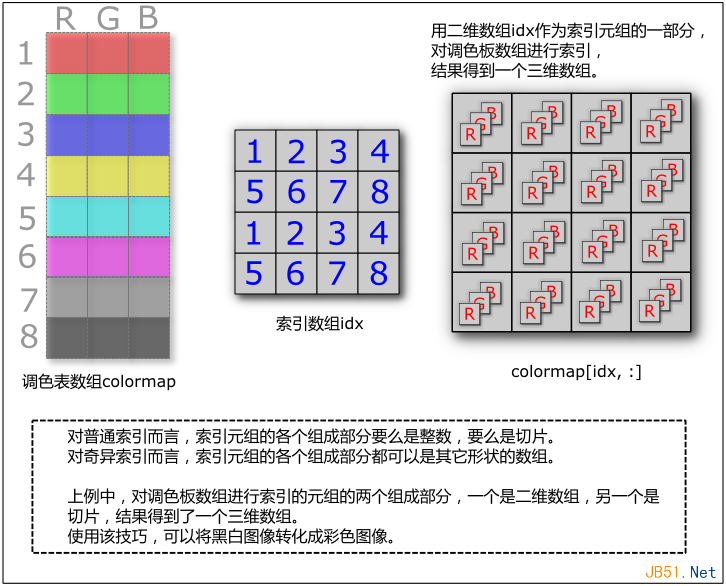
　　编程语言发展这么多年，一直在进化，也一直在相互靠拢。对于一个编程语言来说，是应该面向过程还是面向对象？是静态类型还是动态类型？这些都是值得思考的地方。但是在函数调用方面，有一些思想倒是可以学习。

　　在C语言这样比较古老的语言中，对于函数的参数来说，只有位置参数一种。也就是说，像一个函数传递参数的时候，只能正确的参数放到正确的位置，而且参数的个数必须和函数定义的相同。这是最原始的函数调用思想。

　　紧接着，在某些编程语言如Java、C#中，有了可选参数这个概念。但是可选参数要放到参数列表的最后面，而且必须提供默认值。当调用函数时如果指定了这个参数，则使用调用时指定的值，否则使用默认值。

　　但是我觉得适合数值计算的语言必须还得更进一步，提供关键字参数的功能。什么是关键字参数呢？比如对数据进行绘图的时候，需要指定线型、标签、标题等各种属性，可以这样调用函数：

　　每一个参数调用的时候都可以指定它的名字，这样我们就不用去死记各个参数的位置，是不是很方便呢？

　　对于一门编程语言而言，生态坏境很重要。在数值计算领域更是如此。因为很多数值计算的库都是专业的人士写给专业人士看的，比如物理专业的写物理领域的算法，气象专业的写气象专业的算法，所以不大可能有一个全面的官方的，像C或C++这样一个由ANSI定义的库。

　　广泛接受开源社区的贡献是一个比较好的办法。Perl是这样，Python也是这样，新兴的R语言也是这样。Perl有CPAN，Python有PyPI，R语言也有CRAN。至于Matlab，那更是有各种各样的工具包。

　　OK，就写这么多吧，还有其它的一些什么特色，我想到后再随时更新此文。

　　另外，本文中所有的图片都是在Ubuntu中使用Inkscape矢量图软件绘制而成。