直观理解为什么分类问题用交叉熵损失而不用均方误差损失?
shine-lee 人气:0目录
- 交叉熵损失与均方误差损失
- 损失函数角度
- softmax反向传播角度
- 参考
博客:blog.shinelee.me | 博客园 | CSDN
交叉熵损失与均方误差损失
常规分类网络最后的softmax层如下图所示,传统机器学习方法以此类比,
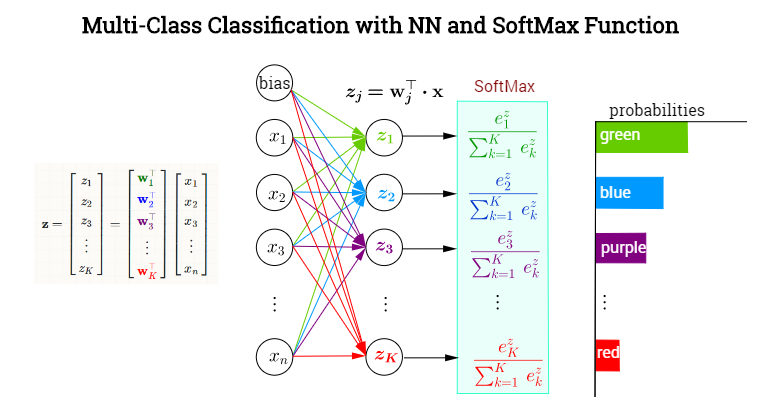
一共有\(K\)类,令网络的输出为\([\hat{y}_1,\dots, \hat{y}_K]\),对应每个类别的概率,令label为 \([y_1, \dots, y_K]\)。对某个属于\(p\)类的样本,其label中\(y_p=1\),\(y_1, \dots, y_{p-1}, y_{p+1}, \dots, y_K\)均为0。
对这个样本,交叉熵(cross entropy)损失为
\[
\begin{aligned}L &= - (y_1 \log \hat{y}_1 + \dots + y_K \log \hat{y}_K) \\&= -y_p \log \hat{y}_p \\ &= - \log \hat{y}_p\end{aligned}
\]
均方误差损失(mean squared error,MSE)为
\[
\begin{aligned}L &= (y_1 - \hat{y}_1)^2 + \dots + (y_K - \hat{y}_K)^2 \\&= (1 - \hat{y}_p)^2 + (\hat{y}_1^2 + \dots + \hat{y}_{p-1}^2 + \hat{y}_{p+1}^2 + \dots + \hat{y}_K^2)\end{aligned}
\]
则\(m\)个样本的损失为
\[
\ell = \frac{1}{m} \sum_{i=1}^m L_i
\]
对比交叉熵损失与均方误差损失,只看单个样本的损失即可,下面从两个角度进行分析。
损失函数角度
损失函数是网络学习的指挥棒,它引导着网络学习的方向——能让损失函数变小的参数就是好参数。
所以,损失函数的选择和设计要能表达你希望模型具有的性质与倾向。
对比交叉熵和均方误差损失,可以发现,两者均在\(\hat{y} = y = 1\)时取得最小值0,但在实践中\(\hat{y}_p\)只会趋近于1而不是恰好等于1,在\(\hat{y}_p < 1\)的情况下,
- 交叉熵只与label类别有关,\(\hat{y}_p\)越趋近于1越好
- 均方误差不仅与\(\hat{y}_p\)有关,还与其他项有关,它希望\(\hat{y}_1, \dots, \hat{y}_{p-1}, \hat{y}_{p+1}, \dots, \hat{y}_K\)越平均越好,即在\(\frac{1-\hat{y}_p}{K-1}\)时取得最小值
分类问题中,对于类别之间的相关性,我们缺乏先验。
虽然我们知道,与“狗”相比,“猫”和“老虎”之间的相似度更高,但是这种关系在样本标记之初是难以量化的,所以label都是one hot。
在这个前提下,均方误差损失可能会给出错误的指示,比如猫、老虎、狗的3分类问题,label为\([1, 0, 0]\),在均方误差看来,预测为\([0.8, 0.1, 0.1]\)要比\([0.8, 0.15, 0.05]\)要好,即认为平均总比有倾向性要好,但这有悖我们的常识。
而对交叉熵损失,既然类别间复杂的相似度矩阵是难以量化的,索性只能关注样本所属的类别,只要\(\hat{y}_p\)越接近于1就好,这显示是更合理的。
softmax反向传播角度
softmax的作用是将\((-\infty, +\infty)\)的几个实数映射到\((0,1)\)之间且之和为1,以获得某种概率解释。
令softmax函数的输入为\(z\),输出为\(\hat{y}\),对结点\(p\)有,
\[
\hat{y}_p = \frac{e^{z_p}}{\sum_{k=1}^K e^{z_k}}
\]
\(\hat{y}_p\)不仅与\(z_p\)有关,还与\(\{z_k | k\neq p\}\)有关,这里仅看$z_p $,则有
\[
\frac{\partial \hat{y}_p}{\partial z_p} = \hat{y}_p(1-\hat{y}_p)
\]
\(\hat{y}_p\)为正确分类的概率,为0时表示分类完全错误,越接近于1表示越正确。根据链式法则,按理来讲,对与\(z_p\)相连的权重,损失函数的偏导会含有\(\hat{y}_p(1-\hat{y}_p)\)这一因子项,\(\hat{y}_p = 0\)时分类错误,但偏导为0,权重不会更新,这显然不对——分类越错误越需要对权重进行更新。
对交叉熵损失,
\[
\frac{\partial L}{\partial \hat{y}_p} = -\frac{1}{\hat{y}_p}
\]
则有
\[
\frac{\partial L}{\partial \hat{z}_p} = \frac{\partial L}{\partial \hat{y}_p} \cdot \frac{\partial \hat{y}_p}{\partial z_p} = \hat{y}_p - 1
\]
恰好将\(\hat{y}_p(1-\hat{y}_p)\)中的\(\hat{y}_p\)消掉,避免了上述情形的发生,且\(\hat{y}_p\)越接近于1,偏导越接近于0,即分类越正确越不需要更新权重,这与我们的期望相符。
而对均方误差损失,
\[
\frac{\partial L}{\partial \hat{y}_p} = -2(1-\hat{y}_p)=2(\hat{y}_p - 1)
\]
则有,
\[
\frac{\partial L}{\partial \hat{z}_p} = \frac{\partial L}{\partial \hat{y}_p} \cdot \frac{\partial \hat{y}_p}{\partial z_p} = -2 \hat{y}_p (1 - \hat{y}_p)^2
\]
显然,仍会发生上面所说的情况——\(\hat{y}_p = 0\),分类错误,但不更新权重。
综上,对分类问题而言,无论从损失函数角度还是softmax反向传播角度,交叉熵都比均方误差要好。
参考
- Loss Functions
- Why You Should Use Cross-Entropy Error Instead Of Classification Error Or Mean Squared Error For Neural Network Classifier Training
加载全部内容
 爱之家商城
爱之家商城 氢松练
氢松练 Face甜美相机
Face甜美相机 花汇通
花汇通 走路宝正式版
走路宝正式版 天天运动有宝
天天运动有宝 深圳plus
深圳plus 热门免费小说
热门免费小说