[NLP] Adaptive Softmax
listenviolet 人气:71. Overview
Adaptive softmax算法在链接1中的论文中提出,该算法目的是为了提高softmax函数的运算效率,适用于一些具有非常大词汇量的神经网络。
在NLP的大部分任务中,都会用到softmax,但是对于词汇量非常大的任务,每次进行完全的softmax会有非常大的计算量,很耗时(每次预测一个token都需要O(|V|)的时间复杂度)。
所以paper中提出adaptive softmax来提升softmax的运算效率。
1) 该算法的提出利用到了单词分布不均衡的特点(unbalanced word distribution)来形成clusters, 这样在计算softmax时可以避免对词汇量大小的线性依赖关系,降低计算时间;
2) 另外通过结合现代架构和矩阵乘积操作的特点,通过使其更适合GPU单元的方式进一步加速计算。
2. Introduction
2.1 一般降低softmax计算复杂度的两种方式
1) 考虑原始分布:近似原始概率分布或近似原始概率分布的子集
2) 构造近似模型,但是产生准确的概率分布。比如:hierarchical softmax.
(上述两个方法可以大致区分为:一是准确的模型产生近似概率分布,二是用近似模型产生准确的概率分布)
2.2 本文贡献点
paper中主要采用的上述(2)的方式,主要借鉴的是hierarchical softmax和一些变型。与以往工作的不同在于,本paper结合了GPU的特点进行了计算加速。主要
1. 定义了一种可以生成 近似层次模型 的策略,该策略同时考虑了矩阵乘积运算的计算时间。这个计算时间并非与矩阵的维数是简单线性关系。
2. 在近来的GPU上对该模型进行了实证分析。在所提出的优化算法中也包含了对实际计算时间模型的定义。
3. 与一般的softmax相比,有2× 到 10× 的加速。这等价于在同等算力限制下提高了准确度。另外一点非常重要,该paper所提出的这种高效计算的方法与一些通过并行提高效率的方法相比,在给定一定量的training data下,对准确度并没有损失。
3. Adaptive Softmax
3.1 矩阵乘积运算的计算时间模型
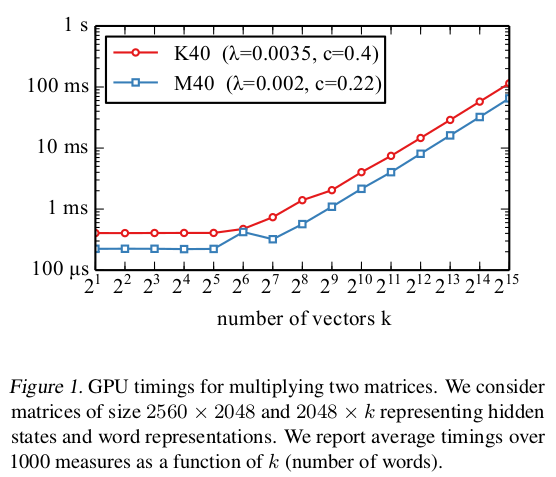
hidden states: (B × d); Word representation: (d × k); 这两个矩阵的乘积运算时间: g(k, B)。其中B是batch size, d: hidden layer 的size, k vectors的数量。
(1) 固定B,d, 探究k值大小与g(k)的关系:
在K40、 M40两种GPU model中进行实验,发现k在大约为$k_0 \approx 50$的范围之内,g(k)是常数级别的,在$k > k_0$后,呈线性依赖关系。其计算模型为:
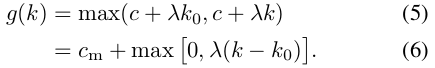
同样的,关于B的计算时间的函数也呈现这样的关系。这可以表示,矩阵相乘时,当其中一个维度很小时,矩阵乘法是低效的。
如何理解呢?比如对于 $k_1 = 2^2$, $k_2 = 2^4$,它们均在同样的常量时间内完成运算,那么显然对于$k1$量级有算力被浪费了。
那么这也说明,一些words的层次结构,其每个节点只具有少量的子节点(比如huffman 编码的tree),是次优的。
(2) 探究batch size B值大小与g(B)的关系:
同样的,当探究计算用时与batch size $B$,的关系时,发现在矩阵乘法运算中,其中一个维度很小时计算并不高效。因此会导致:
(i) 在层次结构中,因为每个节点只有少数一些孩子节点 (比如Huffman 树),其计算效率是次优的;
(ii) 对于按照词频划分clusters后,那些只包含稀有词的cluster,被选择的概率为p, 并且其batch size也缩减为 $p B$,也会出现以上所述的低效的矩阵乘积运算问题。
(3) 本文的计算模型
所以paper中综合考虑了k与B,提出了下面的计算模型:
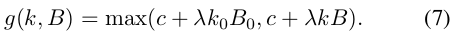
对于Adaptive Softmax, 其核心思想是根据词频大小,将不同词频区间的词分为不同的clusters,按照词频高的优先访问的原则,来对每个cluster整体,进而对cluster中的每个词进行访问,进行softmax操作。
那么paper中首先以2个clusters为例,对该模型进行讲解,之后推广到多个clusters的一般情况。
3.2 Two-Clusters Case
根据Zipf定律,在Penn TreeBank中 20%的词,可以覆盖一般文档中87%的出现过的词。
直观地,可以将字典$V$中的词分为$V_h$、$V_t$两个部分。其中$V_h$表示高频词集合(head),$V_t$表示低频词集合(tail)。一般地,$|V_h| << |V_t|$,$P(V_h) >> P(V_t)$。
(1) Clusters 的组织
直观地可以想到对于这两个clusters有两种组织方式:(i) 两个clusters都是2层的树结构,(ii) 将head部分用一个短列表保存,对tail部分用二层树结构。何种方式更优可以就其计算效率和准确率进行比较:
在准确率方面,(i) 较之 (ii) 一般有 5 ~ 10 %的下降。原因如下:
对于属于cluster $c$的每个词$w$的概率计算为:
若采用(i): $P(c | h) * P(w | c, h)$
若采用(ii): 对于高频词head部分可以直接计算获得 $P(w | h)$,其更为简单直接。
因此,除非(i)(ii)的计算时间有非常大的差别,否则选择(ii)的组织方式。
(2) 对计算时间的缩短

图2. Two clusters示意图
如图2所示,$k_h = |V_h|, k_t = k - k_h, p_t = 1 - p_h$
(i) 对于第一层:对于batch size 为B的输入,在head中对$k_h$个高频词以及1个单位的二层cluster的向量(加阴影部分),共$k_h + 1$个向量,做softmax,
这样占文档中$p_h$的词可以基本确定下来,在head 的 short list 部分找到对应的单词;
而如果与阴影部分进行softmax值更大,表明待预测的词,在第二层的低频词部分;
第一层的计算开销为:$g(k_h + 1, B)$
(ii) 在short list 中确定了 $p_h × B$ 的内容后,还剩下 $p_t B$的输入需要在tail中继续进行softmax来确定所预测的词。
第二层中需要对$k_t$个向量做softmax;
第二层的计算开销为:$g(k_t, pB)$
综上,总的计算开销为:$$C = g(k_h + 1, B) + g(k_t, p_t B)$$
相比于最初的softmax,分母中需要对词典中的每个词的向量逐一进行计算;采用adaptive softmax可以使得该过程分为两部分进行,每部分只需对该部分所包含的词的向量进行计算即可,降低了计算用时。
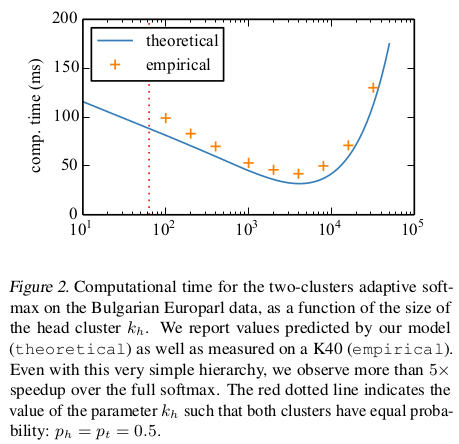
论文中的Figure 2显示了,对于$k_h$的合理划分,最高可以实现相较于完全softmax的5x加速。
(3) 不同cluster的分类器能力不同
由于每个cluster基本是独立计算的,它们并不要求有相同的能力(capacity)。
一般可以为高频词的cluster予以更高的capacity,而可以适当降低词频词的cluster的capacity。因为低频词在文档中很少出现,因此对其capacity的适当降低并不会非常影响总体的性能。
在本文中,采取了为不同的clusters共享隐层,通过加映射矩阵的方式降低分类器的输入大小。一般的,tail部分的映射矩阵将其大小从$d$维缩小到$d_t = d / 4$维。
3.3 一般性情况
在3.2中以分为2个cluster为例,介绍了adaptive softmax如何组织并计算的,这里将其拓展为一般情况,即可以分为多个clusters时的处理方式。
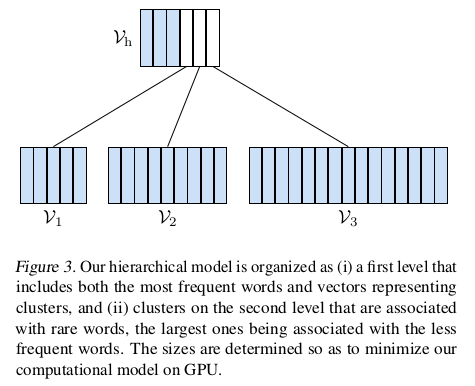
假设将整个词典分为一个head部分和J个词频词cluster部分,那么有:
$$V = V_h \cup V_1 ... V_j, V_i \cap V_j = \phi$$
其中$V_h$在第一层,其余均在第二层,如图Figure 3所示。
每个cluster中的词向量的数目为$k_i = |V_i|$,单词$w$属于某个cluster的概率为:$p_i = \sum_{w \in V_i} p(w)$.
那么,
计算head部分的时间开销为:$C_h = g(J + k_h, B)$
计算每个二层cluster的时间开销为:$\forall_i, C_i = g(k_i, p_i B)$
那么总的时间开销为:$C = g(J + k_h, B) + \sum_i g(k_i, p_i B) \tag8$
回顾公式(7):
$$g(k,B) = max(c + \lambda k_0 B_0, c + \lambda k B) \tag7$$
这里有两部分,一个是常数部分$c + \lambda k_0 B_0$,一个是线性变换部分$c + \lambda k B$。
通过3.1可知,在常数部分GPU的算力并未得到充分利用,因此应尽量避免落入该部分。那么需要满足:
$kB \geq k_0B_0$,这样在求max时,可以利用以上的第二部分。
将(8)式代入(7)的第二部分得:
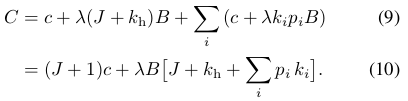
那么接下来的目标就是根据(10) 以最小化时间开销C.
在(10)中,$J ,B$是固定的,那么可以重点关注$\sum_i p_ik_i$与$k_h$。
(1) $\sum_i p_ik_i$
假设$p_{i + j} = p_i + p_j$, 那么 $p_jk_j = (p_{i + j} - p_i) k_j$
$p_ik_i + p_jk_j = p_i(k_i - k_j) + p_{i + j}k_j \tag{11}$
假设$k_i > k_j, p_{i + j}$, $k_j$均固定,那么(11)中只有$p_i$可变,可以通过减小$p_i$的方式使(11)式减小。=> 也即$k_i > k_j$ 且 $p_i$尽量小,即包含越多词的cluster,其概率越小。
(2) $k_h$
减小$k_h$可以使(10)式减小。 => 即为可以使高频词所在的cluster包含更少的词。
综上,给定了cluster的个数J,与batch size B,可以通过给大的cluster分配以更小的概率降低时间开销C.
另外paper中讲到可以用动态规划的方法,在给定了J后,对$k_i$的大小进行划分。
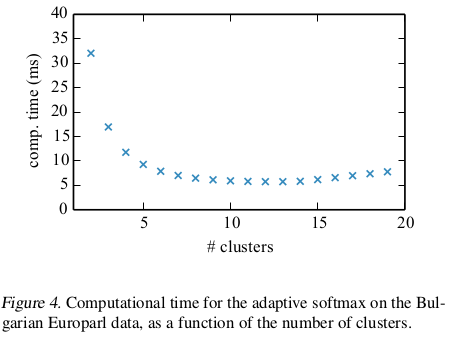
cluster的划分个数$J$。paper中实验了采用不同的J所导致的不同计算时间。如图Figure 4所示。虽然在$10 ~ 15$区间内效果最好,但$ > 5$之后效果没有非常明显的提升。所以文中建议采用2~5个clusters。
实验主要在text8, europarl, one billion word三个数据集上做的,通过比较ppl发现,adaptive softmax仍能保持低的ppl,并且相比于原模型有2x到10x的提速。
参考链接:
1. Efficient softmax approximation for GPUs: https://arxiv.org/pdf/1609.04309.pdf
加载全部内容