博客：blog.shinelee.me | 博客园 | CSDN

权重初始化最佳实践

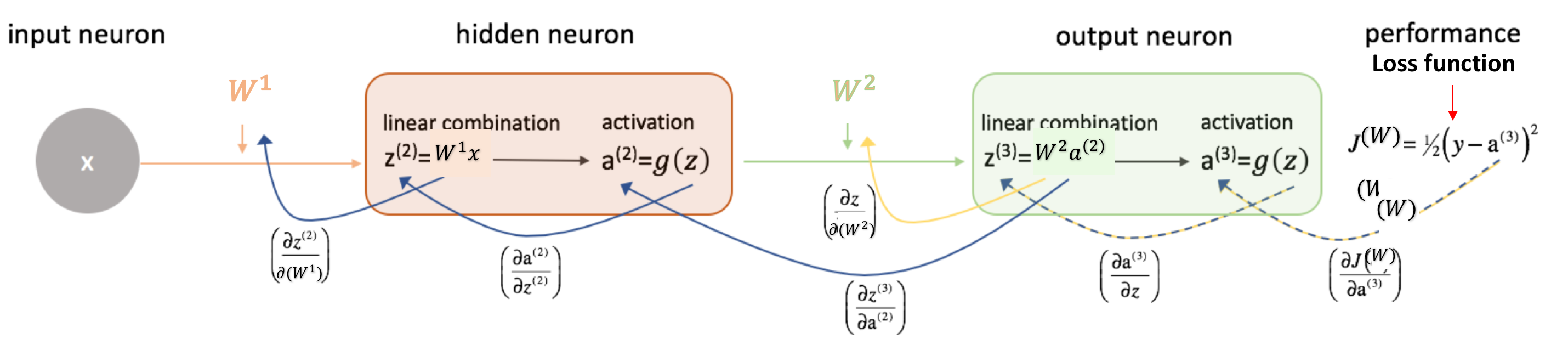
书接上回，全0、常数、过大、过小的权重初始化都是不好的，那我们需要什么样的初始化？

• 因为对权重\(w\)的大小和正负缺乏先验，所以应初始化在0附近，但不能为全0或常数，所以要有一定的随机性，即数学期望\(E(w)=0\)；

• 因为梯度消失和梯度爆炸，权重不易过大或过小，所以要对权重的方差\(Var(w)\)有所控制；

• 深度神经网络的多层结构中，每个激活层的输出对后面的层而言都是输入，所以我们希望不同激活层输出的方差相同，即\(Var(a^{[l]})=Var(a^{[l-1]})\)，这也就意味不同激活层输入的方差相同，即\(Var(z^{[l]})=Var(z^{[l-1]})\)；

• 如果忽略激活函数，前向传播和反向传播可以看成是权重矩阵（转置）的连续相乘。数值太大，前向时可能陷入饱和区，反向时可能梯度爆炸，数值太小，反向时可能梯度消失。所以初始化时，权重的数值范围（方差）应考虑到前向和后向两个过程；

权重的随机初始化过程可以看成是从某个概率分布随机采样的过程，常用的分布有高斯分布、均匀分布等，对权重期望和方差的控制可转化为概率分布的参数控制，权重初始化问题也就变成了概率分布的参数设置问题。

在上回中，我们知道反向传播过程同时受到权重矩阵和激活函数的影响，那么，在激活函数不同以及每层超参数配置不同（输入输出数量）的情况下，权重初始化该做怎样的适配？这里，将各家的研究成果汇总如下，

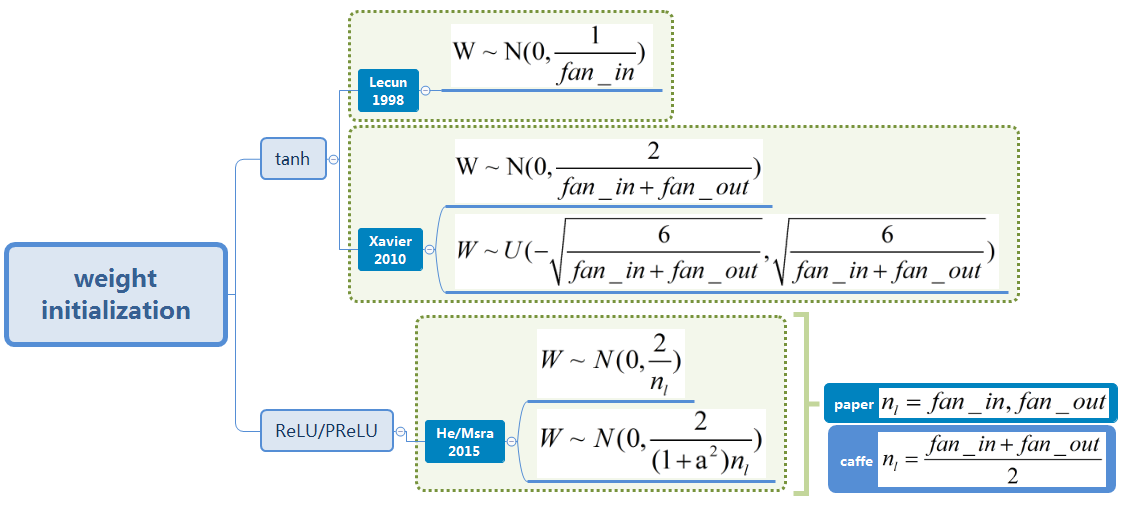
其中，扇入\(fan\_in\)和扇出\(fan\_out\)分别为当前全连接层的输入和输出数量，更准确地说，1个输出神经元与\(fan\_in\)个输入神经元有连接(the number of connections feeding into the node)，1个输入神经元与\(fan\_out\)个输出神经元有连接(the number of connections flowing out of the node)，如下图所示（来自链接），

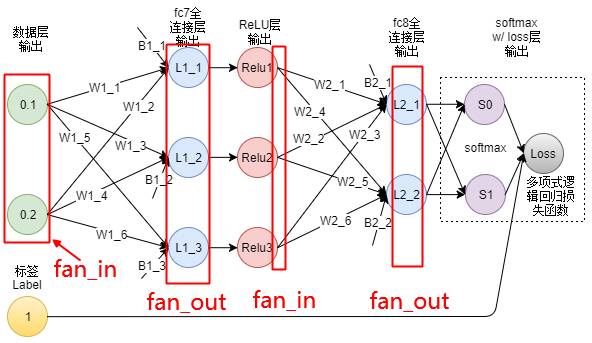
对于卷积层而言，其权重为\(n\)个\(c\times h \times w\)大小的卷积核，则一个输出神经元与\(c\times h \times w\)个输入神经元有连接，即\(fan\_in = c\times h \times w\)，一个输入神经元与\(n\times h \times w\)个输出神经元有连接，即\(fan\_out=n\times h \times w\)。

期望与方差的相关性质

接下来，首先回顾一下期望与方差计算的相关性质。

对于随机变量\(X\)，其方差可通过下式计算，
\[ Var(X) = E(X^2) - (E(X))^2 \]
若两个随机变量\(X\)和\(Y\)，它们相互独立，则其协方差为0，
\[ Cov(X, Y) = 0 \]
进一步可得\(E(XY)=E(X)E(Y)\)，推导如下，
\[ \begin{align} Cov(X, Y) &= E((X-E(X))(Y-E(Y))) \\ &= E(XY)-E(X)E(Y) =0 \end{align} \]
两个独立随机变量和的方差，
\[ \begin{aligned} \operatorname{Var}(X+Y) &=E\left((X+Y)^{2}\right)-(E(X+Y))^{2} \\ &=E\left(X^{2}+Y^{2}+2 X Y\right)-(E(X)+E(Y))^{2} \\ &=\left(E\left(X^{2}\right)+E\left(Y^{2}\right)+2 E(X Y)\right)-\left((E(X))^{2}+(E(Y))^{2}+2 E(X) E(Y)\right) \\ &=\left(E\left(X^{2}\right)+E\left(Y^{2}\right)+2 E(X) E(Y)\right)-\left((E(X))^{2}+(E(Y))^{2}+2 E(X) E(Y)\right) \\ &=E\left(X^{2}\right)-(E(X))^{2}+E\left(Y^{2}\right)-(E(Y))^{2} \\ &=\operatorname{Var}(X)+\operatorname{Var}(Y) \end{aligned} \]
两个独立随机变量积的方差，
\[ \begin{aligned} \operatorname{Var}(X Y) &=E\left((X Y)^{2}\right)-(E(X Y))^{2} \\ &=E\left(X^{2}\right) E\left(Y^{2}\right)-(E(X) E(Y))^{2} \\ &=\left(\operatorname{Var}(X)+(E(X))^{2}\right)\left(\operatorname{Var}(Y)+(E(Y))^{2}\right)-(E(X))^{2}(E(Y))^{2} \\ &=\operatorname{Var}(X) \operatorname{Var}(Y)+(E(X))^{2} \operatorname{Var}(Y)+\operatorname{Var}(X)(E(Y))^{2} \end{aligned} \]

全连接层方差分析

对线性组合层+非线性激活层，计算如下所示，其中\(z_i^{[l-1]}\)为\(l-1\)层第\(i\)个激活函数的输入，\(a_i^{[l-1]}\)为其输出，\(w_{ij}^{[l]}\)为第\(l\)层第\(i\)个输出神经元与第\(j\)个输入神经元连接的权重，\(b^{[l]}\)为偏置，计算方式如下
\[ \begin{align}a_i^{[l-1]} &= f(z_i^{[l-1]}) \\z_i^{[l]} &= \sum_{j=1}^{fan\_in} w_{ij}^{[l]} \ a_j^{[l-1]}+b^{[l]} \\a_i^{[l]} &= f(z_i^{[l]})\end{align} \]
在初始化阶段，将每个权重以及每个输入视为随机变量，可做如下假设和推断，

• 网络输入的每个元素\(x_1, x_2, \dots\)为独立同分布；
• 每层的权重随机初始化，同层的权重$w_{i1}, w_{i2}, \dots \(**独立同分布**，且期望\)E(w)=0$；
• 每层的权重\(w\)和输入\(a\)随机初始化且相互独立，所以两者之积构成的随机变量\(w_{i1}a_1, w_{i2}a_2, \dots\)亦相互独立，且同分布；
• 根据上面的计算公式，同层的\(z_1, z_2, \dots\)为独立同分布，同层的\(a_1, a_2, \dots\)也为独立同分布；

需要注意的是，上面独立同分布的假设仅在初始化阶段成立，当网络开始训练，根据反向传播公式，权重更新后不再相互独立。

在初始化阶段，输入\(a\)与输出\(z\)方差间的关系如下，令\(b=0\)，
\[ \begin{align} Var(z) &=Var(\sum_{j=1}^{fan\_in} w_{ij} \ a_j) \\ &= fan\_in \times (Var(wa)) \\ &= fan\_in \times (Var(w) \ Var(a) + E(w)^2 Var(a) + Var(w) E(a)^2) \\ &= fan\_in \times (Var(w) \ Var(a) + Var(w) E(a)^2) \end{align} \]

tanh下的初始化方法

若激活函数为线性恒等映射，即\(f(x)=x\)，则\(a = z\)，自然\(E(a)=E(z)\)，\(Var(a) = Var(z)\)。

因为网络输入的期望\(E(x)=0\)，每层权重的期望\(E(w) = 0\)，在前面相互独立的假设下，根据公式\(E(XY)=E(X)E(Y)\)，可知\(E(a)=E(z)=\sum E(wa)=\sum E(w)E(a)=0\)。由此可得，
\[ Var(a^{[l]}) = Var(z^{[l]}) = fan\_in \times Var(w) \times Var(a^{[l-1]}) \]
更进一步地，令\(n^{[l]}\)为第\(l\)层的输出数量（\(fan\_out\)），则第\(l\)层的输入数量（$fan_in \(）即前一层的输出数量为\)n^{[l-1]}\(。第\)L$层输出的方差为
\[ \begin{align} Var(a^{L}) = Var(z^{[L]}) &= n^{[L-1]} Var(w^{[L]}) Var(a^{[L-1]}) \\ &=\left[\prod_{l=1}^{L} n^{[l-1]} Var(w^{[l]})\right] {Var}(x) \end{align} \]
反向传播时，需要将上式中的\(n^{[l-1]}\)替换为\(n^{[l]}\)（即\(fan\_in\)替换为\(fan\_out\)），同时将\(x\)替换为损失函数对网络输出的偏导。

所以，经过\(t\)层，前向传播和反向传播的方差，将分别放大或缩小
\[ \prod^{t} n^{[l-1]} Var(w^{[l]}) \\ \prod^{t} n^{[l]} Var(w^{[l]}) \]
为了避免梯度消失和梯度爆炸，最好保持这个系数为1。

需要注意的是，上面的结论是在激活函数为恒等映射的条件下得出的，而tanh激活函数在0附近可近似为恒等映射，即$tanh(x) \approx x $。

Lecun 1998

Lecun 1998年的paper Efficient BackProp ，在输入Standardization以及采用tanh激活函数的情况下，令\(n^{[l-1]}Var(w^{[l]})=1\)，即在初始化阶段让前向传播过程每层方差保持不变，权重从如下高斯分布采样，其中第\(l\)层的\(fan\_in = n^{[l-1]}\)，
\[ W \sim N(0, \frac{1}{fan\_in}) \]

Xavier 2010

在paper Xavier-2010-Understanding the difficulty of training deep feedforward neural networks中，Xavier和Bengio同时考虑了前向过程和反向过程，使用\(fan\_in\)和\(fan\_out\)的平均数对方差进行归一化，权重从如下高斯分布中采样，
\[ W \sim N(0, \frac{2}{fan\_in + fan\_out}) \]
同时文章中还提及了从均匀分布中初始化的方法，因为均匀分布的方差与分布范围的关系为
\[ Var(U(-n, n)) = \frac{n^2}{3} \]
若令\(Var(U(-n, n)) = \frac{2}{fan\_in + fan\_out}\)，则有
\[ n = \frac{\sqrt{6}}{\sqrt{fan\_in + fan\_out}} \]
即权重也可从如下均匀分布中采样，
\[ W \sim U(-\frac{\sqrt{6}}{\sqrt{fan\_in + fan\_out}}, \frac{\sqrt{6}}{\sqrt{fan\_in + fan\_out}}) \]
在使用不同激活函数的情况下，是否使用Xavier初始化方法对test error的影响如下所示，图例中带\(N\)的表示使用Xavier初始化方法，Softsign一种为类tanh但是改善了饱和区的激活函数，图中可以明显看到tanh 和tanh N在test error上的差异。

论文还有更多训练过程中的权重和梯度对比图示，这里不再贴出，具体可以参见论文。

ReLU/PReLU下的初始化方法

搬运一下上面的公式，
\[ Var(z)= fan\_in \times (Var(w) \ Var(a) + Var(w) E(a)^2) \]
因为激活函数tanh在0附近可近似为恒等映射，所以在初始化阶段可以认为\(E(a) = 0\)，但是对于ReLU激活函数，其输出均大于等于0，不存在负数，所以\(E(a) = 0\)的假设不再成立。

但是，我们可以进一步推导得到，
\[ \begin{align} Var(z) &= fan\_in \times (Var(w) \ Var(a) + Var(w) E(a)^2) \\ &= fan\_in \times (Var(w) (E(a^2) - E(a)^2)+Var(w)E(a)^2) \\ &= fan\_in \times Var(w) \times E(a^2) \end{align} \]

He 2015 for ReLU

对于某个具体的层\(l\)则有，
\[ Var(z^{[l]}) = fan\_in \times Var(w^{[l]}) \times E((a^{[l-1]})^2) \]
如果假定\(w{[l-1]}\)来自某个关于原点对称的分布，因为\(E(w^{[l-1]}) = 0\)，且\(b^{[l-1]} = 0\)，则可以认为\(z^{[l-1]}\)分布的期望为0，且关于原点0对称。

对于一个关于原点0对称的分布，经过ReLU后，仅保留大于0的部分，则有
\[ \begin{align}Var(x) &= \int_{-\infty}^{+\infty}(x-0)^2 p(x) dx \\&= 2 \int_{0}^{+\infty}x^2 p(x) dx \\&= 2 E(\max(0, x)^2)\end{align} \]
所以，上式可进一步得出，
\[ \begin {align}Var(z^{[l]}) &= fan\_in \times Var(w^{[l]}) \times E((a^{[l-1]})^2) \\&= \frac{1}{2} \times fan\_in \times Var(w^{[l]}) \times Var(z^{[l-1]}) \end{align} \]
类似地，需要放缩系数为1，即
\[ \frac{1}{2} \times fan\_in \times Var(w^{[l]}) = 1 \\ Var(w) = \frac{2}{fan\_in} \]
即从前向传播考虑，每层的权重初始化为
\[ W \sim N(0, \frac{2}{fan\_in}) \]
同理，从后向传播考虑，每层的权重初始化为
\[ W \sim N(0, \frac{2}{fan\_out}) \]
文中提到，单独使用上面两个中的哪一个都可以，因为当网络结构确定之后，两者对方差的放缩系数之比为常数，即每层扇入扇出之比的连乘，解释如下，

使用Xavier和He初始化，在激活函数为ReLU的情况下，test error下降对比如下，22层的网络，He的初始化下降更快，30层的网络，Xavier不下降，但是He正常下降。

He 2015 for PReLU

对于PReLU激活函数，负向部分为\(f(x) = ax\)，如下右所示，

对于PReLU，求取\(E((a^{[l-1]})^2)\)可对正向和负向部分分别积分，不难得出，
\[ \frac{1}{2} (1 + a^2) \times fan\_in \times Var(w^{[l]}) = 1 \\Var(w) = \frac{2}{(1 + a^2) fan\_in} \\W \sim N(0, \frac{2}{(1 + a^2) fan\_in}) \\W \sim N(0, \frac{2}{(1 + a^2) fan\_out}) \]

caffe中的实现

尽管He在paper中说单独使用\(fan\_in\)或\(fan\_out\)哪个都可以，但是，在Caffe的实现中，还是提供了两者平均值的方式，如下所示，当然默认是使用\(fan\_in\)。

小结

至此，对深度神经网络权重初始化方法的介绍已告一段落。虽然因为BN层的提出，权重初始化可能已不再那么紧要。但是，对经典权重初始化方法经过一番剖析后，相信对神经网络运行机制的理解也会更加深刻。

以上。

参考

• cs231n-Neural Networks Part 2: Setting up the Data and the Loss
• paper-Efficient BackProp
• paper-Understanding the difficulty of training deep feedforward neural networks
• paper-Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification
• wiki-Variance
• Initializing neural networks
• Weight Initialization in Neural Networks: A Journey From the Basics to Kaiming
• Kaiming He initialization
• Choosing Weights: Small Changes, Big Differences
• Understand Kaiming Initialization and Implementation Detail in PyTorch