【algo&ds】【吐血整理】4.树和二叉树、完全二叉树、满二叉树、二叉查找树、平衡二叉树、堆、哈夫曼树、B树、字典树、红黑树、跳表、散列表
ericling 人气:5本博客内容耗时4天整理,如果需要转载,请注明出处,谢谢。
1.树
1.1树的定义
在计算机科学中,树(英语:tree)是一种抽象数据类型(ADT)或是实作这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由n(n>0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
- 每个节点都只有有限个子节点或无子节点;
- 没有父节点的节点称为根节点;
- 每一个非根节点有且只有一个父节点;
- 除了根节点外,每个子节点可以分为多个不相交的子树;
- 树里面没有环路(cycle)

1.2常见术语
- 节点的度:一个节点含有的子树的个数称为该节点的度;
- 树的度:一棵树中,最大的节点度称为树的度;
- 叶节点或终端节点:度为零的节点;
- 非终端节点或分支节点:度不为零的节点;
- 父亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
- 兄弟节点:具有相同父节点的节点互称为兄弟节点;
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0;
- 高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0;
- 堂兄弟节点:父节点在同一层的节点互为堂兄弟;
- 节点的祖先:从根到该节点所经分支上的所有节点;
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
- 森林:由m(m>=0)棵互不相交的树的集合称为森林;
1.3树的种类
无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树;
有序树:树中任意节点的子节点之间有顺序关系,这种树称为有序树;
二叉树
:每个节点最多含有两个子树的树称为二叉树;
完全二叉树
:对于一颗二叉树,假设其深度为d(d>1)。除了第d层外,其它各层的节点数目均已达最大值,且第d层所有节点从左向右连续地紧密排列,这样的二叉树被称为完全二叉树;
- 满二叉树:所有叶节点都在最底层的完全二叉树;
平衡二叉树(AVL树):当且仅当任何节点的两棵子树的高度差不大于1的二叉树;
排序二叉树(二叉查找树(英语:Binary Search Tree)):也称二叉搜索树、有序二叉树;
霍夫曼树:带权路径最短的二叉树称为哈夫曼树或最优二叉树;
B树:一种对读写操作进行优化的自平衡的二叉查找树,能够保持数据有序,拥有多于两个子树。
1.4树的存储结构
1.儿子-兄弟表示法

2.还有一种静态写法,数据域保留,指针域存放其所有子节点的地址(比如开一个数组,存放所有子节点的地址,有点类似于静态链表)
struct node{
typename data;//数据域
vector child;//指针域
}Node[maxn];其对应的创建节点函数如下:
int index = 0;
int newNode(int v){
Node[index].data = v;
Node[index].child.clear();
return index++;
}2.二叉树

2.1二叉树的性质
性质1
在二叉树的第i层上至多有2^(i-1)个结点(i>0)
因为一个节点度不大于2(即每个结点只能有两棵子树),如果假设这棵二叉树是一棵满二叉树,那么每个结点都有两棵子树,按每层来看的话,会发现它是首项为1,公比为2的等比数列,所以第i层最多有2^(i-1)个结点(i>0)
性质2
一棵深度为k的二叉树中,最多有2^k-1个结点
根据性质一,通过等比数列前N项和展开就可以证明出来。
性质3
具有n个结点的完全二叉树的深度k为[log2n]+1
log2n是以2为底,markdown语法只会几个常用的,将就着看。
性质4
对于一棵非空的二叉树,如果叶子结点数为n0,度为2的结点数为n2,
则n0 = n2+1
整棵树的结点数: n = n0+n1+n2 (n0叶子结点数,n1度为1的结点数,n2度为2的结点数)
根据节点度的定义子结点的的数量为: n0×0+n1×1+n2×2
子节点的数量为:n-1 (除根以外每个结点都是子节点)
即n-1 = n0×0+n1×1+n2×2 = n0+n1+n2-1
所以解得 n0 = n2+1
性质5
对于具有n个节点的完全二叉树,如果按照从上至下和从左至右的顺序对二叉树中所有结点进行从1的编号,则对于任意的序号为i结点,有:
- 如果i>1,则序号为i的结点的双亲结点为i/2,如果i==1,则序号为i的结点是根节点,无双亲结点
- 如果
2*i<=n,则序号为i的结点的左孩子节点的序号为2*i,否则i结点无左孩子 - 如果
2*i+1<=n,则序号为i的结点的右孩子节点的序号为2*i+1,否则i结点无右孩子
注意:性质1,2,4所有二叉树都通用,性质3,5只有完全二叉树适用

2.2完全二叉树
对于一颗二叉树,假设其深度为d(d>1)。除了第d层外,其它各层的节点数目均已达最大值,且第d层所有节点从左向右连续地紧密排列,这样的二叉树被称为完全二叉树。

1.二叉树的顺序存储结构
因为完全二叉树的这种特性,所以它也可以使用数组这种连续存储结构来实现。具体地说,如果对完全二叉树当中的任何一个节点(设编号为x),其左孩子的编号一定是2x,而右孩子的编号一定是2x+1。也就是说,可以通过建立一个大小为2^k(k为完全二叉树的最大高度)的数组来存放所有节点的信息,这样做的好处是,可以直接用数组的下标来获取指定序号的节点数据,并且可以直接计算得到左右孩子的编号。

除此之外,该数组中元素存放的顺序恰好为该完全二叉树的层序遍历序列。而判断某个节点是否为叶子节点的标志为:该节点(记下标为root)的左子节点的编号root*2大于节点总个数n
如上图举例,4为叶子节点,它的左孩子节点为2*4=8>节点总个数7
2不是叶子节点2*2=4<7
当然非完全二叉树(也就是一般的二叉树)也可以这样使用顺序存储结构来实现,但是会造成空间浪费。原理就是把空的节点补全(数据域都为空),使得一个一般二叉树变成对应的完全二叉树。

所以一般二叉树更多地使用链表来实现。
2.二叉树的链表存储结构
一般来说,二叉树采用链表来定义,和普通链表的区别是,由于二叉树每个节点有两条出边,因此指针域变成了两个——分别指向左子树根节点地址和右子树根节点地址。如果某个子树不存在,则指向NULL。其定义方式如下:
struct node{
typename data; //数据域
node* lchild; //指向左子树根节点的地址
node* rchild; //指向右子树根节点的地址
}对应的存储结构图示如下:

由于在二叉树建树前根节点不存在,因此其地址一般设置为NULL
node* root = NULL;新建节点的代码实现如下:
node* newNode(int v){
node* Node = new node;//申请一个node型变量的地址空间
Node->data = v; //节点数据域
Node->lchild = Node->rchild =NULL;
return Node;
}2.3二叉树的四种遍历方式
二叉树的遍历是指通过一定顺序访问二叉树的所有结点。遍历方法一般有四种:先序遍历、中序遍历、后序遍历及层次遍历。
其中,前三种一般使用深度优先搜索(DFS)实现,而层次遍历一般用广度优先搜索(BFS)实现。
把一颗二叉树分成三个部分,根节点、左子树、右子树,且对左子树和右子树同样进行这样的划分,这样对树的遍历就可以分解为对这三部分的遍历。无论是这三种遍历中的哪一种,左子树一定先于右子树遍历,且所谓的“先中后”都是指根结点root在遍历中的位置,因此先序遍历的访问顺序是根结点→左子树→右子树,中序遍历的访问顺序是左子树→根结点→右子树,后序遍历的访问顺序是左子树→右子树→根结点。
层次遍历,是把二叉树从第一层(也就是根节点)开始遍历,每一层从左到右遍历完,然后遍历下一层,直到所有节点都访问完。
1.先序遍历

递归实现
void PreorderTraversal( BinTree BT )
{
if( BT ) {
printf("%d ", BT->Data );
PreorderTraversal( BT->Left );
PreorderTraversal( BT->Right );
}
}非递归实现
void PreorderTraversal( BinTree BT ) {
BinTree T = BT;
Stack S = CreatStack( MaxSize ); /*创建并初始化堆栈S*/
while( T || !IsEmpty(S) ) {
while(T) { /*一直向左并将沿途结点压入堆栈*/
Push(S,T);
printf("%5d", T->Data); /*(访问)打印结点*/
T = T->Left;
}
if(!IsEmpty(S)) {
T = Pop(S); /*结点弹出堆栈*/
T = T->Right; /*转向右子树*/
}
}
}由于先序遍历先访问根节点,因此对一棵二叉树的先序遍历序列,序列的第一个一定是根节点。
2.中序遍历

递归实现
void InorderTraversal( BinTree BT )
{
if( BT ) {
InorderTraversal( BT->Left );
/* 此处假设对BT结点的访问就是打印数据 */
printf("%d ", BT->Data); /* 假设数据为整型 */
InorderTraversal( BT->Right );
}
}非递归实现思路
- 遇到一个结点,就把它压栈,并去遍历它的左子树;
- 当左子树遍历结束后,从栈顶弹出这个结点并访问它;
- 然后按其右指针再去中序遍历该结点的右子树。
void InorderTraversal( BinTree BT ) {
BinTree T = BT;
Stack S = CreatStack( MaxSize ); /*创建并初始化堆栈S*/
while( T || !IsEmpty(S) ) {
while(T) { /*一直向左并将沿途结点压入堆栈*/
Push(S,T);
T = T->Left;
}
if(!IsEmpty(S)) {
T = Pop(S); /*结点弹出堆栈*/
printf("%5d", T->Data); /*(访问)打印结点*/
T = T->Right; /*转向右子树*/
}
}
}由于中序遍历总是把根节点放在左子树和右子树中间,因此只要知道根节点,就可以通过根节点在中序遍历序列中的位置区分出左子树和右子树。
3.后序遍历

递归实现
void PostorderTraversal( BinTree BT )
{
if( BT ) {
PostorderTraversal( BT->Left );
PostorderTraversal( BT->Right );
printf("%d ", BT->Data);
}
}非递归实现
void PostOrderTraversal(Bintree BT) {
Bintree T = BT;
Bintree LT = NULL;
Stack S = CreateStack(Maxsize);
while (T || !IsEmpty(S)) {
while (T) {
Push(S, T);
T = T->left; //转向左子树
}
if (!IsEmpty(S)) {
T = Pop(s);
if ((T-> Right== NULL)||(T->Right == LT)) { //判断右节点为空或者右节点已经输出
printf("%d", T->Data);
LT = T; //记录下上一个被输出的
T = NULL;
} else {
Push(S, T); //第二次入栈(相当于T没有出栈)
T = T->Right; //转向右子树
}
}
}
}后序遍历总是把根节点放在最后访问,这和先序遍历恰好相反,因此对于后序遍历序列来说,序列的最后一个一定是根节点。
4.层序遍历

void LevelorderTraversal ( BinTree BT )
{
Queue Q;
BinTree T;
if ( !BT ) return; /* 若是空树则直接返回 */
Q = CreatQueue(); /* 创建空队列Q */
AddQ( Q, BT );
while ( !IsEmpty(Q) ) {
T = DeleteQ( Q );
printf("%d ", T->Data); /* 访问取出队列的结点 */
if ( T->Left ) AddQ( Q, T->Left );
if ( T->Right ) AddQ( Q, T->Right );
}
}这里的遍历就是采用的广度优先搜索的思想,可以参考另外一篇文章
注意点:队列中的元素是node*型而不是node型。队列中保存的值是原元素的一个副本,也就是说类似于值传递,而不是引用传递,所以通过存地址的方式,来达到联动修改的目的。更多的说明请参考文章
2.4遍历二叉树的应用
1.输出二叉树中的叶子结点。
void PreOrderPrintLeaves( BinTree BT ) {
if( BT ) {
if ( !BT-Left && !BT->Right )
printf(“%d”, BT->Data );
PreOrderPrintLeaves ( BT->Left );
PreOrderPrintLeaves ( BT->Right );
}
}2.求二叉树的高度。
int PostOrderGetHeight( BinTree BT ) {
int HL, HR, MaxH;
if( BT ) {
HL = PostOrderGetHeight(BT->Left); /*求左子树的深度*/
HR = PostOrderGetHeight(BT->Right); /*求右子树的深度*/
MaxH = (HL > HR)? HL : HR; /*取左右子树较大的深度*/
return ( MaxH + 1 ); /*返回树的深度*/
} else return 0; /* 空树深度为0 */
}3.给出中序遍历和先序遍历的序列,构建完整二叉树
- 根据先序遍历序列第一个结点确定根结点;
- 根据根结点在中序遍历序列中分割出左右两个子序列;
- 对左子树和右子树分别递归使用相同的方法继续分解。
BiTNode* CreatBiTree(char *pre,char *in,int n) {
if(n<=0) return NULL;
BiTree bt;
bt=(BiTree)malloc(sizeof(BiTree));
bt->data=pre[0];
char *p=strchr(in,pre[0]);
int len=p-in;
bt->lchild=CreatBiTree(pre+1,in,len);
bt->rchild=CreatBiTree(pre+len+1,p+1,n-len-1);
return bt;
}2.5总结
结论:中序序列可以与先序序列、后序序列、层序序列中的任意一个来构建唯一的二叉树,而后三者两两搭配或是三个一起上都无法构建唯一的二叉树。原因是先序、后序、层序均是提供根节点,作用是相同的,无法唯一确定一颗二叉树,都必须由中序遍历序列来区分出左右子树。
3.二叉查找树
二叉搜索树(BST,Binary Search Tree),也称二叉排序树或二叉查找树。
二叉搜索树:一棵二叉树,可以为空;如果不为空,满足以下性质:
- 非空左子树的所有键值小于其根结点的键值。
- 非空右子树的所有键值大于其根结点的键值。
- 左、右子树都是二叉搜索树。

可以理解为二叉查找树就是顺序存储结构的二分查找的另一种存储结构。
二叉查找树的常见操作集
BinTree Find( ElementType X, BinTree BST )从二叉搜索树BST中查找元素X,返回其所在结点的地址;
算法分析
查找从根结点开始,如果树为空,返回NULL
若搜索树非空,则根结点关键字和X进行比较,并进行不同处理:
若X小于根结点键值,只需在左子树中继续搜索;
如果X大于根结点的键值,在右子树中进行继续搜索;
若两者比较结果是相等,搜索完成,返回指向此结点的指针。递归实现
BinTree Find( ElementType X, BinTree BST ) { if( !BST ) return NULL; /*查找失败*/ if( X > BST->Data ) return Find( X, BST->Right ); /*在右子树中继续查找*/ else if( X < BST->Data ) return Find( X, BST->Left ); /*在左子树中继续查找*/ else /* X == BST->Data */ return BST; /*查找成功,返回结点的找到结点的地址*/ }迭代实现
BinTree IterFind( ElementType X, BinTree BST ) { while( BST ) { if( X > BST->Data ) BST = BST->Right; /*向右子树中移动,继续查找*/ else if( X < BST->Data ) BST = BST->Left; /*向左子树中移动,继续查找*/ else /* X == BST->Data */ return BST; /*查找成功,返回结点的找到结点的地址*/ } return NULL; /*查找失败*/ }查找的效率取决于树的高度,让我联想到了二叉树的最大高度为
log2N(以2为底,N的对数,N为二叉树的总节点个数)。BinTree FindMin( BinTree BST )从二叉搜索树BST中查找并返回最小元素所在结点的地址;
算法分析
最小元素一定是在树的最左分枝的端结点上
递归实现
BinTree FindMin( BinTree BST ) { if( !BST ) return NULL; /*空的二叉搜索树,返回NULL*/ else if( !BST->Left ) return BST; /*找到最左叶结点并返回*/ else return FindMin( BST->Left ); /*沿左分支继续查找*/ }迭代实现
BinTree FindMin( BinTree BST ) { if(BST) while( BST->Left ) BST = BST->Left;/*沿左分支继续查找,直到最左叶结点*/ return BST; }BinTree FindMax( BinTree BST )从二叉搜索树BST中查找并返回最大元素所在结点的地址。
算法分析
最大元素一定是在树的最右分枝的端结点上
递归实现
BinTree FindMax( BinTree BST ) { if( !BST ) return NULL; /*空的二叉搜索树,返回NULL*/ else if( !BST->Right ) return BST; /*找到最右叶结点并返回*/ else return FindMin( BST->Right ); /*沿右分支继续查找*/ }迭代实现
BinTree FindMax( BinTree BST ) { if(BST ) while( BST->Right ) BST = BST->Right;/*沿右分支继续查找,直到最右叶结点*/ return BST; }BinTree Insert( ElementType X, BinTree BST )算法分析
关键是要找到元素应该插入的位置,可以采用与Find类似的方法
递归实现
BinTree Insert( ElementType X, BinTree BST ) { if( !BST ) { /*若原树为空,生成并返回一个结点的二叉搜索树*/ BST = malloc(sizeof(struct TreeNode)); BST->Data = X; BST->Left = BST->Right = NULL; } else /*开始找要插入元素的位置*/ if( X < BST->Data ) BST->Left = Insert( X, BST->Left);/*递归插入左子树*/ else if( X > BST->Data ) BST->Right = Insert( X, BST->Right);/*递归插入右子树*/ /* else X已经存在,什么都不做 */ return BST; }迭代实现
BinTree Insert( ElementType X, BinTree BST ) { while( BST ) { if( X > BST->Data ) BST = BST->Right; /*向右子树中移动,继续查找*/ else if( X < BST->Data ) BST = BST->Left; /*向左子树中移动,继续查找*/ else /* X == BST->Data */ return BST; /*查找成功,返回结点的找到结点的地址*/ } if( !BST ) { BST = malloc(sizeof(struct TreeNode)); BST->Data = X; BST->Left = BST->Right = NULL; } return BST; }BinTree Delete( ElementType X, BinTree BST )算法分析
要考虑三种情况
- 要删除的是叶结点:直接删除,并再修改其父结点指针---置为NULL
- 要删除的结点只有一个孩子结点: 将其父结点的指针指向要删除结点的孩子结点
- 要删除的结点有左、右两棵子树: 用另一结点替代被删除结点:右子树的最小元素 或者 左子树的最大元素
递归实现
BinTree Delete( ElementType X, BinTree BST ) { Position Tmp; if( !BST ) printf("要删除的元素未找到"); else if( X < BST->Data ) BST->Left = Delete( X, BST->Left); /* 左子树递归删除 */ else if( X > BST->Data ) BST->Right = Delete( X, BST->Right); /* 右子树递归删除 */ else /*找到要删除的结点 */ if( BST->Left && BST->Right ) { /*被删除结点有左右两个子结点 */ Tmp = FindMin( BST->Right ); /*在右子树中找最小的元素填充删除结点*/ BST->Data = Tmp->Data; BST->Right = Delete( BST->Data, BST->Right); /*在删除结点的右子树中删除最小元素*/ } else { /*被删除结点有一个或无子结点*/ Tmp = BST; if( !BST->Left ) /* 有右孩子或无子结点*/ BST = BST->Right; else if( !BST->Right ) /*有左孩子或无子结点*/ BST = BST->Left; free( Tmp ); } return BST; }迭代实现
Status Delete(BTreePtr T, ElemType e) { BTreePtr p, pp, minP, minPP, child; child = NULL; p = T; pp = NULL; while ( (p != NULL) && (p->data != e) ) { pp = p; if (e > p->data) { p = p->rchild; } else { p = p->lchild; } } if (p == NULL) return FALSE; //双节点 if ((p->lchild != NULL) && (p->rchild != NULL)) { minPP = p; minP = p->rchild; while (minP->lchild != NULL) { minPP = minP; minP = minP->lchild; } p->data = minP->data; minPP->lchild = minP->rchild; free(minP); return TRUE; } //有一个节点 if ((p->lchild != NULL) || (p->rchild != NULL)) { //应该将原有的pp同child连接在一起 if (p->lchild) { child = p->lchild; } else { child = p->rchild; } if(pp->data>p->data) { pp->lchild=child; } else { pp->rchild=child; } free(p); return TRUE; } //没有节点 if (pp->lchild == p) {//这里面临pp除p以外的节点为null的情况 pp->lchild = child; } else { pp->rchild = child; } return TRUE; }
4.平衡二叉树

平衡因子(Balance Factor,简称BF): BF(T) = hL-hR,其中hL和hR分别为T的左、右子树的高度。
平衡二叉树(Balanced Binary Tree)(AVL树)空树,或者任一结点左、右子树高度差的绝对值不超过1,即|BF(T) |≤ 1
完全二叉树、满二叉树其实都是平衡二叉树,但是非完全二叉树也有可能是平衡二叉树。
比如:

平衡二叉树的调整




typedef struct AVLNode *Position;
typedef Position AVLTree; /* AVL树类型 */
struct AVLNode{
ElementType Data; /* 结点数据 */
AVLTree Left; /* 指向左子树 */
AVLTree Right; /* 指向右子树 */
int Height; /* 树高 */
};
int Max ( int a, int b )
{
return a > b ? a : b;
}
AVLTree SingleLeftRotation ( AVLTree A )
{ /* 注意:A必须有一个左子结点B */
/* 将A与B做左单旋,更新A与B的高度,返回新的根结点B */
AVLTree B = A->Left;
A->Left = B->Right;
B->Right = A;
A->Height = Max( GetHeight(A->Left), GetHeight(A->Right) ) + 1;
B->Height = Max( GetHeight(B->Left), A->Height ) + 1;
return B;
}
AVLTree DoubleLeftRightRotation ( AVLTree A )
{ /* 注意:A必须有一个左子结点B,且B必须有一个右子结点C */
/* 将A、B与C做两次单旋,返回新的根结点C */
/* 将B与C做右单旋,C被返回 */
A->Left = SingleRightRotation(A->Left);
/* 将A与C做左单旋,C被返回 */
return SingleLeftRotation(A);
}
/*************************************/
/* 对称的右单旋与右-左双旋请自己实现 */
/*************************************/
AVLTree Insert( AVLTree T, ElementType X )
{ /* 将X插入AVL树T中,并且返回调整后的AVL树 */
if ( !T ) { /* 若插入空树,则新建包含一个结点的树 */
T = (AVLTree)malloc(sizeof(struct AVLNode));
T->Data = X;
T->Height = 0;
T->Left = T->Right = NULL;
} /* if (插入空树) 结束 */
else if ( X < T->Data ) {
/* 插入T的左子树 */
T->Left = Insert( T->Left, X);
/* 如果需要左旋 */
if ( GetHeight(T->Left)-GetHeight(T->Right) == 2 )
if ( X < T->Left->Data )
T = SingleLeftRotation(T); /* 左单旋 */
else
T = DoubleLeftRightRotation(T); /* 左-右双旋 */
} /* else if (插入左子树) 结束 */
else if ( X > T->Data ) {
/* 插入T的右子树 */
T->Right = Insert( T->Right, X );
/* 如果需要右旋 */
if ( GetHeight(T->Left)-GetHeight(T->Right) == -2 )
if ( X > T->Right->Data )
T = SingleRightRotation(T); /* 右单旋 */
else
T = DoubleRightLeftRotation(T); /* 右-左双旋 */
} /* else if (插入右子树) 结束 */
/* else X == T->Data,无须插入 */
/* 别忘了更新树高 */
T->Height = Max( GetHeight(T->Left), GetHeight(T->Right) ) + 1;
return T;
}平衡二叉查找树不仅满足上面平衡二叉树的定义,还满足二叉查找树的特点。最先被发明的平衡二叉查找树是AVL 树,它严格符合我刚讲到的平衡二叉查找树的定义,即任何节点的左右子树高度相差不超过 1,是一种高度平衡的二叉查找树。
5.堆
堆(英语:Heap)是计算机科学中的一种特别的树状数据结构。若是满足以下特性,即可称为堆:“给定堆中任意节点P和C,若P是C的母节点,那么P的值会小于等于(或大于等于)C的值”。若母节点的值恒小于等于子节点的值,此堆称为最小堆(min heap);反之,若母节点的值恒大于等于子节点的值,此堆称为最大堆(max heap)。在堆中最顶端的那一个节点,称作根节点(root node),根节点本身没有母节点(parent node)。
堆始于J. W. J. Williams在1964年发表的堆排序(heap sort),当时他提出了二叉堆树作为此算法的数据结构。堆在戴克斯特拉算法(英语:Dijkstra's algorithm)中亦为重要的关键。
在队列中,调度程序反复提取队列中第一个作业并运行,因为实际情况中某些时间较短的任务将等待很长时间才能结束,或者某些不短小,但具有重要性的作业,同样应当具有优先权。堆即为解决此类问题设计的一种数据结构。
优先队列(Priority Queue):特殊的“队列”,取出元素的顺序是依照元素的优先权(关键字)大小,而不是元素进入队列的先后顺序。

堆的两个特性
- 结构性:用数组表示的完全二叉树;
- 有序性:任一结点的关键字是其子树所有结点的最大值(或最小值)
- “最大堆(MaxHeap)”,也称“大顶堆”:最大值
- “最小堆(MinHeap)”,也称“小顶堆” :最小值

注意:从根结点到任意结点路径上结点序列的有序性!
5.1堆的抽象数据类型描述
类型名称:最大堆(MaxHeap)
数据对象集:完全二叉树,每个结点的元素值不小于其子结点的元素值
操作集:最大堆H MaxHeap,元素item ElementType,主要操作有:
•MaxHeap Create( int MaxSize ):创建一个空的最大堆。
•Boolean IsFull( MaxHeap H ):判断最大堆H是否已满。
•Insert( MaxHeap H, ElementType item ):将元素item插入最大堆H。
•Boolean IsEmpty( MaxHeap H ):判断最大堆H是否为空。
•ElementType DeleteMax( MaxHeap H ):返回H中最大元素(高优先级)。
5.2最大堆的操作
1.结构体定义
typedef struct HeapStruct *MaxHeap;
struct HeapStruct {
ElementType *Elements; /* 存储堆元素的数组 */
int Size; /* 堆的当前元素个数 */
int Capacity; /* 堆的最大容量 */
};2.最大堆的创建
MaxHeap Create( int MaxSize ) {
/* 创建容量为MaxSize的空的最大堆 */
MaxHeap H = malloc( sizeof( struct HeapStruct ) );
H->Elements = malloc( (MaxSize+1) * sizeof(ElementType));
H->Size = 0;
H->Capacity = MaxSize;
H->Elements[0] = MaxData;
/* 定义“哨兵”为大于堆中所有可能元素的值,便于以后更快操作 */
return H;
}3.最大堆的插入
将新增结点插入到从其父结点到根结点的有序序列中
void Insert( MaxHeap H, ElementType item ) {
/* 将元素item 插入最大堆H,其中H->Elements[0]已经定义为哨兵 */
int i;
if ( IsFull(H) ) {
printf("最大堆已满");
return;
}
i = ++H->Size; /* i指向插入后堆中的最后一个元素的位置 */
for ( ; H->Elements[i/2] < item; i/=2 )/*H->Element[ 0 ] 是哨兵元素,它不小于堆中的最大元素,控制循环结束。*/
H->Elements[i] = H->Elements[i/2]; /* 向下过滤结点 */
H->Elements[i] = item; /* 将item 插入 */
}T (N) = O ( log N )
4.最大堆的删除
ElementType DeleteMax( MaxHeap H ) {
/* 从最大堆H中取出键值为最大的元素,并删除一个结点 */
int Parent, Child;
ElementType MaxItem, temp;
if ( IsEmpty(H) ) {
printf("最大堆已为空");
return;
}
MaxItem = H->Elements[1]; /* 取出根结点最大值 */
/* 用最大堆中最后一个元素从根结点开始向上过滤下层结点 */
temp = H->Elements[H->Size--];
for( Parent=1; Parent*2<=H->Size; Parent=Child ) {
Child = Parent * 2;
if( (Child!= H->Size) &&
(H->Elements[Child] < H->Elements[Child+1]) )
Child++; /* Child指向左右子结点的较大者 */
if( temp >= H->Elements[Child] ) break;
else /* 移动temp元素到下一层 */
H->Elements[Parent] = H->Elements[Child];
}
H->Elements[Parent] = temp;
return MaxItem;
}5.最大堆的建立
建立最大堆:将已经存在的N个元素按最大堆的要求存放在一个一维数组中
方法1:通过插入操作,将N个元素一个个相继插入到一个初始为空的堆中去,其时间代价最大为O(N logN)。
方法2:在线性时间复杂度下建立最大堆。
(1)将N个元素按输入顺序存入,先满足完全二叉树的结构特性
(2)调整各结点位置,以满足最大堆的有序特性。
/*----------- 建造最大堆 -----------*/
void PercDown( MaxHeap H, int p )
{ /* 下滤:将H中以H->Data[p]为根的子堆调整为最大堆 */
int Parent, Child;
ElementType X;
X = H->Data[p]; /* 取出根结点存放的值 */
for( Parent=p; Parent*2<=H->Size; Parent=Child ) {
Child = Parent * 2;
if( (Child!=H->Size) && (H->Data[Child]<H->Data[Child+1]) )
Child++; /* Child指向左右子结点的较大者 */
if( X >= H->Data[Child] ) break; /* 找到了合适位置 */
else /* 下滤X */
H->Data[Parent] = H->Data[Child];
}
H->Data[Parent] = X;
}
void BuildHeap( MaxHeap H )
{ /* 调整H->Data[]中的元素,使满足最大堆的有序性 */
/* 这里假设所有H->Size个元素已经存在H->Data[]中 */
int i;
/* 从最后一个结点的父节点开始,到根结点1 */
for( i = H->Size/2; i>0; i-- )
PercDown( H, i );
}6.哈夫曼树&哈夫曼编码



6.1哈夫曼树的定义
带权路径长度(WPL):设二叉树有n个叶子结点,每个叶子结点带有权值 wk,从根结点到每个叶子结点的长度为 lk,则每个叶子结点的带权路径长度之和就是:

最优二叉树或哈夫曼树: WPL最小的二叉树
6.2构造哈夫曼树
typedef struct TreeNode *HuffmanTree;
struct TreeNode {
int Weight;
HuffmanTree Left, Right;
}
HuffmanTree Huffman( MinHeap H ) {
/* 假设H->Size个权值已经存在H->Elements[]->Weight里 */
int i;
HuffmanTree T;
BuildMinHeap(H); /*将H->Elements[]按权值调整为最小堆*/
for (i = 1; i < H->Size; i++) { /*做H->Size-1次合并*/
T = malloc( sizeof( struct TreeNode) ); /*建立新结点*/
T->Left = DeleteMin(H);
/*从最小堆中删除一个结点,作为新T的左子结点*/
T->Right = DeleteMin(H);
/*从最小堆中删除一个结点,作为新T的右子结点*/
T->Weight = T->Left->Weight+T->Right->Weight;
/*计算新权值*/
Insert( H, T ); /*将新T插入最小堆*/
}
T = DeleteMin(H);
return T;
}6.3哈夫曼树的特点
- 没有度为1的结点;
- 哈夫曼树的任意非叶节点的左右子树交换后仍是哈夫曼树;
- n个叶子结点的哈夫曼树共有2n-1个结点;
对同一组权值{w1 ,w2 , …… , wn},是否存在不同构的两棵哈夫曼树呢?
对一组权值{ 1, 2 , 3, 3 },不同构的两棵哈夫曼树:

6.4哈夫曼编码
给定一段字符串,如何对字符进行编码,可以使得该字符串的编码存储空间最少?
[例] 假设有一段文本,包含58个字符,并由以下7个字符构成:a,e,i,s,t,空格(sp),换行(nl);这7个字符出现的次数不同。如何对这7个字符进行编码,使得总编码空间最少?
【分析】
(1)用等长ASCII编码:58 ×8 = 464位;
(2)用等长3位编码:58 ×3 = 174位;
(3)不等长编码:出现频率高的字符用的编码短些,出现频率低的字符则可以编码长些?


7.B树
B树的应用可以参考另外一篇文章
8.字典树Trie

Trie 树,也叫“字典树”。顾名思义,它是一个树形结构。它是一种专门处理字符串匹配的数据结构,用来解决在一组字符串集合中快速查找某个字符串的问题。它的一个经典应用场景就是输入框的自动提示。
举个例子来说明一下,我们有 6 个字符串,它们分别是:how,hi,her,hello,so,see。我们希望在里面多次查找某个字符串是否存在。如果每次查找,都是拿要查找的字符串跟这 6 个字符串依次进行字符串匹配,那效率就比较低。我们就可以先对这 6 个字符串做一下预处理,组织成 Trie 树的结构,之后每次查找,都是在 Trie 树中进行匹配查找。Trie 树的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起。最后构造出来的就是下面这个图中的样子。

根节点不包含任何信息。每个节点表示一个字符串中的字符,从根节点到红色节点的一条路径表示一个字符串(注意:红色节点并不都是叶子节点)。
Trie树的构造过程如下:


当我们在 Trie 树中查找一个字符串的时候,比如查找字符串“her”,那我们将要查找的字符串分割成单个的字符 h,e,r,然后从 Trie 树的根节点开始匹配。如图所示,绿色的路径就是在 Trie 树中匹配的路径。

如果我们要查找的是字符串“he”呢?我们还用上面同样的方法,从根节点开始,沿着某条路径来匹配,如图所示,绿色的路径,是字符串“he”匹配的路径。但是,路径的最后一个节点“e”并不是红色的。也就是说,“he”是某个字符串的前缀子串,但并不能完全匹配任何字符串。

8.1字典树的存储结构
对于前面的trie树的逻辑存储结构,可以理解为下面这幅图

8.2字典树的代码实现及常用操作
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int Status;
typedef struct Node {
char data;
struct Node *children[26];
Status end;
} Trie, *TriePtr;
void Init(TriePtr *T)
{
(*T) = (TriePtr)malloc(sizeof(Trie));
(*T)->data = '/';
(*T)->end = FALSE;
}
void Insert(TriePtr T, char *str) {
int index;
char c;
while(c = *str++)
{
index = c - 'a';
if (T->children[index] == NULL)
{
TriePtr Node;
Node = (TriePtr)malloc(sizeof(Trie));
Node->data = c;
Node->end = FALSE;
T->children[index] = Node;
}
T = T->children[index];
}
T->end = TRUE;
}
Status Search(TriePtr T, char *str) {
int index;
char c;
while(c = *str++)
{
index = c - 'a';
if (T->children[index] == NULL)
{
return FALSE;
}
T = T->children[index];
}
if (T->end) {
return TRUE;
} else {
return FALSE;
}
}
int main(int argc, char const *argv[])
{
TriePtr T;
Init(&T);
char *str = "hello";
char *str2 = "hi";
Insert(T, str);
printf("str is search %d\n", Search(T, str));
printf("str2 is search %d\n", Search(T, str2));
return 0;
}8.3复杂度分析
时间复杂度
如果要在一组字符串中,频繁地查询某些字符串,用 Trie 树会非常高效。构建 Trie 树的过程,需要扫描所有的字符串,时间复杂度是 O(n)(n 表示所有字符串的长度和)。但是一旦构建成功之后,后续的查询操作会非常高效。每次查询时,如果要查询的字符串长度是 k,那我们只需要比对大约 k 个节点,就能完成查询操作。跟原本那组字符串的长度和个数没有任何关系。所以说,构建好 Trie 树后,在其中查找字符串的时间复杂度是 O(k),k 表示要查找的字符串的长度。
空间复杂度
Trie 树是非常耗内存的,用的是一种空间换时间的思路。
刚刚我们在讲 Trie 树的实现的时候,讲到用数组来存储一个节点的子节点的指针。如果字符串中包含从 a 到 z 这 26 个字符,那每个节点都要存储一个长度为 26 的数组,并且每个数组存储一个 8 字节指针(或者是 4 字节,这个大小跟 CPU、操作系统、编译器等有关)。而且,即便一个节点只有很少的子节点,远小于 26 个,比如 3、4 个,我们也要维护一个长度为 26 的数组。Trie 树的本质是避免重复存储一组字符串的相同前缀子串,但是现在每个字符(对应一个节点)的存储远远大于 1 个字节。按照我们上面举的例子,数组长度为 26,每个元素是 8 字节,那每个节点就会额外需要 26*8=208 个字节。而且这还是只包含 26 个字符的情况。如果字符串中不仅包含小写字母,还包含大写字母、数字、甚至是中文,那需要的存储空间就更多了。所以在某些情况下,Trie 树不一定会节省存储空间。在重复的前缀并不多的情况下,Trie 树不但不能节省内存,还有可能会浪费更多的内存。
8.4Trie树和红黑树、散列表的比较
在刚刚讲的这个场景,在一组字符串中查找字符串,Trie 树实际上表现得并不好。它对要处理的字符串有及其严苛的要求。
- 第一,字符串中包含的字符集不能太大。我们前面讲到,如果字符集太大,那存储空间可能就会浪费很多。即便可以优化,但也要付出牺牲查询、插入效率的代价。
- 第二,要求字符串的前缀重合比较多,不然空间消耗会变大很多。
- 第三,如果要用 Trie 树解决问题,那我们就要自己从零开始实现一个 Trie 树,还要保证没有 bug,这个在工程上是将简单问题复杂化,除非必须,一般不建议这样做。
- 第四,我们知道,通过指针串起来的数据块是不连续的,而 Trie 树中用到了指针,所以,对缓存并不友好,性能上会打个折扣。
综合这几点,针对在一组字符串中查找字符串的问题,我们在工程中,更倾向于用散列表或者红黑树。因为这两种数据结构,我们都不需要自己去实现,直接利用编程语言中提供的现成类库就行了。
9.红黑树
此章节内容都是参考极客时间专栏-《数据结构与算法之美》
9.1红黑树的定义
平衡二叉查找树其实有很多,比如,Splay Tree(伸展树)、Treap(树堆)等,但是我们提到平衡二叉查找树,听到的基本都是红黑树。它的出镜率甚至要高于“平衡二叉查找树”这几个字,有时候,我们甚至默认平衡二叉查找树就是红黑树。
红黑树的英文是“Red-Black Tree”,简称 R-B Tree。它是一种不严格的平衡二叉查找树。顾名思义,红黑树中的节点,一类被标记为黑色,一类被标记为红色。除此之外,一棵红黑树还需要满足这样几个要求:
- 根节点是黑色的;
- 每个叶子节点都是黑色的空节点(NIL),也就是说,叶子节点不存储数据;
- 任何相邻的节点都不能同时为红色,也就是说,红色节点是被黑色节点隔开的;
- 每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点;
这里的第二点要求“叶子节点都是黑色的空节点”,稍微有些奇怪,它主要是为了简化红黑树的代码实现而设置的。它的结构图案例如下,图中去掉了黑色的、空的叶子节点。

为什么说红黑树是“近似平衡”的?
平衡二叉查找树的初衷,是为了解决二叉查找树因为动态更新导致的性能退化问题。所以,“平衡”的意思可以等价为性能不退化。“近似平衡”就等价为性能不会退化的太严重。
二叉查找树很多操作的性能都跟树的高度成正比。一棵极其平衡的二叉树(满二叉树或完全二叉树)的高度大约是 log2n,所以如果要证明红黑树是近似平衡的,我们只需要分析,红黑树的高度是否比较稳定地趋近 log2n 。
接下来一步一步推导红黑树的高度。
首先,我们来看,如果我们将红色节点从红黑树中去掉,那单纯包含黑色节点的红黑树的高度是多少呢?
红色节点删除之后,有些节点就没有父节点了,它们会直接拿这些节点的祖父节点(父节点的父节点)作为父节点。所以,之前的二叉树就变成了四叉树。

前面红黑树的定义里有这么一条:从任意节点到可达的叶子节点的每个路径包含相同数目的黑色节点。我们从四叉树中取出某些节点,放到叶节点位置,四叉树就变成了完全二叉树。所以,仅包含黑色节点的四叉树的高度,比包含相同节点个数的完全二叉树的高度还要小,所以去掉红色节点的“黑树”的高度也不会超过 log2n。
现在把红色节点加回去,高度会变成多少呢?
在红黑树中,红色节点不能相邻,也就是说,有一个红色节点就要至少有一个黑色节点,将它跟其他红色节点隔开。红黑树中包含最多黑色节点的路径不会超过 log2n,所以加入红色节点之后,最长路径不会超过 2log2n,也就是说,红黑树的高度近似 2log2n。所以,红黑树的高度只比高度平衡的 AVL 树的高度(log2n)仅仅大了一倍,在性能上,下降得并不多。这样推导出来的结果不够精确,实际上红黑树的性能更好。
为什么在工程中大家都喜欢用红黑树这种平衡二叉查找树?
前面提到 Treap、Splay Tree,绝大部分情况下,它们操作的效率都很高,但是也无法避免极端情况下时间复杂度的退化。尽管这种情况出现的概率不大,但是对于单次操作时间非常敏感的场景来说,它们并不适用。AVL 树是一种高度平衡的二叉树,所以查找的效率非常高,但是,有利就有弊,AVL 树为了维持这种高度的平衡,就要付出更多的代价。每次插入、删除都要做调整,就比较复杂、耗时。所以,对于有频繁的插入、删除操作的数据集合,使用 AVL 树的代价就有点高了。红黑树只是做到了近似平衡,并不是严格的平衡,所以在维护平衡的成本上,要比 AVL 树要低。所以,红黑树的插入、删除、查找各种操作性能都比较稳定。对于工程应用来说,要面对各种异常情况,为了支撑这种工业级的应用,我们更倾向于这种性能稳定的平衡二叉查找树。
9.2红黑树的实现
红黑树的建立过程会频繁的破坏它的定义中的第三四点,而我们要做的就是把破坏的点恢复过来。在这之前,需要掌握两个非常重要的操作,左旋和右旋,可以参考如下的图片来理解。

1.插入操作的平衡调整
红黑树规定,插入的节点必须是红色的。而且,二叉查找树中新插入的节点都是放在叶子节点上。所以,关于插入操作的平衡调整,有这样两种特殊情况,但是也都非常好处理。
如果插入节点的父节点是黑色的,那我们什么都不用做,它仍然满足红黑树的定义。
如果插入的节点是根节点,那我们直接改变它的颜色,把它变成黑色就可以了。
除此之外,其他情况都会违背红黑树的定义,于是我们就需要进行调整,调整的过程包含两种基础的操作:左右旋转和改变颜色。
红黑树的平衡调整过程是一个迭代的过程。我们把正在处理的节点叫作关注节点。关注节点会随着不停地迭代处理,而不断发生变化。最开始的关注节点就是新插入的节点。新节点插入之后,如果红黑树的平衡被打破,那一般会有下面三种情况。我们只需要根据每种情况的特点,不停地调整,就可以让红黑树继续符合定义,也就是继续保持平衡。我们下面依次来看每种情况的调整过程。提醒你注意下,为了简化描述,我把父节点的兄弟节点叫作叔叔节点,父节点的父节点叫作祖父节点。
1.如果关注节点是 a,它的叔叔节点 d 是红色
- 将关注节点 a 的父节点 b、叔叔节点 d 的颜色都设置成黑色;
- 将关注节点 a 的祖父节点 c 的颜色设置成红色;
- 关注节点变成 a 的祖父节点 c;
- 跳到 CASE 2 或者 CASE 3。

2.如果关注节点是 a,它的叔叔节点 d 是黑色,关注节点 a 是其父节点 b 的右子节点
- 关注节点变成节点 a 的父节点 b;
- 围绕新的关注节点b 左旋;
- 跳到 CASE 3。

3.如果关注节点是 a,它的叔叔节点 d 是黑色,关注节点 a 是其父节点 b 的左子节点
- 围绕关注节点 a 的祖父节点 c 右旋;
- 将关注节点 a 的父节点 b、兄弟节点 c 的颜色互换。
- 调整结束。

2.删除操作的平衡调整
删除操作的平衡调整分为两步,第一步是针对删除节点初步调整。初步调整只是保证整棵红黑树在一个节点删除之后,仍然满足最后一条定义的要求,也就是说,每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点;第二步是针对关注节点进行二次调整,让它满足红黑树的第三条定义,即不存在相邻的两个红色节点。
1. 针对删除节点初步调整
这里需要注意一下,红黑树的定义中“只包含红色节点和黑色节点”,经过初步调整之后,为了保证满足红黑树定义的最后一条要求,有些节点会被标记成两种颜色,“红 - 黑”或者“黑 - 黑”。如果一个节点被标记为了“黑 - 黑”,那在计算黑色节点个数的时候,要算成两个黑色节点。在下面的讲解中,如果一个节点既可以是红色,也可以是黑色,在画图的时候,我会用一半红色一半黑色来表示。如果一个节点是“红 - 黑”或者“黑 - 黑”,我会用左上角的一个小黑点来表示额外的黑色。
CASE 1:如果要删除的节点是 a,它只有一个子节点 b
- 删除节点 a,并且把节点 b 替换到节点 a 的位置,这一部分操作跟普通的二叉查找树的删除操作一样;
- 节点 a 只能是黑色,节点 b 也只能是红色,其他情况均不符合红黑树的定义。这种情况下,我们把节点 b 改为黑色;
- 调整结束,不需要进行二次调整。

CASE 2:如果要删除的节点 a 有两个非空子节点,并且它的后继节点就是节点 a 的右子节点 c
- 如果节点 a 的后继节点就是右子节点 c,那右子节点 c 肯定没有左子树。我们把节点 a 删除,并且将节点 c 替换到节点 a 的位置。这一部分操作跟普通的二叉查找树的删除操作无异;
- 然后把节点 c 的颜色设置为跟节点 a 相同的颜色;
- 如果节点 c 是黑色,为了不违反红黑树的最后一条定义,我们给节点 c 的右子节点 d 多加一个黑色,这个时候节点 d 就成了“红 - 黑”或者“黑 - 黑”;
- 这个时候,关注节点变成了节点 d,第二步的调整操作就会针对关注节点来做。

CASE 3:如果要删除的是节点 a,它有两个非空子节点,并且节点 a 的后继节点不是右子节点
- 找到后继节点 d,并将它删除,删除后继节点 d 的过程参照 CASE 1;
- 将节点 a 替换成后继节点 d;
- 把节点 d 的颜色设置为跟节点 a 相同的颜色;
- 如果节点 d 是黑色,为了不违反红黑树的最后一条定义,我们给节点 d 的右子节点 c 多加一个黑色,这个时候节点 c 就成了“红 - 黑”或者“黑 - 黑”;
- 这个时候,关注节点变成了节点 c,第二步的调整操作就会针对关注节点来做。

2.针对关注节点进行二次调整
经过初步调整之后,关注节点变成了“红 - 黑”或者“黑 - 黑”节点。针对这个关注节点,我们再分四种情况来进行二次调整。二次调整是为了让红黑树中不存在相邻的红色节点。
CASE 1:如果关注节点是 a,它的兄弟节点 c 是红色的
- 围绕关注节点 a 的父节点 b 左旋;
- 关注节点 a 的父节点 b 和祖父节点 c 交换颜色;
- 关注节点不变;
- 继续从四种情况中选择适合的规则来调整。

CASE 2:如果关注节点是 a,它的兄弟节点 c 是黑色的,并且节点 c 的左右子节点 d、e 都是黑色的
- 将关注节点 a 的兄弟节点 c 的颜色变成红色;
- 从关注节点 a 中去掉一个黑色,这个时候节点 a 就是单纯的红色或者黑色;
- 给关注节点 a 的父节点 b 添加一个黑色,这个时候节点 b 就变成了“红 - 黑”或者“黑 - 黑”;
- 关注节点从 a 变成其父节点 b;
- 继续从四种情况中选择符合的规则来调整。

CASE 3:如果关注节点是 a,它的兄弟节点 c 是黑色,c 的左子节点 d 是红色,c 的右子节点 e 是黑色
- 围绕关注节点 a 的兄弟节点 c 右旋;
- 节点 c 和节点 d 交换颜色;
- 关注节点不变;
- 跳转到 CASE 4,继续调整。

CASE 4:如果关注节点 a 的兄弟节点 c 是黑色的,并且 c 的右子节点是红色的
- 围绕关注节点 a 的父节点 b 左旋;
- 将关注节点 a 的兄弟节点 c 的颜色,跟关注节点 a 的父节点 b 设置成相同的颜色;
- 将关注节点 a 的父节点 b 的颜色设置为黑色;
- 从关注节点 a 中去掉一个黑色,节点 a 就变成了单纯的红色或者黑色;
- 将关注节点 a 的叔叔节点 e 设置为黑色;
- 调整结束。

9.3为什么红黑树的定义中,要求叶子节点是黑色的空节点?
之所以有这么奇怪的要求,其实就是为了实现起来方便。只要满足这一条要求,那在任何时刻,红黑树的平衡操作都可以归结为我们刚刚讲的那几种情况。
还是有点不好理解,我通过一个例子来解释一下。假设红黑树的定义中不包含刚刚提到的那一条“叶子节点必须是黑色的空节点”,我们往一棵红黑树中插入一个数据,新插入节点的父节点也是红色的,两个红色的节点相邻,这个时候,红黑树的定义就被破坏了。那我们应该如何调整呢?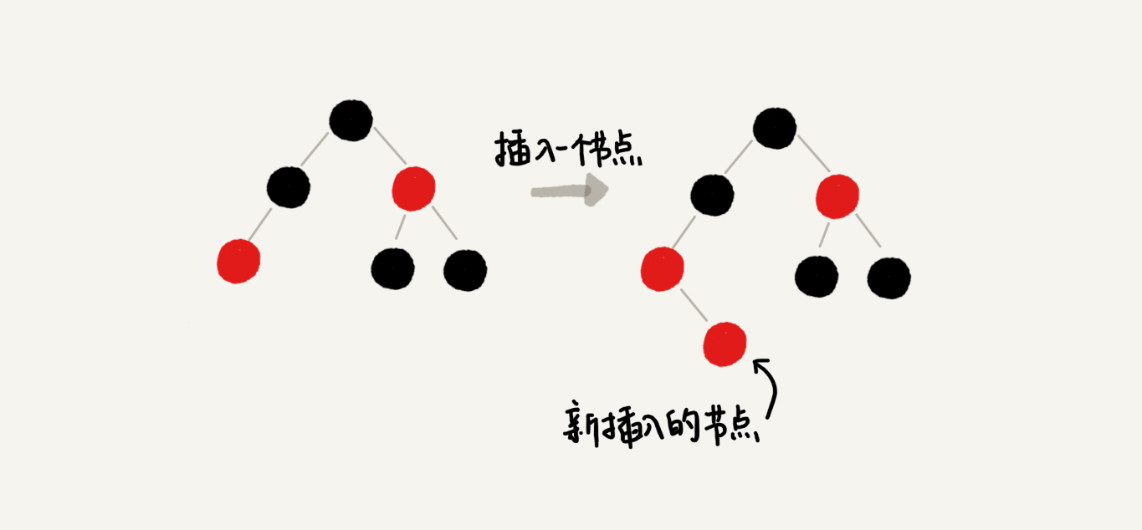
你会发现,这个时候,我们前面讲的插入时,三种情况下的平衡调整规则,没有一种是适用的。但是,如果我们把黑色的空节点都给它加上,变成下面这样,你会发现,它满足 CASE 2 了。
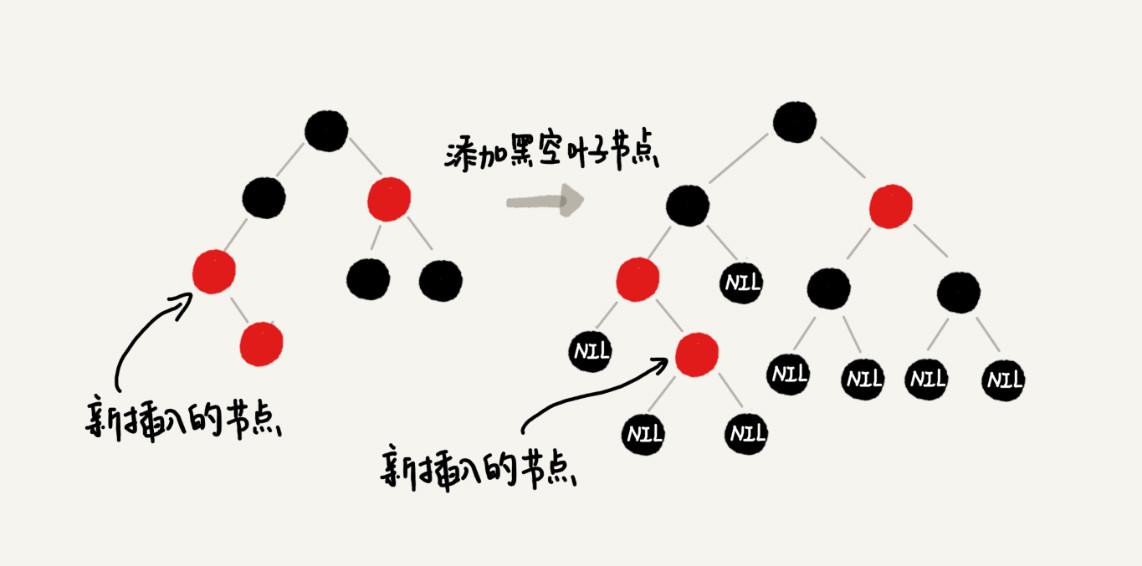
你可能会说,你可以调整一下平衡调整规则啊。比如把 CASE 2 改为“如果关注节点 a 的叔叔节点 b 是黑色或者不存在,a 是父节点的右子节点,就进行某某操作”。当然可以,但是这样的话规则就没有原来简洁了。
你可能还会说,这样给红黑树添加黑色的空的叶子节点,会不会比较浪费存储空间呢?答案是不会的。虽然我们在讲解或者画图的时候,每个黑色的、空的叶子节点都是独立画出来的。实际上,在具体实现的时候,我们只需要像下面这样,共用一个黑色的、空的叶子节点就行了。
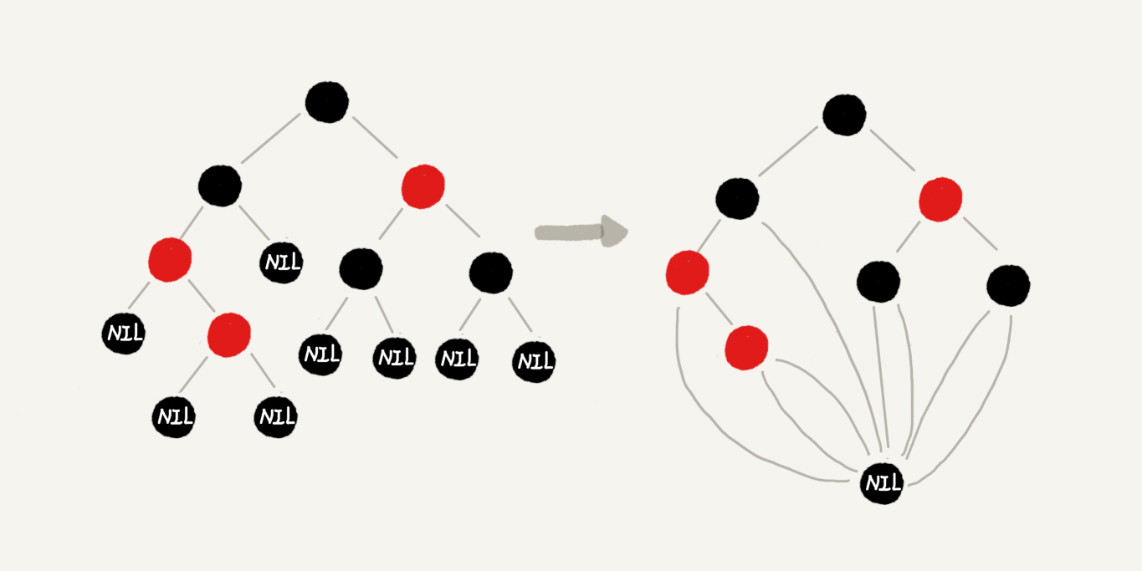
10.跳表
我们都知道二分查找算法,有它的局限性,具体可以参考文章。二分查找算法的局限性,主要体现在它需要连续存储结构,才能根据随机访问特性快速的实现二分,并且数组的内容必须是有序的。
那么,如果数据存储在链表中,就真的没法用二分查找算法了吗?
实际上,我们只需要对链表稍加改造,就可以支持类似“二分”的查找算法。我们把改造之后的数据结构叫作跳表(Skip list)。它确实是一种各方面性能都比较优秀的动态数据结构,可以支持快速的插入、删除、查找操作,写起来也不复杂,甚至可以替代红黑树(Red-black tree)。
10.1跳表的定义
对于一个单链表来讲,即便链表中存储的数据是有序的,如果我们要想在其中查找某个数据,也只能从头到尾遍历链表。这样查找效率就会很低,时间复杂度会很高,是 O(n)。
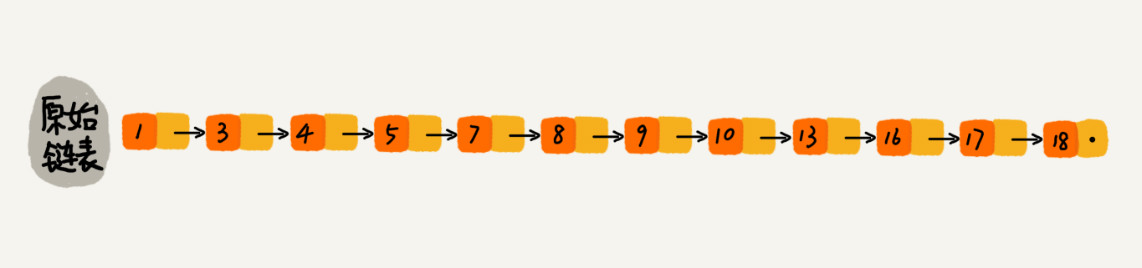
每两个结点提取一个结点到上一级,我们把抽出来的那一级叫作索引或索引层。
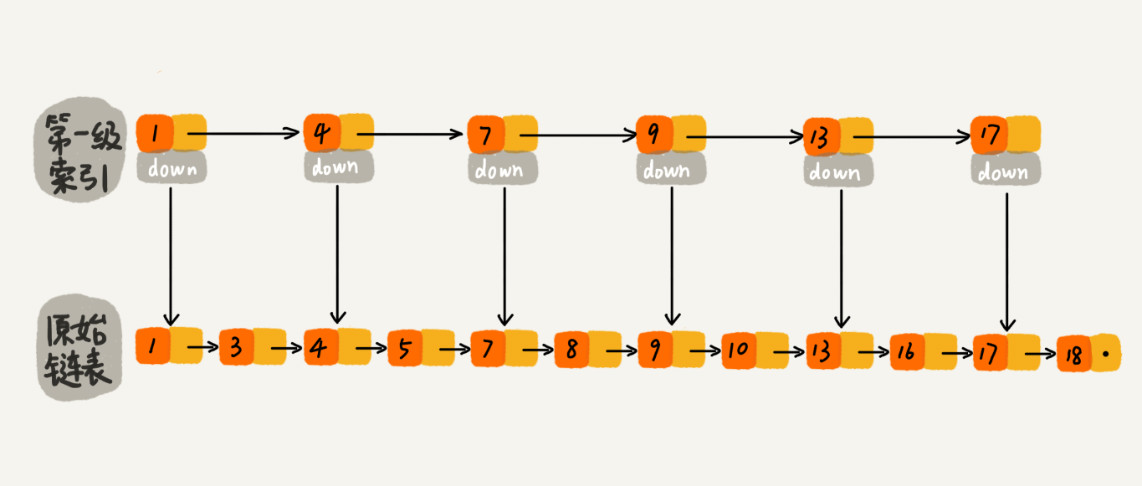
如果我们现在要查找某个结点,比如 16。我们可以先在索引层遍历,当遍历到索引层中值为 13 的结点时,我们发现下一个结点是 17,那要查找的结点 16 肯定就在这两个结点之间。然后我们通过索引层结点的 down 指针,下降到原始链表这一层,继续遍历。这个时候,我们只需要再遍历 2 个结点,就可以找到值等于 16 的这个结点了。这样,原来如果要查找 16,需要遍历 10 个结点,现在只需要遍历 7 个结点。
可以发现,加了一层索引之后,查找一个结点需要遍历的结点个数减少了,也就是说查找效率提高了,一般的,我们可以针对数据的规模来添加多层索引。前面讲的这种链表加多级索引的结构,就是跳表。
10.2复杂度分析
时间复杂度分析
如果链表里有 n 个结点,会有多少级索引呢?按照我们刚才讲的,每两个结点会抽出一个结点作为上一级索引的结点,那第一级索引的结点个数大约就是 n/2,第二级索引的结点个数大约就是 n/4,第三级索引的结点个数大约就是 n/8,依次类推,也就是说,第 k 级索引的结点个数是第 k-1 级索引的结点个数的 1/2,那第 k级索引结点的个数就是 n/(2^k)。假设索引有 h 级,最高级的索引有 2 个结点。通过上面的公式,我们可以得到 n/(2^h)=2,从而求得 h=log2n-1。如果包含原始链表这一层,整个跳表的高度就是 log2n。我们在跳表中查询某个数据的时候,如果每一层都要遍历 m 个结点,那在跳表中查询一个数据的时间复杂度就是 O(m*logn)。那这个 m 的值是多少呢?按照前面这种索引结构,我们每一级索引都最多只需要遍历 3 个结点,也就是说 m=3,为什么是 3 呢?我来解释一下。假设我们要查找的数据是 x,在第 k 级索引中,我们遍历到 y 结点之后,发现 x 大于 y,小于后面的结点 z,所以我们通过 y 的 down 指针,从第 k 级索引下降到第 k-1 级索引。在第 k-1 级索引中,y 和 z 之间只有 3 个结点(包含 y 和 z),所以,我们在 K-1 级索引中最多只需要遍历 3 个结点,依次类推,每一级索引都最多只需要遍历 3 个结点。
所以在跳表中查询任意数据的时间复杂度就是 O(logn)。这个查找的时间复杂度跟二分查找是一样的。换句话说,我们其实是基于单链表实现了二分查找,是不是很神奇!!!
但是它也不是十分完美,因为它的算法本质是通过空间来换时间,索引越多,空间复杂度越高。
空间复杂度分析
假设原始链表大小为 n,那第一级索引大约有 n/2 个结点,第二级索引大约有 n/4 个结点,以此类推,每上升一级就减少一半,直到剩下 2 个结点。如果我们把每层索引的结点数写出来,就是一个等比数列。
这几级索引的结点总和就是 n/2+n/4+n/8…+8+4+2=n-2。所以,跳表的空间复杂度是 O(n)。也就是说,如果将包含 n 个结点的单链表构造成跳表,我们需要额外再用接近 n 个结点的存储空间。
当然,这里的分析都是针对每两个结点抽一个结点到上级索引,这个间隔的结点个数并不是固定死的,如果把结点间隔扩大,那么空间复杂度也会相应的降低,但是时间复杂度肯定也会相应的提高。所以我们可以根据数据规模,使用场景需要来平衡时间和空间的效率,使得某一个特定场景拥有最大的时间空间效益。
11.散列表
Hash算法,大家应该都了解过,本章节不展开介绍hash算法的种类或者实现,只单纯讲一下散列算法。散列表就是一种算法思想,它的本质就是利用散列表,把O(n)级别的时间复杂度操作直接编程常数级别的,是不是一听就觉得很神奇。
来看一道之前刷pat遇到的题目吧,题目比较简单,就是用到的hash散列思想。
问题:给出N个正整数,再给出M个正整数,问这M个数中的每个数分别是否在N个数中出现过,其中N,M≤10^5,且所有正整数均不超过10^5.例如N=5, M=3,N个正整数为{8,3,7,6,2},欲查询的M个正整数为{7,4,2},于是后者中只有7和2在N个正整数中出现过,而4是没有出现过的。
对这个问题,最直观的思路是:对每个欲查询的正整数x,遍历所有N个数,看是否有一个数与x相等。这种做法的时间复杂度为O(NM),当N和M都很大(10^5级别)时,显然是无法承受的,没错我一开始就只想到了这一种解题思路,很简单暴力,但是也很无脑耗时。
那么,一般来讲耗时长的算法,都是可以通过提高空间复杂度来减小时间复杂度的,也就是很重要很重要的空间换时间的思想。
散列表就是这种思想的最好体现,以下就是该问题的C语言实现。
#include<cstdio>
const int maxn = 10010;
bool hashTable[maxn] = {false};
int main(){
int n,m,x;
scanf("%d%d",&n,&m);
for(int i =0;i<n;i++){
scanf("%d",&x);
hashTable[x] = true;
}
for(int i=0;i<m;i++){
scanf("%d",&x);
if(hashTable[x]==true){
printf("YES\n");
}else{
printf("NO\n");
}
}
return 0;
}Output
3 2
1 2 3
1
YES
2
YES更多的关于散列函数以及解决散列冲突的内容请参考文章
本文将持续更新,后期将持续整理并添加各数据结构和算法(仅限于本文中已经罗列出来的数据结构和算法,其它的内容,请查看我的algo专栏,我将持续更新并完善这个专栏,欢迎各位好心人能多提供帮助和资料)的使用场景和纵向对比,敬请关注。
本人还只是个小菜鸟,本博客收集了很多网上已有的内容,主要包括了极客时间《数据结构与算法之美》——王争(本人已付费购买该专栏,支持付费),以及中国大学MOOC陈越老师、何钦铭老师开设的《数据结构》课程(可以免费报名参加,墙裂推荐)还有算法笔记(胡凡、曾磊著)(主要是为了刷pat)的内容,如果文中有描述不当的地方请在留言区指出(十分感谢),如果某些内容引用出处我忘记贴上或者冒犯了你的权益,请告知一下,很抱歉,我将立马删除并重新整理。
如果有好的参考资料或者思考也欢迎大家提供,十分感激。
参考资料
- https://zh.wikipedia.org/wiki/%E6%A0%91_(%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84)
- 《算法笔记》第9章
- 中国大学MOOC——数据结构_陈越、何钦铭
- 《数据结构与算法之美》——极客时间专栏,王争
加载全部内容