Google 2019年10月23号发表在Nature（《自然》《科学》及《细胞》杂志都是国际顶级期刊，貌似在上面发文两篇，就可以评院士了）上，关于量子计算（基于 Sycamore芯片）的最新进展的论文，受到国内外同行及媒体的广泛关注，包括中科大量子科学家 — 潘建伟及其团队。IBM表示不服，Google不管。下面让我们逐字逐句来看他们的论文吧，对于争论的事务，自己下功夫下来搞清楚。

Quantum supremacy using a programmable superconducting processor

基于可编程的超导处理器实现的量子霸权 

 相关资源：https:/https://img.qb5200.com/download-x/doi.org/10.1038/s41586-019-1666-5

 接收日期：2019年7月20日

 核准日期：2019年9月20日

 在线发布：2019年10月23日

Abstract

引言

量子计算机吹牛逼说，对于特定的计算任务，基于量子处理器的计算机，其速度要比经典处理器成指数级增长。根本的挑战在于构建一个能够在海量的计算空间上运行量子算法的高保真处理器。我们的报告是关于，一个基于53量子比特实现的可编程的超导量子芯片，在2⁵³（约10¹⁶）的计算状态空间创建了一个量子态的故事。

我们用经典模拟验证了重复实验测量结果的采样概率分布。我们的Sycamore处理器采样一个量子电路100万次，大约花了200秒——我们的基准表明，同样的任务最先进的超级计算机大约需要花费10000年。相较于所有已知的经典算法，对于这个特定的计算任务，用实验实现的量子优越性在速度方面的显著提升，预示着一个期待已久的计算范式。

Main

正文

早在20世纪80年代，有鉴于经典计算机在模拟大型量子系统时成本高昂，理查德·费曼（Richard Feynman）就提出量子计算机将是解决物理、化学问题的有效工具。将费曼的设想付诸现，实构成了重大的实验和理论挑战。

首先，一个能够在足够巨大的计算空间（hibert）进行计算并且以低错误率提供量子加速的量子系统，工程上是否可行？其次，我们能否制定一个对于经典计算机很难但是对于量子计算机比较简单的问题？通过在我们的超超导量子处理器上运算这样的一个基准任务，我们解决了这2个问题。我们的实验实现了量子优越性，这是全面实现量子计算的征程的里程碑。

在实现里程碑的过程中，我们证明了量子加速在现实世界是可达到的，也没有被任何未知的物理定律所排出。量子优越性也预示着嘈杂的中型量子（NISQ，笔者：嘈杂意味着不稳定，噪音严重）技术时代的到来。我们论证的基准任务已经立即应用于生成可认证的随机数（S. Aaronson，手稿正则准备中）；这个新的计算能力的原始应用可能包括优化机器学习、材料科学和化学。然而，实现完全意义的量子计算（例如，Shor的分解算法）仍然有待于技术的飞越以制造容错逻辑的量子比特。

为了达成量子优越性，我们取得了一系列的技术进步，从而为纠错铺平了道路。我们研制了可以同时执行跨两个维度量子矩阵的快速高保真门。我们使用了强大的新工具：交叉熵基准，在组件和系统层面对处理器进行了校准和基准测试。最后，为了精确预测整个系统的性能，我们使用了组件级的保真度，从而进一步证明当扩展到大型系统时量子信息的行为符合预期。

A suitable computational task

合适的计算任务

为了证明量子优越性，我们在采样量子电路的伪随机输出任务中，比较我们的量子处理器和最新的经典计算机。随机电路是基准测试的一个合适选择，因为它门不具有结构，因此可以有限地保证计算硬度。我们设计的电路通过重复应用单量子和双量子逻辑运算实现了一组量子的纠缠。采样量子电路的输出生成了一串比特串，例如｛0000101, 1011100, …｝。由于量子干扰的存在，比特串的概率分布类似于在激光散射中的光干扰产生的强模型的斑点，因此有些比特串比其它的更容易出现。随着量子比特的数量（宽度）和们循环数量（深度）的增加，概率分布经典计算的难度成指数级增加。

我们使用称为交叉熵基准测试的方法来验证量子处理器是否正常工作，该方法将通过比较实验观察的每个比特串的频率与通过经典计算机的模拟计算得出的对应理想概率。对于给定的电路，我们收集测得的比特串{xi}并且计算线性交叉熵基准的保真度（另请参见补充信息），这是我们测得的比特串的模拟概率的平均值：

F_XEBY= 2ⁿ<P(x_i)>_i  ‐ 1

其中n是量子比特的总数，P(x_i) 是为理想的量子电路计算的位串 xi 的概率，并且平均值超过了观察到的比特串。直观地讲，F_XEB和我们采样高概率的比特串的频率相关。当量子电路没有错误的时候，其概率分布呈指数分布 （请参见补充信息），从这个分布采样将使得F_XEB = 1。另一方面，从均匀分布采样将得到：⟨P(xi)⟩i = 1/2ⁿ ,F_XEB  = 1。F_XEB的值介于0和1之间，表示电路运行时没有错误发生的概率。概率（P(x_i) ）必须从经典模拟量子电路得到，因此在至高无上的量子优越性上面计算F_XEB十分棘手。然而，通过某些简化的电路，我们可以估计出在宽和深量子电路上满载运行的处理器的定量保真度。

 我们的目标是通过足够宽和深的电路实现足够高的F_XEB，这样经典计算的成本将高的难以承受。这是一个艰巨的任务，因为我们的逻辑门并不完美，我们打算构造的量子态对错误也很敏感。在算法运行过程中，单个比特或则相位的翻转将彻底重构斑点图案并且导致保真度逼近0（请参见补充信息）。因此，为了宣称量子的优越性，我们需要一个能够以非常低的错误率运行程序的量子处理器。

Building a high-fidelity processor

构建高保真处理器

我们设计了一个名为“Sycamore”的量子处理器，它由54个特兰蒙量子比特的二维阵列组成，其中每个量子位可调耦合到一个矩形格子的四个最近的相邻接点。选择这个连接是为了与使用表层代码的纠错向前兼容。这个设备的一项关键系统进步是它实现了单量子比特和双量子比特运算的高保真度，不单单是孤立的，而且可以在许多量子比特上同时进行门运算和现实计算。我们接下来讨论重点，也请参见补充信息。

在一个超导量子比特里，传导电子会凝聚成宏观量子态，这样电流和电压会机械地呈现出量子态。我们的处理器使用特兰蒙量子比特，可以将其视为拥有5-7 G赫兹的主频的非线性超导谐振器。其量子比特被编码为谐振电路的两个最低量子本征态。每个特兰蒙都有两个控制器：一个微波驱动器来激发量子比特，以及一个磁通量控制器来调制频率。每个量子比特被连接到用于读出量子比特状态的线性谐振器。如图1所示，每个量子比特同时通过一个新的可调耦合器连接到其相邻的量子比特。我们的耦合器设计允许我们快速将量子比特—量子比特耦合从完全关停调整到40 M赫兹。1个量子比特无法正常运转，所以这个设备用了53个量子比特和86个耦合器。

 　　　　　　　　　　图.1 : Sycamore 处理器

为了金属化和约瑟夫森连接，处理器用铝制造，并使用铟制造两个硅晶片之间的凸点。芯片用引线粘合到超导电路板上，并在稀释冰箱中冷却至20 mK以下，以将环境热能降低到大大低于量子比特能。处理器通过滤波器和衰减器连接到处于室温的电子设备，该设备可合成控制信号。使用频率复用技术可以同时读取所有量子比特的状态。我们用两级低温放大器来增强信号，该信号被数字化（在1 G赫兹频率时为8比特）并在室温下通过数字化实现解复用。为了完全控制量子处理器，我们总共设计了277个数模转换器（在1G赫兹频率时为14比特）

 我们通过驱动25纳秒的微波脉冲来执行单量子比特门，该微波脉冲会以量子频率共振，同时关闭量子比特-量子比特耦合。脉冲经过整形，从而最大程度地避免了过渡到更高的特兰蒙状态。由于两级系统缺陷，门的性能会随频率产生很大的变化，杂散微波模式会与控制线和读出谐振器相耦合，量残余的杂散耦合于量子比特、磁通噪声和脉冲失真。有鉴于此，我们优化了单量子比特操作频率以减免这些错误机制。

我们使用上述交叉熵基准测试协议对单量子比特门的性能进行基准测试，降低到单量子比特级别（n = 1），以测量在单量子比特门期间发生错误的概率。在每个量子比特上，我们应用数量可变的m个随机选择的门，并在许多序列上测量F_XEB的平均值；随着m的增加，误差会累积、F_XEB的平均值会下降。我们用[1 − e₁ /（1 − 1 / D²）] ^m对该衰减建模，其中e₁是Pauli误差概率。在这种情况下，状态（希尔伯特）的空间量纲，D = 2ⁿ，等于2，它校正了误差与理想态部分重叠的去极化模型。该过程类似于更典型的随机基准测试，但支持非Clifford门的集合，并且可以将消退相干误差与相干控制误差区分开。然后，我们重复了所有量子比特同时执行单量子比特门的实验（图2），而错误率仅仅表现出微小的增长，表明我们设备的微波干扰率很低。

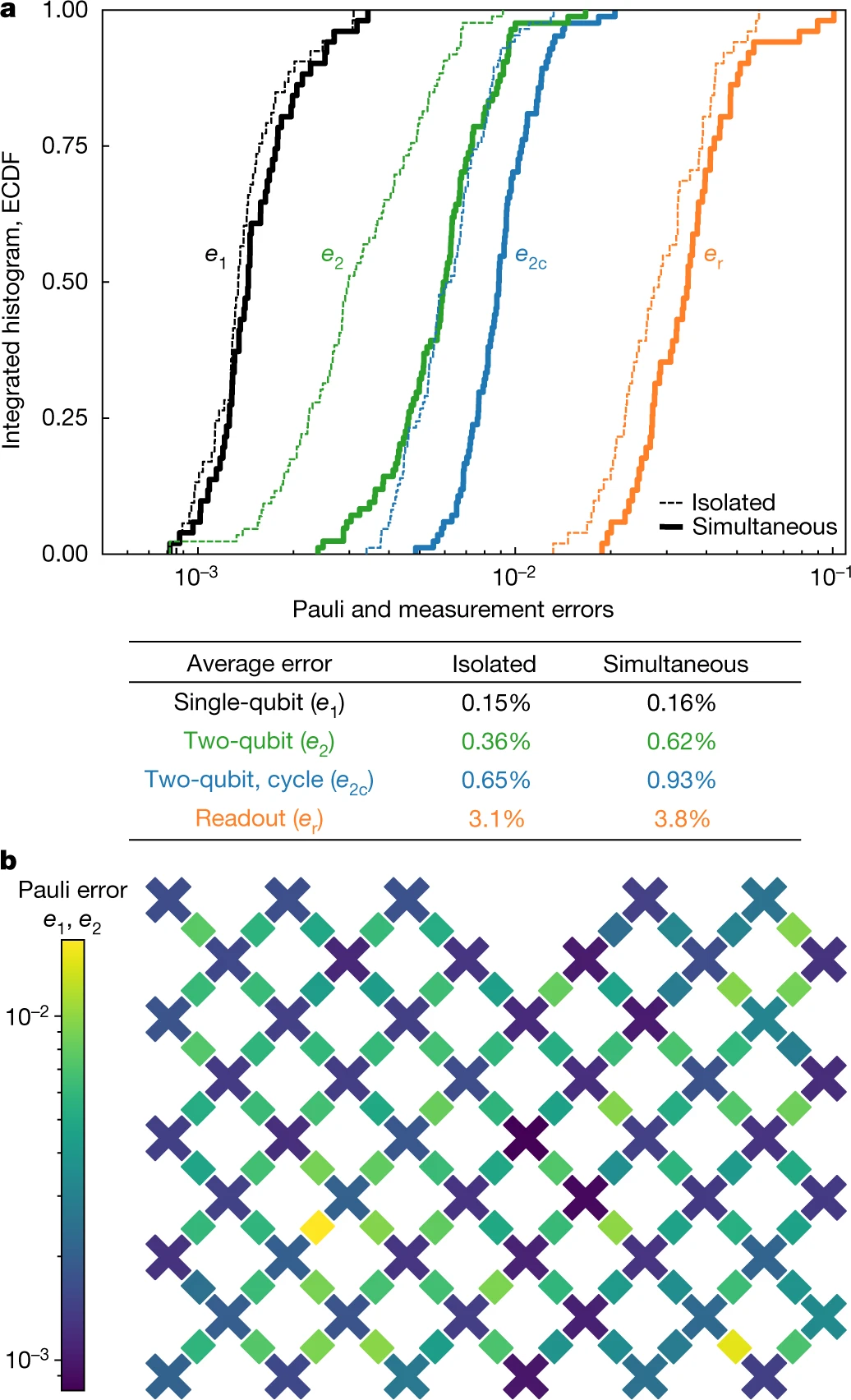
 　　　　　　　　图.2 : 全系统的 Pauli 和 测量错误

我们通过持续打开20 M赫兹耦合12 纳秒并使相邻的量子位共振来执行类似iSWAP的两个量子比特纠缠门，从而允许量子比特可以交换激励。在此期间，量子比特还经历了受控相位（CZ）的交互作用，该交互作用来自于更高级别的特兰蒙。优化每对量子比特的两个量子比特门限频率轨迹，是为了减少在优化单量子比特工作频率时所要考虑的相同错误机制。

To characterize and benchmark the two-qubit gates, we run two-qubit circuits with m cycles, where each cycle contains a randomly chosen single-qubit gate on each of the two qubits followed by a fixed two-qubit gate. We learn the parameters of the two-qubit unitary (such as the amount of iSWAP and CZ interaction) by using FXEBFXEB as a cost function. After this optimization, we extract the per-cycle error e2c from the decay of FXEBFXEB with m, and isolate the two-qubit error e2 by subtracting the two single-qubit errors e1. We find an average e2 of 0.36%. Additionally, we repeat the same procedure while simultaneously running two-qubit circuits for the entire array. After updating the unitary parameters to account for effects such as dispersive shifts and crosstalk, we find an average e2 of 0.62%.

对于整个实验，我们在同步操作期间用两个量子比特元测量每一对，而不是所有对的标准门，生成量子电路。典型的两个量子比特门是一个全iSWAP，并且拥有1/6的全CZ。绝不使用单独校准的门来限制演示的通用性。例如，1个量子比特门和任意给定对中的两个唯一的量子比特门可以组成可控NOT（CNOT）门。高保真“教科书似的门”，例如CZ或√iSWAP ，的制作正在紧锣密鼓地进行。

找到了单个门的错误率和读数后，我们可以将量子电路的保真度建模为所有门和测量的0错误操作概率的乘积。我们最大的随机量子电路有53个量子比特，1113个单量子比特门，430个双量子比特门，每个量子比特一个亮度，我们估计其总保真度为0.2%。由于F_XEB的不确定度为1 /N_s-√1/ N_s（其中Ns是样本数），因此这个保真度应该可以通过数百万次的测量来分辨。我们的模型推测，纠缠越来越大的系统不会引入超出我们在单比特和两比特级别上测量的误差之外的其他错误源。 在下一节中，我们将了解该假设的成立情况。

Fidelity estimation in the supremacy regime

优越性的逼真度估算

 我们的伪随机量子电路生成器的门序列如 图3 所示。此算法的一个周期由应用于所有量子的单量子（从｛√X, √Y, √Z｝随机选择），紧跟着的成对的量子比特上的两个量子比特门组成。组成“优越性电路”的门序列旨在最小化为创造一个高纠缠态的电路深度，而这正是计算复杂度和经典硬度所需。

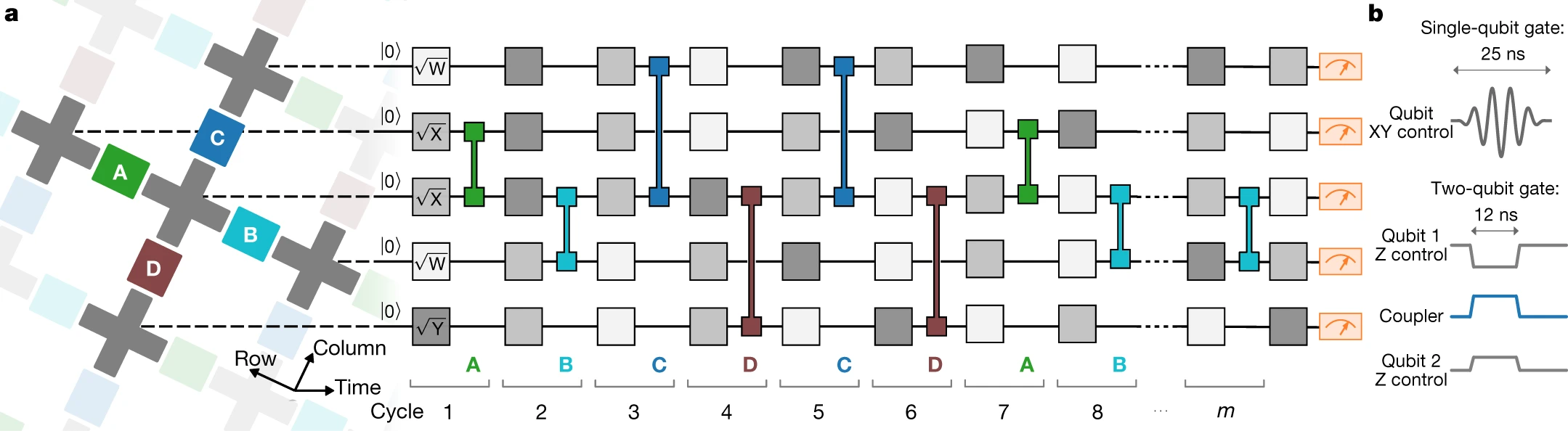
 　　　　　　　　　　　　　　　　　　图.3 : 量子优越性电路的控制操作

尽管我们无法在至高无上的体系中计算F_XEB，但是我们可以通过降低电路的复杂度的三个变体来评估它。在“贴片电路”中，我们移除掉了两个量子比特门的一部分（占两个量子比特门总数的一小部分），将电路分分割成两个空间上隔离的，没有相互作用的量子比特补丁。然后我们用可以轻松计算出保真度的补丁的乘积作为总的保真度。在“消除电路”中，我们沿切片仅去除了最初的两个量子比特门的一小部分，允许补丁之间的纠缠，这在维持了仿真可行性的同时更紧密地模拟了整个实验。最终，我们也可以运行同我们的优越性电路有着相同的门数的全“验证电路”，但却与在传统上容易模拟的多的两电子门序列有着不同的模式（也请参见补充信息）。比较这些三个变体让我们能够在接近优越性制度的过程中追踪系统保真度。

我们首先检查补丁版本和删节版本的验证电路是否能与多达53量子比特的完整验证电路产生相同的保真度，如图4所示。每个数据点，我们通常在10个电路实例中采集 N_s = 5 × 10⁶的总样本，每个实例的区别仅在于在每个周期中单个量子门的选择不同。我们也显示F_{XEB的预测值，}该值是通过将单量子和双量子比特门的0错误率和测量值相乘而得到的（也请参见补充信息）_。尽管在计算复杂度和纠缠存在巨大差异，这个预测值、补丁及消除的保真度都对应的全电路的保真度吻合的很好。这让我们对消隐电路可以用于准确估计更为复杂电路的保真度充满信心。

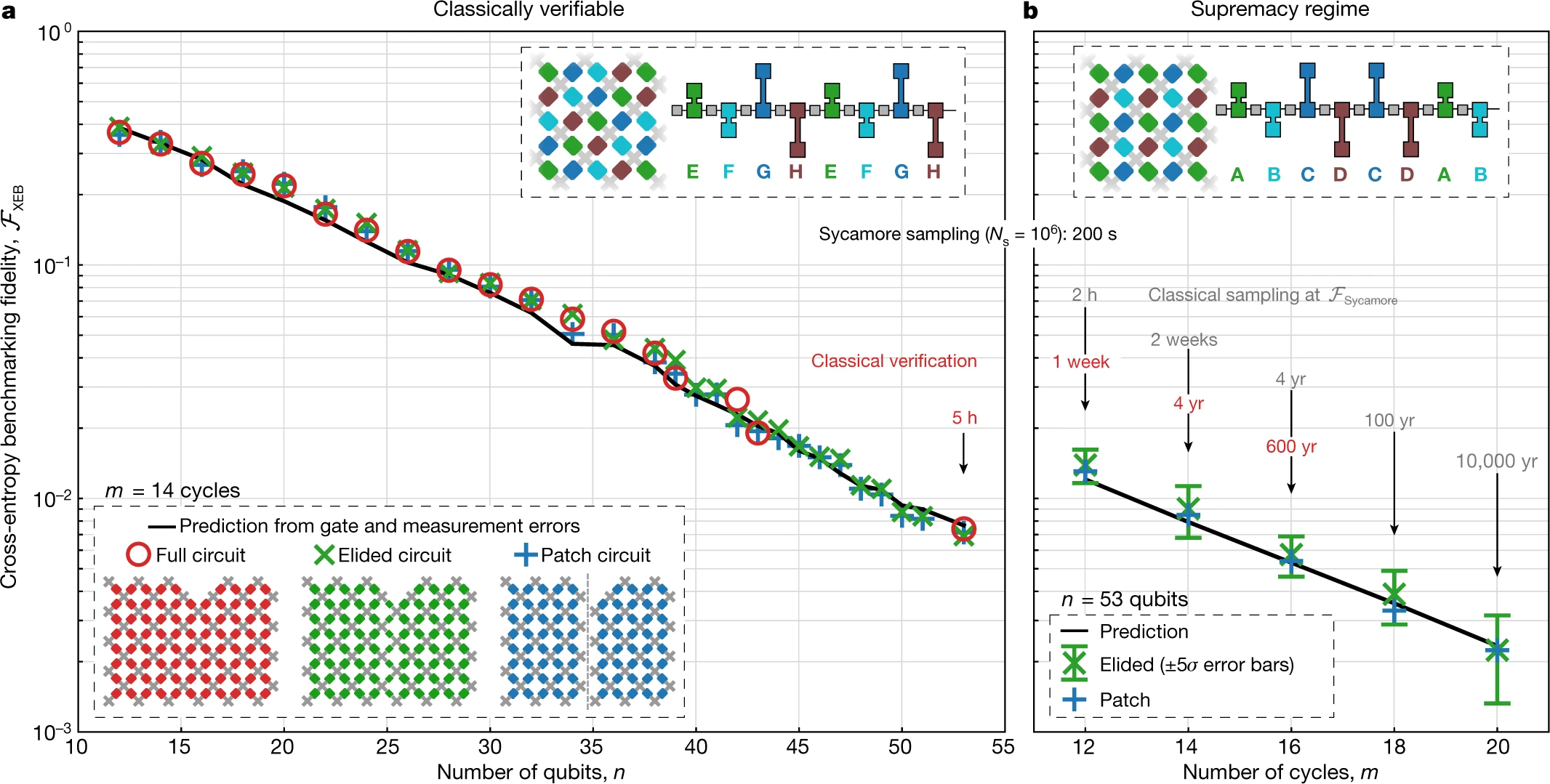
　　　　　　　　　　　　　　　　图.4 : 量子优越性的证明

保真度仍可以直接被验证的最大电路有53个量子比特和一个简化处理过的门电路。100万个内核以0.8%的保真度对这些随机电路进行采样需要花费130秒，相较于单核，量子处理器有百万倍的加速。

我们现在继续对计算最复杂电路进行基准测试，这个只是2个比特门的重排列。在图4中，我们显示了通过不断增加深度，针对53量子比特的全优越性电路的补丁版和消隐版本测得的F_XEB。对于有53个量子比特和20个周期的最大电路，我们在10个电路实例上搜集了 N_s = 30 × 10⁶

样本，对于消隐电路得到的F_XEB = (2.24±0.21)×10⁻³。基于5σ的置信度，我们断定在量子处理器上运行这些电路的平均保真度至少大于0.1％。我们预期 图4b的全部数据应具有近似的保真度，但是由于仿真时间（红色数字）需要很长时间才能检查，我们将数据归档（参见“数据可用性”部分）。这部分数据因此处于量子至上的状态。

The classical computational cost

经典计算的成本

我们在经典计算机的实验中模拟量子电路有2个墓地：（1））通过使用可能简化的电路计算F_XEB来验证我们的量子处理器和基准测试方法（图4a），(2)估算F_XEB以及对最困难的电路进行采样的经典成本（图4b）。多达43个量子比特，我们使用Schrödinger算法，该算法模拟了完整量子态的演化；Jülich超级计算机（100,000核、250 TB）运行了最大的样例。超过此大小，则没有足够的随机存取存储器（RAM）来存储量子的状态。对于更多的量子，我们使用运行在Google数据中心的混合Schrödinger-Feynman算法来计算单个比特串的幅度。在使用类似费曼路径积分的方法连接它们之前，该算法将电路拆分为两个量子比特补丁，并使用Schrödinger方法有效地模拟每个补丁。尽管具有更高的内存效率，但随着路径深度与连接补丁的门的数量呈指数增长，随着电路深度的增加，Schrödinger-Feynman算法的计算量也呈指数增长。

为了估算优越性电路的经典计算成本(图4中的灰色数字），我们在Summit超级计算机以及Google集群上都运行了部分量子电路的仿真，从而推断出其全部成本。在此推断中，我们通过扩展F_XEB的验证成本来认定采样的计算成本，例如，一个0.1%减少了约1000的花费。在当今世界上功能最强大的Summit超级计算机上，我们使用了一个受费曼路径积分启发的方法，该方法在低深度下效率最高。当m = 20时，张量无法合理地放入节点内存中，因此我们只能在m=14时测量运行时间，因此我们估计以1％的保真度采样300万个比特串将需要一年。

在谷歌云服务器上，我们预估使用Schrödinger-Feynman算法以0.1％的保真度在m = 20时运行相同的任务将耗费50万亿个核/小时，并消耗1皮瓦时的能量。从这个角度考虑，从角度来看，对量子处理器上的电路采样三百万次需要600秒，而采样时间受控制硬件的通信的限制；实际上，量子处理器的实际上，净量子处理器的净时间仅为30秒左右。所有电路的比特串样本都已在线存档（请参见“数据可用性”部分），以激励开发和测试更高级的验证算法。

有人可能会怀疑算法创新可以在多大程度上增强经典模拟效果。我们的假设基于复杂理论的认知，即算法任务的成本是电路大小的指数。的确，在过去的几年中，模拟算法已经得到了稳步的提升。我们预计最终将实现比报告里提到的更低的仿真成本，但是我们也期望更大型的量子处理器在硬件方面的改进将持续超越它们。

Verifying digital error model

验证数字错误模型

基于量子错误校正理论的一个关键假设是——量子态错误可考虑数字化和本地化。基于这样的一个数字模型，演化量子态中的所有错误都可能通过散布在电路中的一组局部保利误差（位翻转或相位翻转）来表征。由于持续振幅是量子力学的基础，所以需要测试量子系统中的错误是否可以被视为离散的和概率的。确实，我们实验的观察结果证明该模型对我们处理器是有效的。我们系统的保真度可以通过一个简单的模型很好地预测，在该模型中，每个门的各自的特征保真度相乘起来（图4）。

为了能成功被数字化误差模型描述，系统的相关误差得很小才行。我们通过选择随机化和解相关误差的电路，优化控制以最大程度地减少系统误差和泄漏以及设计比相关噪声源（如1 / f磁通噪声）运行得更快的门，从而在我们的实验中达成了这一点。通过在高达2⁵³号希尔伯特空间对预测性不相关的误差模型的演示，可以表明我们可以构建一个系统，在该系统中量子资源（例如纠缠）不会过于脆弱。

The future

未来

基于超导量子比特的量子处理器现在可以处理，量纲为2⁵³ ≈ 9 ×10¹⁵的希尔伯特（Hilbert）空间的计算，超出了当今最快的经典超级计算机的上限。据我们所知，此次试验标记了只能在量子处理器运行的第一个计算。量子处理器因此达成了量子优越性的制度。我们希望他们的计算能力将继续以双倍指数的比率增长：模拟量子电路的经典成本随着计算量的增加而呈指数级的增长，而硬件的提升将可能遵循量子处理器当量的摩尔定律，即每隔几年计算量此计算量就翻倍。为了支撑双指数级的增长率并最终提供运算著名的，如Shor 或者Grover ，量子算法所需的计算量，量子误差修正的工程学将成为关注的焦点。

Bernstein 和 Vazirani 阐述的扩展自Church–Turing的论文，断言任何合理的模型都可以由图灵机器有效的模拟。

Data availability

数据可用性

用于本次研究形成和分析的数据库可在我么公开的树妖（Dryad）仓库上获得 (https:/https://img.qb5200.com/download-x/doi.org/10.5061https://img.qb5200.com/download-x/dryad.k6t1rj8)。

在线内容

 任何方法、额外参考、自然研究的报告摘要、源数据、扩展数据、补充信息、确认书、同行评审信息；作者贡献和利益冲突的详细信息； 以及数据和代码可用性均可在 https:/https://img.qb5200.com/download-x/doi.org/10.1038/s41586-019-1666-5 得到。

初次尝试翻译，错误之处必不在少，欢迎批评指正。翻译真是不容易，我前前后后花了超过10个小时

附：

1）英文论文下载： Quantum supremacy using a programmable superconducting processor 

2）「量子霸权」真的来了：谷歌论文正式在《自然》杂志发表；借助 54 个量子比特的 Sycamore 芯片实现（附论文）

*****************************************************************************************************

精力有限，想法太多，专注做好一件事就行

• 我只是一个程序猿。5年内把代码写好，技术博客字字推敲，坚持零拷贝和原创
• 写博客的意义在于锻炼逻辑条理性，加深对知识的系统性理解，锻炼文笔，如果恰好又对别人有点帮助，那真是一件令人开心的事

*****************************************************************************************************