基于曝光融合框架的对比度增强算法

论文题目《A New Image Contrast Enhancement Algorithm Using Exposure Fusion Framework》翻译以及分析

摘要

低光图像不利于人眼观察和计算机视觉算法识别，因为它们的可见度较低。虽然已经提出了许多图像增强技术来解决这个问题。但是现有方法不可避免地存在对比度过低和过高的情况。在本文中，我们提出了一种精确的对比度增强的算法。具体来说，我们首先使用光照估计技术为图像融合设计权重矩阵。然后，我们用相机的响应模型合成多重曝光图像。接下来，我们找到最佳的曝光率，为了合成图像在原始图像曝光不足的区域进行更好的曝光。最后，输入图像和合成图像根据权重矩阵进行融合以获得图像增强的结果。实验表明，相比其他优秀的方法，我们的方法可以得到对比度和亮度失真更少的结果。

1. 研究现状

图像增强技术广泛用于图像处理中。一般来说，它可以使输入图像看起来更好，并且更适合于特定算法进行处理。对比度增强，作为一种增强技术，可以在图像中显示曝光不足区域的信息。目前有大量的对比度增强的技术，主要包括基于直方图，基于Retinex和基于除雾的方法的增强技术。

彩色图像可以用三维数组表示。最简单的对比度增强的方法是对每个对象执行相同的处理过程。例如，最早的图像增强方法使用非线性单调函数进行灰度级映射。

考虑到不同灰度级别中元素的不均匀分布，因此直方图均衡化（HE）被广泛用于改善对比度。许多直方图均衡化的扩展方法将亮度保存和对比度限制考虑进去。但是基于直方图均衡化的方法总是会过度增强和产生不切实际的结果。在模仿在人类视觉系统中，Retinex理论也广泛用于图像增强。通过将反射图与光照图分开，基于Retinex的算法可以明显增强细节。但是这些方法在高对比度区域容易产生伪像。近年来，一些方法应用除雾技术来增强对比度并获得良好的主观视觉效果。但是这些方法也可能会因为对比度过度增强而导致颜色失真。

尽管图像对比度增强方法研究了几十年，但是好的增强效果仍然没有很好的定义。此外，现有的弱光增强算法也没有提供参考如何定位过度增强和不足增强区域。我们注意到不同的图像曝光度可以作为增强算法的参考，如图1所示。随着曝光度的增加，一些低曝光区域变得曝光良好。增强的结果应保持曝光良好的区域保持不变，而曝光不足的区域则增强。与此同时，增强区域的对比度应与正确曝光区域保持一致。

在本文中，我们提出了一个新的框架来帮助缓解欠/过度增强的问题。我们的框架基于相机响应模型从输入图像合成的多张曝光图像的曝光融合。基于我们的框架，我们提出了一种增强算法与其他几种相比最先进的方法，可以获得更少的对比度和亮度失真的结果。

2. 本文方法

2.1 曝光融合框架

在许多室外场景中，相机无法使所有像素曝光良好，因为它的动态范围是有限的。如图1所示尽管我们可以通过增加曝光量显示一些曝光不足的区域，与此同时曝光良好的区域可能同时曝光过度。为了让所有像素的图像曝光良好，我们可以融合这些图像：
\[ R^c = \sum\limits_{i=1}^{N}W_i*P_i^c \]
其中 \(N\) 是图像数量，\(P_i\) 是曝光集合中的第 \(i\) 个图像，\(W_i\) 是第 \(i\) 个图像的权重图，\(c\) 是三个颜色通道的索引，\(R\) 是增强后的结果。三个颜色分量是相等的，所有像素是不均匀的：曝光良好的像素具有较大的权重，曝光不良的像素权重较小。权重已标准化，因此 \(\sum_{i=1}^{N}W_i=1\)。

问题是具有其他曝光设置的图像不适用于图像增强问题。幸运的是，使用不同的曝光度拍摄的照片是高度相关的。在我们的早期工作中，我们提出了相机响应模型以准确描述这些图像之间的关联，以便我们从输入图像生成一系列图像。两张不同曝光度的图像的映射函数，我们称为亮度转换函数（BTF）。给定曝光率 \(k_i\) 和 亮度转换函数 \(g\)，我们可以映射输入图像 \(P\) 到曝光集合中的第 \(i\) 个图像：
\[ P_i=g(P, k_i) \]
在本文中，我们仅以一定的曝光融合输入图像本身来降低复杂度，如图2所示。融合图像定义为：
\[ R^c=W*P^c+(1-W)*g(P^c,k) \]

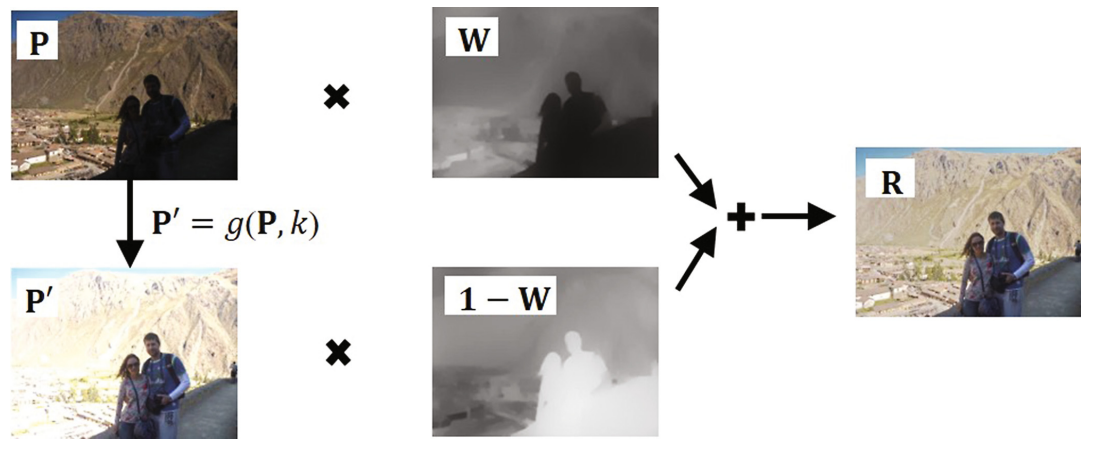
增强问题可分为三个部分：\(W, g, k\) 的三个参数的估计。在以下小节中，我们将一一解决这三个问题。

2.2 权重矩阵估计

\(W\) 是增强算法的关键，其目的是增强曝光不足区域的低对比度，而保留曝光良好区域的对比度。我们需要给曝光良好的像素分配较大的权重值，给曝光不足的像素分配较小的权重值。直观地来说，权重矩阵与场景光照正相关。由于高度光照区域有更大的可能性获得更好的曝光，应分配给大的权重值以保持它们的对比度。我们计算权重矩阵为：
\[ W=T^{\mu} \]
其中 \(T\) 是场景光照图，\(\mu\) 是控制增强程度的参数。场景光照估计位置映射 \(T\) 通过优化的方法解决。

（1）优化问题

亮度分量可以作为场景光照的估计。我们采用亮度分量作为光照估计的初始值：
\[ L(x)=max _{c\in \{R,G,B\}}P_c(x) \]
对于每个单独的像素x。理想照明在结构相似的区域具有局部一致性。换句话说，\(T\) 应该保持有意义的图像的结构并去除纹理边缘。在文献[5]中，我们可以通过最优方程得到 \(T\) ：
\[ \min _{\mathbf{T}}\|\mathbf{T}-\mathbf{L}\|_{2}^{2}+\lambda\|\mathbf{M} \circ \nabla \mathbf{T}\|_{1} \]
其中 \(\|*\|_2\) 和 \(\|*\|_1\) 分别是 \(\ell_2\) 和 \(\ell_1\) 范数。一阶微分滤波器 \(\nabla\) 包含水平方向梯度 \(\nabla_h\mathbf{T}\) 和垂直方向梯度 \(\nabla_v\mathbf{T}\)。\(M\) 是权重矩阵，\(\lambda\) 是系数。方程式的第一项最小化初始图 \(\mathbf{L}\)和场景光照图\(\mathbf{T}\)，而第二项为保证 \(\mathbf{T}\) 的平滑性。

\(\mathbf{M}\) 的设计对于光照图的细化很重要。局部窗口中的主要边缘比具有复杂图案的纹理贡献了更多的相似方向梯度。因此，包含有意义的边缘窗口中的权重应小于仅包含一个窗口的边缘纹理。因此，我们将权重矩阵设计为
\[ \mathbf{M}_{d}(x)=\frac{1}{\left|\sum_{y \in \omega(x)} \nabla_{d} \mathbf{L}(y)\right|+\epsilon}, \quad d \in\{h, v\} \]
其中\(| ∗ |\) 是绝对值运算符，\(\omega（x）\) 是以像素 \(x\) 和 \(\epsilon\) 是一个很小的常数，以避免分母为零。

（2）封闭解

为了简化复杂度，我们将Eq.6近似为在文献[5]中公式：
\[ \min _{\mathbf{T}} \sum_{x}\left((\mathbf{T}(x)-\mathbf{L}(x))^{2}+\lambda \sum_{d \in\{h, v\}} \frac{\mathbf{M}_{d}(x)\left(\nabla_{d} \mathbf{T}(x)\right)^{2}}{\left|\nabla_{d} \mathbf{L}(x)\right|+\epsilon}\right) \]
可以看出，该式子现在仅涉及二次项。 令\(md\)，\(l\)，\(t\) 和 \(\nabla_dl\) 分别表示向量化的\(\mathbf{M}_d\)，\(\mathbf{L}\)，\(\mathbf{T}\) 和 \(\nabla_d \mathbf{L}\)。 然后可以通过求解以下线性函数直接获得解
\[ \left(\mathbf{I}+\lambda \sum_{d \in\{h, v\}}\left(\mathbf{D}_{\mathbf{d}}^{\top} \operatorname{Diag}\left(\mathbf{m}_{d} \oslash\left(\left|\nabla_{d} \mathbf{l}\right|+\epsilon\right)\right) \mathbf{D}_{\mathbf{d}}\right) \mathbf{t}=1\right. \]
其中\(\varnothing\)是按元素划分，\(\mathbf{I}\) 是单位矩阵，运算符 \(Diag(v)\) 是用向量 \(v\) 构造对角矩阵，\(\mathbf{D}_d\) 是Toeplitz矩阵来自具有前向差异的离散梯度算子。我们的光照图估计方法和文献[5]的主要区别是设计矩阵\(\mathbf{M}\) 的权重。我们采用了简化的策略，可以产生在文献[5]中相似的结果。基于Retinex的其他光照分解技术方法可以运用到这里来找到权重矩阵 \(\mathbf{W}\)。

2.3 相机响应模型

在我们的早期工作中，我们提出了一个称为Beta-Gamma的相机响应模型校正模型在文献[[16]中。我们模型的BTF定义为：
\[ g(\mathbf{P},k)=\beta\mathbf{P^{\gamma}}=e^{b(1-k^a)\mathbf{P^{(k^a)}}} \]
其中 \(\beta\) 和 \(\gamma\) 是该模型的两个参数，可以通过相机参数 \(a\) ，\(b\) 和曝光率 \(k\) 计算得到。我们假设没有任何相机信息，并使用固定相机参数（\(a = -0.3293\) ，\(b = 1.1258\)）可以适配大多数相机。

2.4 确定曝光率

在本小节中，我们找到最佳的曝光率，以便合成图像在原始图像曝光不足的区域中曝光良好。第一，我们排除曝光良好的像素，并获得整体上低曝光图像。我们只需提取低光照像素为：
\[ \mathbf{Q}=\{\mathbf{P}(x)\mathbf{T}(x)<0.5\} \]
其中 \(\mathbf{Q}\) 仅包含曝光不足的像素。不同曝光下图像的亮度变化很大但是颜色基本相同。因此，我们在估计 \(k\) 只考虑了亮度分量。亮度分量 \(\mathbf{B}\) 定义为三个通道的几何平均值：
\[ \mathbf{B}:=\sqrt[3]{\mathbf{Q}_r\circ\mathbf{Q}_g\circ\mathbf{Q}_b} \]
其中\(\mathbf{Q}_r\)，\(\mathbf{Q}_g\) 和 \(\mathbf{Q}_b\) 分别是输入图像 \(\mathbf{Q}\) 的红色，绿色和蓝色通道。 我们使用几何平均值代替其他定义（例如算术平均值和加权算术平均值），因为它具有相同的BTF所有三个颜色通道的模型参数（ \(\beta\) 和 \(\gamma\)），如下所示：
\[ \begin{aligned} \mathbf{B}^{\prime} &:=\sqrt[3]{\mathbf{Q}_{r}^{\prime} \circ \mathbf{Q}_{g}^{\prime} \circ \mathbf{Q}_{b}^{\prime}} \\ &=\sqrt[3]{\left(\beta \mathbf{Q}_{r}^{\gamma}\right) \circ\left(\beta \mathbf{Q}_{g}^{\gamma}\right) \circ\left(\beta \mathbf{Q}_{b}^{\gamma}\right)}=\beta(\sqrt[3]{\mathbf{Q}_{r} \circ \mathbf{Q}_{g} \circ \mathbf{Q}_{b}})^{\gamma} \\ &=\beta \mathbf{B}^{\gamma} \end{aligned} \]
曝光良好的图像的可见度高于曝光不足的图像，它可以为人类提供更丰富的信息。因此，最优的 \(k\) 应该提供最多的信息。为了衡量信息的数量，我们使用图像熵来定义：
\[ \mathcal{H}(\mathbf{B})=-\sum_{i=1}^{N} p_{i} \cdot \log _{2} p_{i} \]
其中 \(p_i\) 是B的直方图的第i个bin，用于计算数据数量在 \([\frac{i}{N},\frac{i=1}{N}]\)，N是bin数（ \(N\) 通常设置为256）。最后，通过最大化图像增强的亮度熵来计算最佳 \(k\) 值：
\[ \hat{k}=\underset{k}{\operatorname{argmax}} \mathcal{H}(g(\mathbf{B}, k)) \]
最优的 \(k\) 值可以通过一维最小化求解。为了改善计算效率，我们在优化 \(k\) 时将输入图像的大小调整为 \(50 \times 50\)。

3. 实验对比

为了评估我们方法的性能，我们在公开数据集与几种最新技术（AMSR [9]，LIME [5]，Dong [4]和NPE [14]）进行比较。这五个公共数据集分别为：VV，LIME-data [5]，NPE [14]（NPEdata，NPE-ex1，NPE-ex2和NPE-ex3），MEF [10]和IUS [8]。 MEF和IUS是多重曝光数据集，我们从每个多重曝光中选择一个弱光图像进行评估。

3.1 实验细节

在我们的算法中，\(\mu\) 是控制整体增强程度的参数。当\(\mu = 0\)时，所得 \(\mathbf{R}\) 等于 \(\mathbf{P}\)，即没有增强效果。 当时，曝光不足像素和曝光良好像素均被增强。 当 \(\mu> 1\) 时，像素可能会饱和，从而导致 \(R\) 遭受细节损失。 为了更好的增强，同时保留曝光良好的区域，我们将 \(\mu\) 设置为1/2。

为了保持比较的公平性，我们增强算法的参数在所有实验中都是固定的：\(\lambda = 1\)，\(\epsilon=0.001\) ，\(\mu= 1/2\)，和局部窗口\(\omega(x)\)的大小为5。我们算法中最耗时的部分是光照图的优化。 我们采用多分辨率共轭梯度 \((\mathbf{O}(N))\) 来有效地求解它。 为了进一步加快我们的算法，我们通过对输入图像进行下采样方法解决 \(\mathbf{T}\)，然后将生成的 \(\mathbf{T}\) 向上采样到原始大小。 如果我们向下采样一次，增强结果中没有视觉差异，但是计算效率大大提高了。

3.2 对比度失真

如前所述，仅曝光度不同的图像可用作参考来评估增强结果准确性。 DRIM（动态范围独立指标）[1]可以测量图像对比度的失真，而无需考虑图像亮度变化。 我们用它来可视化对比增强结果与参考图像之间的差异。

如图3所示，该方法得到失真最小的结果。 Dong的结果出现严重的对比度失真。 尽管AMSR可以恢复细节，但对比度明显下降使结果看起来暗淡和虚幻。 相比之下，LIME的结果看起来像有点生动，但它们会导致放大不可见的对比度。 图5显示更多示例在视觉上进行比较。

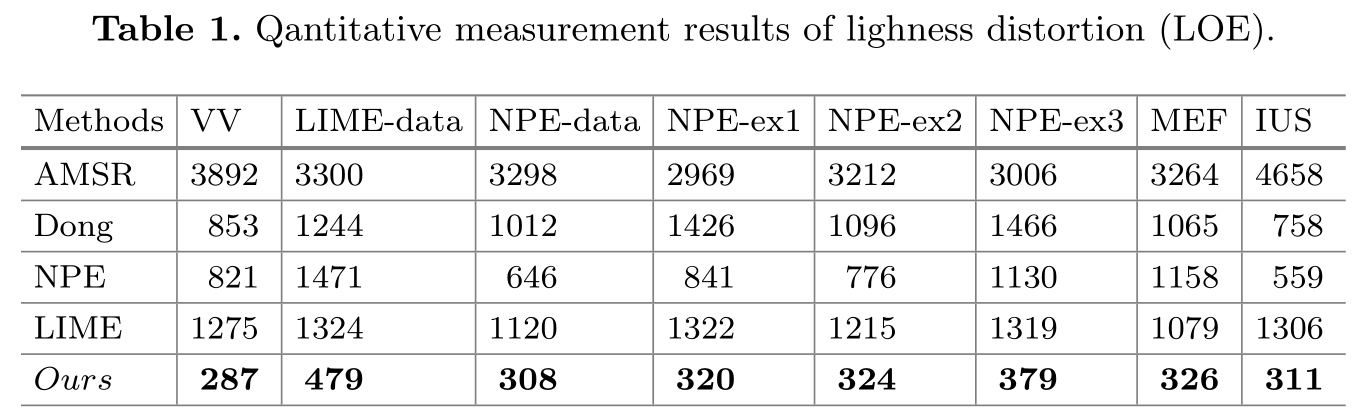
3.3 亮度失真

我们用我们使用亮度等级误差（LOE）客观地衡量增强结果的亮度失真。 LOE定义为：
\[ LOE=\frac{1}{m}\sum_{x=1}^{m}RD(x) \]
对于像素 \(x\), 其中 \(RD(x)\) 是原始图像 \(P\) 和增强后\(P^{'}\) 之间的相对亮度阶差，其定义如下：
\[ RD(x)=\sum_{y=1}^{m} U(\mathbf{L}(x), \mathbf{L}(y)) \oplus U\left(\mathbf{L}^{\prime}(x), \mathbf{L}^{\prime}(y)\right) \]
其中 \(m\) 是像素数量，\(\oplus\) 表示异或运算符，\(\mathbf{L}(x)\)，\(\mathbf{L}^{\prime}(x)\) 分别是输入图像和增强后位置 \(x\) 处的亮度分量。 如果 \(p>= q\)，函数 \(U(p，q)\) 返回1，其他情况为0。

正如[5,14]中所建议的那样，下采样用于计算LOE降低复杂度。 由于RD将随着像素数量m的增加而增加，我们注意到LOE随着图片下采样为不同尺寸而变化。 因此，我们将所有图像下采样到固定大小。 具体来说，我们均匀收集100行和列，以形成 \(100\times100\) 的下采样图像。如表1所示，我们的算法在所有数据集中均优于其他算法。 这个意味着我们的算法可以很好地保持图像的自然性。 我们也提供了图4中两种情况的亮度失真的可视化，从中我们可以发现我们的结果具有最小的亮度失真。AMSR的结果失去了全局的亮度等级，并具有最大的亮度失真。尽管LIME的结果在视觉上令人愉悦，但它们也存在亮度不足的失真。 Dong和NPE的结果只能在曝光良好的区域保留亮度顺序。

4. 结论

在本文中，我们提出了曝光融合框架和增强算法提供精确的对比度增强的算法。 基于我们的框架，我们解决了三个问题：（1）我们借鉴了光照估算技术获得图像融合的权重矩阵。（2）通过相机响应模型来合成多重曝光图像。（3）我们找到了最好的曝光率，使合成图像在原始图像曝光不足的区域曝光良好。 最终的增强结果是通过融合根据权重矩阵对输入图像和合成图像进行处理。实验结果表明我们方法相比现阶段最先进的方案的有效性。
可以在我们的项目网站上找到更多测试结果：https://baidut.github.io/OpenCE/caip2017.html。

5. 主要参考文献

1. Aydin, T.O., Mantiuk, R., Myszkowski, K., Seidel, H.P.: Dynamic range independent image quality assessment. ACM Trans. Graph. (TOG) 27(3), 69 (2008)
2. Beghdadi, A., Le Negrate, A.: Contrast enhancement technique based on local detection of edges. Comput. Vis. Graph. Image Process. 46(2), 162–174 (1989)
3. Chen, S.D., Ramli, A.R.: Minimum mean brightness error bi-histogram equalization in contrast enhancement. IEEE Trans. Consum. Electron. 49(4), 1310–1319(2003)
4. Dong, X., Wang, G., Pang, Y., Li, W., Wen, J., Meng, W., Lu, Y.: Fast efficient algorithm for enhancement of low lighting video. In: 2011 IEEE International Conference on Multimedia and Expo, pp. 1–6. IEEE (2011)
5. Guo, X.: Lime: a method for low-light image enhancement. In: Proceedings of the 2016 ACM on Multimedia Conference, pp. 87–91. ACM (2016)
6. Ibrahim, H., Kong, N.S.P.: Brightness preserving dynamic histogram equalization for image contrast enhancement. IEEE Trans. Consum. Electron. 53(4), 1752–1758 (2007)
7. Jobson, D.J., Rahman, Z., Woodell, G.A.: A multiscale retinex for bridging the gap between color images and the human observation of scenes. IEEE Trans. Image Process. 6(7), 965–976 (1997)
8. Karaduzovic-Hadziabdic, K., Telalovic, J.H., Mantiuk, R.: Subjective and objective evaluation of multi-exposure high dynamic range image deghosting methods (2016)
9. Lee, C.H., Shih, J.L., Lien, C.C., Han, C.C.: Adaptive multiscale retinex for image contrast enhancement. In: 2013 International Conference on Signal-Image Technology & Internet-Based Systems (SITIS), pp. 43–50. IEEE (2013)
10. Ma, K., Zeng, K., Wang, Z.: Perceptual quality assessment for multi-exposure image fusion. IEEE Trans. Image Process. 24(11), 3345–3356 (2015)
11. Peli, E.: Contrast in complex images. JOSA A 7(10), 2032–2040 (1990)
12. Reza, A.M.: Realization of the contrast limited adaptive histogram equalization (clahe) for real-time image enhancement. J. VLSI Signal Process. Syst. Signal Image Video Technol. 38(1), 35–44 (2004)
13. Wang, C., Ye, Z.: Brightness preserving histogram equalization with maximum entropy: a variational perspective. IEEE Trans. Consum. Electron. 51(4), 1326– 1334 (2005)
14. Wang, S., Zheng, J., Hu, H.M., Li, B.: Naturalness preserved enhancement algorithm for non-uniform illumination images. IEEE Trans. Image Process. 22(9), 3538–3548 (2013)
15. Xu, L., Yan, Q., Xia, Y., Jia, J.: Structure extraction from texture via relative total variation. ACM Trans. Graph. (TOG) 31(6), 139 (2012)
16. Ying, Z., Li, G., Ren, Y., Wang, R., Wang, W.: A new low-light image enhancement algorithm using camera response model, manuscript submitted for publication (2017)