python实现三壶谜题的示例详解
仙九玖玖 人气:0前言
有一个充满水的8品脱的水壶和两个空水壶(容积分别是5品脱和3品脱)。通过将水壶完全倒满水和将水壶的水完全倒空这两种方式,在其中的一个水壶中得到4品脱的水。
一、算法思想
算法分析
- 采用的算法思想是将某个时刻水壶中水的数量看作一个状态,用一个长度为3的数组表示。
- 初始状态便为[8,0,0],再拓展他的下一结点的可能结构。
- 若下一结点的结构已经被拓展过了便放弃,若没有拓展过则加入拓展列表(open_list)中。然后递归上述操作。
- 直到拓展列表(open_list)为空或者找到目标为止。
思想图解
这里的第一个数就代表着是那个8品脱的瓶子,依次分别是8品脱,5品脱,3品脱
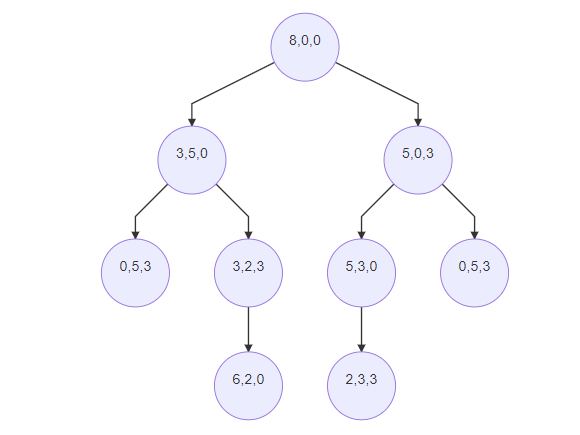
就如同上图一样,使用层次遍历一次一次递归扩展新的结点,知道找到4品脱的水或者无结点可扩展为止(类似于广度优先遍历)。
二、代码展示
1.创建树节点结构
节点包括两个属性,一个属性是数组类型的,存储当前三个水壶的容量状态,另一个属性是记录它是由哪个结点扩展过来的,以便找到解决路径:
class node: # 创建树节点 def __init__(self, data): self.data = data # 存储三个壶的容量状态 self.per = None # 存储上一时刻三个壶的容量状态
2.实现倾倒动作
由于这里只有三个壶,互相倾倒的方案可以枚举出来,所有我就没使用二重嵌套循环,而是使用一层循环:
def pour(n): # 扩展子节点
r_list = n.data # 记录当前三个水壶的容量状态
max_list = [8, 5, 3] # 水壶的最大容量
for i, j in ((0, 1), (0, 2), (1, 2), (1, 0), (2, 0), (2, 1)):
if r_list[i] != 0:
n_list = r_list.copy() # 初始化下一结点的水壶状态
if r_list[i] + r_list[j] > max_list[j]:
n_list[i] = r_list[i] - (max_list[j] - r_list[j])
n_list[j] = max_list[j]
else:
n_list[j] = r_list[i] + r_list[j]
n_list[i] = 0
flag = True # 记录水壶的状态是否已经发生过(扩展过)
for one in closed_list:
if one.data == n_list: # 比较当前水壶状态和以往记录过得水壶状态
flag = False
if flag:
print("扩展的新节点是:",n_list)
new_node = node(n_list) # 创建新节点存储水壶的新状态
new_node.per = n
open_list.append(new_node)
主递归函数
查看当前是否已经扩展到4品脱的水或者是否还有结点可以扩展。
def BFS_node(root_1): # 递归查找子节点的扩展状态以及查验是否找到4品脱的水壶
n = root_1
print("当前节点:",n.data)
if open_list is None:
return "没有找到4品脱的水"
nodelist = n.data
if 4 in nodelist:
print("找到了4品脱的水")
print_node(n)
return "找到了4品脱的水"
closed_list.append(open_list.pop(0))
pour(n)
print("*******")
BFS_node(open_list[0])
数据初始化
数据初始化,以及找到4品脱水后打印路径的打印函数。
def print_node(n): # 打印正确的水壶操作路径 if n.per == None: return "" print(n.data) print_node(n.per) # 初始化数据 root = node([8, 0, 0]) open_list = [root] # 存储已找到却未被扩展的子节点 closed_list = [] # 存储已找到且被扩展的子节点 BFS_node(open_list[0])
总结
主要是用广度优先遍历的思想和树结构,当然如果不在意找到4品脱的水的路径,其实没必要使用树结构。另外打印函数是从最后一层依次往上回溯的,所以显示的是倒序的路径。如果需要变成正向的话,可以加一个栈来实现。
加载全部内容