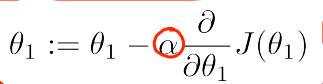梯度下降算法

梯度下降的目的：

在监督学习的线性回归问题中，我们要在大量的数据中去拟合一条曲线，得到一个预测函数，来预测下一次的值。
那么怎么得到这个预测函数呢？我们通过不断改变假设函数中的每个参数，直到代价函数的值最小的时候，假设函数中的参数就足够“完美”了，这个时候的假设函数也就能比较准确的预测下一次的值，也就称它为预测函数。

那么我们按照怎么一种规则来改变假设函数中的参数呢？梯度下降算法就是用来改变假设函数的参数的一种算法。

如果我们有一个两个参数θ1 θ2的假设函数。代价函数图如下：我们随机选取θ1 θ2的值，得到代价函数的值，我们的目标是到达图像的最低点，代价函数值最小。于是我们开始改变θ1 θ2的值，走下坡路。直到到达局部最低点。这个不断更新参数θ1 θ2的过程，就像在下山，梯度下降是不是很形象啊？

我们从最简单的例子说起：
假设函数：

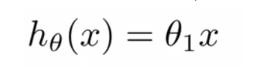
代价函数：

更改θ1的公式：

• 这里α是改变的‘步长’,它有边的式子是代价函数对参数θ1求偏导数，这个函数中也就是求导，在θ1上的斜率。当θ1在我们目标θ1的左边的时候，斜率是负数，减去一个负数也就是加一个正数。这个时候θ1变大，越来越接近我们的目标θ1值。如果θ1大于我们的目标θ1值的时候，斜率是正数，减去正数，θ1变小了，也是越来越接近我们的目标θ1。
• 但是我们要合理控制α的大小，如果α太小，梯度下降的步子就很慢。如果α太大，如第二幅图所示，θ1快到达目标θ1值的时候斜率是负数，这时候α太大，θ1减去一个很大的负数，就变成了加上一个很大的正数，超过了目标θ1的值。再进行一次更新θ1，θ1会减去一个更大的正数（斜率变大了），不断的远离目标θ1值。这个就欲哭无泪了。
  

在线性回归模型中，梯度下降算法如下

在梯度下降算法公式中：α代表学习速率，是代价函数对要改变的参数求偏导。

也就是每次梯度下降（更新参数），就进行一次这样的计算
下降一步，同时修改更新所有参数。

注意！
修改每次梯度下降是同时更新所有参数。方式是左图而不是右图：

批量梯度下降

Batch Gradient Descent
Batch Each step of gradient descent uses all the training examples.
批量梯度下降的每一步都使用了所有的训练实例。
也就是每次更新一次所有的假设函数中的参数值，就使用了全部的样本数据来求代价函数的值。
如果有超大量样本数据，你的α又比较小，那效率将会……别人家里全部的电器都会说话了，你还在这里梯度下降.
所以我们还有另外一种方式

随机梯度下降

随机梯度下降是每次修改一次所有的参数，只用一个样本数据。少了算法公式中误差平方累加的过程。
区别是：批量梯度下降收敛得慢，但是收敛的比较接近目标参数值。
随机梯度下降收敛的快，可能还没有用完整套数据，就已经收敛的差不多了，但是下降震荡的幅度大，收敛不够那么接近目标参数值。
此外还有小批量梯度下降，请自行脑补。。。