编译原理之语法分析-自下而上分析(四)

　　　　（一）LR(k)项目

　　　　　　LR(k)项目与之前SLR(1)中的项目有所不同，LR(k)项目是一个二元组[ 产生式，终结符 ]的形式

　　　　　　定义：使得每个项目都附带有k个终结符，项目是二元组，一般形式是[ A->α· β ，a1 a2 ....ak]，这样的项目称为LR(k)项目。k越大，LR(k)项目越多。

• • • 显然，从定义中我们能得出A->α· β是一个LR(0)项目，因为它后边二元组的终结符个数为0。
    • a1 a2 ..... ak是终结符，称为向前搜索符串（展望串）
    • α处于栈顶位置
    • 圆点后边的输入可以匹配 β a1 a2 ..... ak

　　　　（二）LR(1)项目

　　　　　　定义：我们只对k<=1的情形感兴趣，通过向前搜索一个符号就可以确定移进或归约，如果K=1，即LR(1)项目，[ A->α· β ，a ]。

• • • 对于任何移进或待约项目[ A->α· β ，a]（β ！=  ε），搜索符串a没有任何作用。
    • 向前搜索符a仅对归约项目[ A->α β · ，a]有意义。
      • 当它所属的状态呈现在栈顶且后续的输入符号为a时，才可以把栈顶上的αβ归约为A。
      • 当归约A->αβ(第i个产生式)时,a时前看符号。把ri填入到ACITON[ s，a ]中。　

　　　　　　LR(1)项目的构造：

• • • 对于项目[ A->α ·Bβ，a ]，添加[  B->γ ，b ] 到项目集，b属于First(βa)。
    • 与LR(0)相比，仅有闭包的计算方法不同。
    • 为构造有效的LR(1)项目集族我们需要两个函数CLOSURE和GO。　

　　　　　　　CLOSEURE(I)的定义：

　　　　　　　

 

　　　　　　　　GO的定义：

　　　　　　　　

　　　　(三)构造LR(1)文法分析表

　　　　　　下图中有一增广文法，求出它的项目集。

　　　　　　

 

　　　　　　 老规矩，直接上答案图，然后按步骤讲解。

 

 　　　　

 

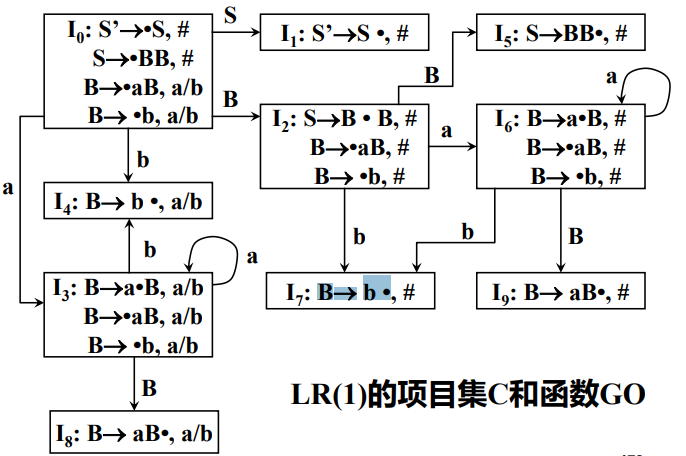
1. 1. 从S' -> ·S且项目集编号为0开始，S'为开始符号，二元组终结符部分是#，所以二元组为[ S' -> ·S，# ]。

• • • 根据定义,圆点后为S（非终结符），将S -> ·BB加入0号项目集，因为S->·BB中的S是从S'->S而来的，在二元组 [S'->·S，# ]求出Follow(S) = { # }，所以得出二元组[ S->·BB，# ]
    • 根据定义,圆点后为B（非终结符），将B -> ·aB加入0号项目集，求出S -> ·BB圆点后第一个符号(第一个B)的Follow集，或求出圆点后从第二个符号开始的(第二个B开始)的First集。求出First（B，#）={a,b},（注意First（B）中的B是S -> ·BB中的第二个B），所以得出二元组[ B -> ·aB,a | b ]。
    • 将B->B -> ·b加入0号项目集，(注意这里产生式左部的B，也是来自于S->·BB中的第一个B)，因此我们只需要求出Follow(第一个B)或者First(第二个B，#)即可，得出First(B)={a,b}，加入二元组[  B->·b, a | b ]
    • 至此0号项目集已经完成　　　　　　　　　　　　　　　　

 

　　　　　2.项目集0输入符号B进入项目集2，从S->B·B开始，这里的S来自于项目集0中的[S->·BB，#]，而S->·BB来自于[ S'->·S，# ]，因此项目集2中加入二元组[ S->B·B ，#]。

• • • 根据定义，S->B·B中，圆点后为非终结符，加入B -> ·aB，而产生式左部的B来自于项目集2中[ S->B·B ，# ]中的第二个B，所以求出Follow(第二个B)={ # }，或First(#)={ # }，所以加入二元组[ B -> ·aB ，#]。
    • 项目集2加入B->·aB之后还需要加入B->·b，这个B同样来自于项目集2中[ S->B·B ，# ]中的第二个B，所以求出Follow(第二个B)={ # }，或First(#)={ # }，所以加入二元组[ B->·b ，#]。
    • 至此2号项目集已经完成

　　　　　3.　项目集0输入符号a进入项目集3，从B->a·B开始，产生式左部的B来自于项目集0中的[ B->·aB，a | b]，而B->·aB又来自于S->·BB，所以求出Follow(第一个B)={ a,b }或First(第二个B，#)={ a,b }，所以项目集3中加入[ B->a·B ，a | b]

• • • 根据定义，B->a·B中圆点后为非终结符，加入B->·aB，继续找出产生式左部B的来源，来自于项目集3中[ B->a·B，a | b ]求出Follow（B）={a , b}，First（a|b）={a，b}，因此项目集3中加入二元组[B->·aB，a | b]。
    • 同样项目集3加入B->·b，继续找出产生式左部B的来源，来自于项目集3中[ B->a·B，a | b ]求出Follow（B）={a , b}，First（a|b）={a，b}，因此项目集3中加入二元组[B->·b，a | b]。
    • 至此3号项目集已经完成

　　　　因为项目集过多，这里只选出具有代表性的三个项目集解释，其他项目集可按该思路得出。　

　　　　总结：有一产生式 S -> xxx（x代表任意终结符或非终结符），就去查找该S的来源，然后找到源二元组[ E->x·SA，abc ]之后，求出Follow(S)，或　First（Aabc）即可。　　　

 　　　　　　下图是该文法的LR(1)分析表

　　　　　　　

 

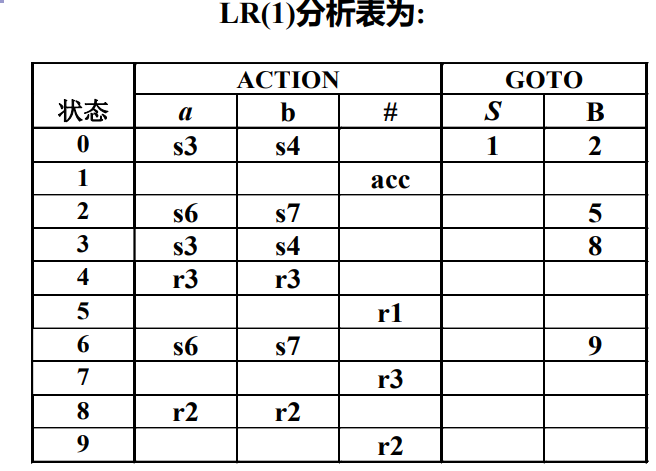
　　　　　　可以发现归约项目集为4、5、7、8、9，而再查看对应的的LR(1)项目集可以看出来：

• • • 4号项目集终结符为a，b，因此在ab所在列填入r3（Ri中的 i 为文法编号，第一个图）。
    • 5号项目集终结符只有#，因此只在#所在列填写r1。
    • 7号项目集终结符只有#，因此只在#所在列填写r3。
    • 8号项目集终结符为a，b，因此在ab所在列填入r2。
    • 9号项目集终结符只有#，因此只在#所在列填写r2。

　　　　　　表中其余内容与LR(0)和SLR(1)基本一致，这里就不再介绍。至此LR(1)分析表就构造完成。

　　　　　　

　　　　　   对于该文法再给出LR(0)和SLR(1)分析表，可以做一下对比理解，自己推下3个分析表如何构造：

　　　　　　　　

 

　　　　　　　　

 

 

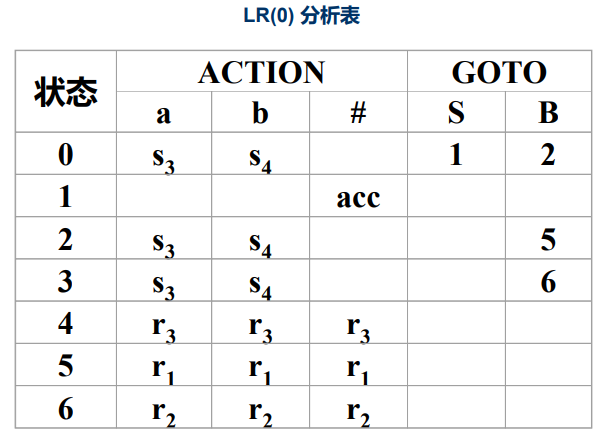
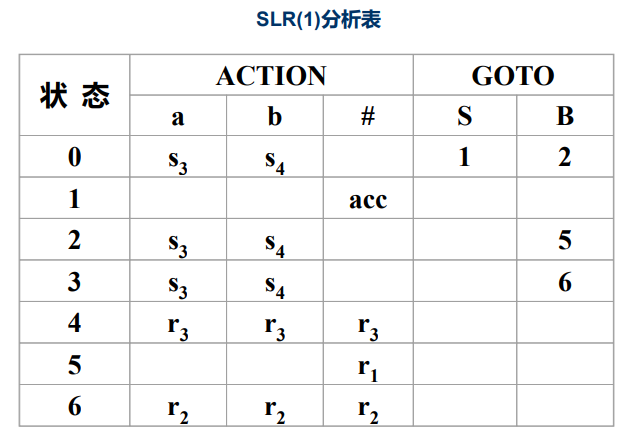
 　　　　　　　　最后给出三个分析表算法的系统语言：

　　　　　　　　

 

 

 

 　　　　　　　　　

 

 

 　　　　　　　　　　

 

 

 　　　　　　　　　　到此为止，就已经完成LR(0)、SLR(1)、LR(1)分析表的构造以及流程。

　　　　　　　　　　总结一下三个表流程(重点、重点、重点!!!)：

1. 1. 1. 1. 构造增广文法。
         2. 根据增广文法列出项目集
         3. 构造NFA（该步骤可以省略）
         4. 构造LR(0)DFA(这一步非常重要，如果DFA构造错误则分析表会出错，LR(0)和SLR(1)的DFA一样，LR(1)的DFA中产生式后需要计算终结符 )
         5. 判断是不是LR(0)文法，如果存在冲突则下一步，如果不存在冲突则该文法是LR(0)文法。(是LR(0)文法则一定是SLR(1）和LR(1)文法)
         6. 判断冲突能否用SLR(1)的解决方法消除，如果能消除则是SLR(1)文法，如果不是则下一步
         7. 根据LR(0)的DFA或SLR(1)的DFA(一元组形式)计算每个产生式的展望串，从而得出LR(1)的DFA（二元组形式）。
         8. 根据冲突项目集中终结符去判断能否消除冲突，如果S-R或R-R冲突的两个二元组中的终结符没有交集则视为可以消除冲突，如果不能消除至此则该文法不属于上述3个文法的任意一个。

 

 

　　　　　　　　　　　LALR文法就不再介绍了，如果有兴趣可以查看一下其他优秀的博客，至此自下而上分析法就已经介绍完毕(该博客为个人学习总结，如果错误或异议欢迎指出，谢谢。)