基于Python实现拉格朗日插值法

时间:2022-12-12 泡泡怡人气:0

一、拉格朗日的基本思想

拉格朗日插值法是以法国十八世纪数学家约瑟夫·拉格朗日命名的一种多项式插值方法。

许多实际问题中都用函数来表示某种内在联系或规律，而不少函数都只能通过实验和观测来了解。在若干个不同的地方得到相应的观测值,拉格朗日插值法可以找到一个简单函数,其恰好在各个现测的点取到观测到的值,这个函数可以是代数多项式,三角多项式等。

二、线性插值

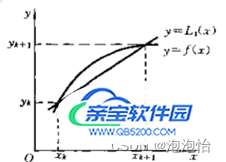
三、多个点

四、代码实现

def lagrange(xx,y):
    l=len(y)
    l_n = 0
    for k in range(l):
        xxx=xx.copy()
        x_k = xxx[k]
        xxx.pop(k)
        l_k = 1
        for i in range(len(xxx)):
            l_k *= (x - xxx[i]) / (x_k -xxx[i])
        l_n += y[k] * l_k
    return expand(l_n)

五、完整代码

import matplotlib.pyplot as plt
import numpy as np 
import pandas as pd
from sympy import expand
from sympy.abc import x
xx=[]
for i in range(7):
    xx.append(data['x'][i])
y=[]
for j in range(7):
    y.append(data['y'][j])
def lagrange(xx,y):
    l=len(y)
    l_n = 0
    for k in range(l):
        xxx=xx.copy()
        x_k = xxx[k]
        xxx.pop(k)
        l_k = 1
        for i in range(len(xxx)):
            l_k *= (x - xxx[i]) / (x_k -xxx[i])
        l_n += y[k] * l_k
    return expand(l_n)  
lagrange_interpolation_polynomial = lagrange(xx, y)
print("拉格朗日插值多项式为:",lagrange_interpolation_polynomial)
x2=np.linspace(-1,4,100)
y1=[]
for i in range(len(x2)):
    y1.append(lagrange_interpolation_polynomial.subs(x,x2[i]))
print(y1)
#绘制散点图,逼近函数
plt.figure(figsize=(8,4))
plt.scatter(xx,y,c='red')
plt.plot(x2,y1,'-')
plt.show()

六、pop（）函数

七、结果展示

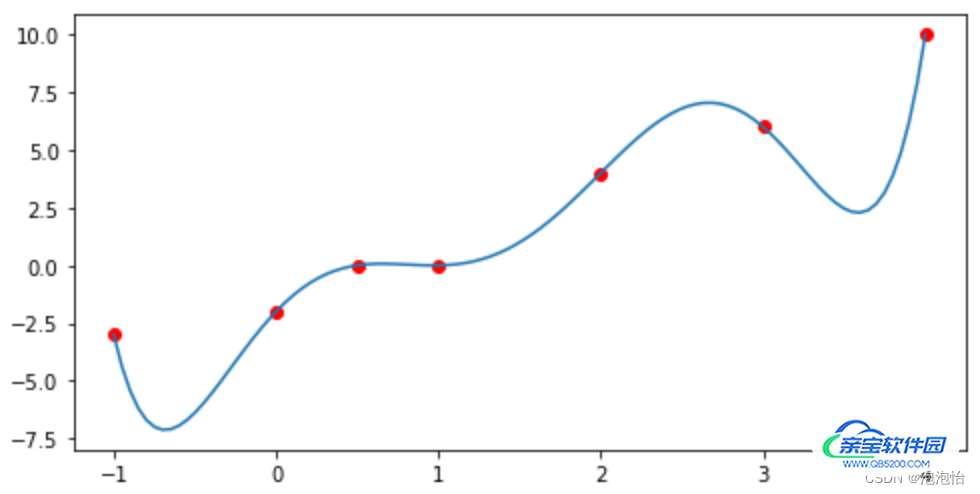
加载全部内容