Python中层次聚类的详细讲解
川川菜鸟 人气:0前言
层次聚类是流行的无监督学习算法之一。层次聚类所做的就是找到数据集中具有相似属性的元素,并将它们组合在一个集群中。最后,我们得到一个单一的大集群,其主要元素是数据点的集群或其他集群的集群。
一、聚类流程与基本原理
系统聚类法(hierarchical clustering method),又叫分层聚类法,是目前最常用的聚类分析方法。其基本步骤如下:假设样本中有n个样品,那么就先将这n个样品看作n类,也就是一个样品一个类,然后将性质最接近的两类合并为一个新的类,这样就得到n-1个类,接着从中再找出最接近的两个类,让其进行合并,这样就变为n-2个类,让此过程持续进行下去,最后所有的样品都归为一类,把上述过程绘制成一张图,这个图就称为聚类图,从图中再决定分为多少类。如下所示:
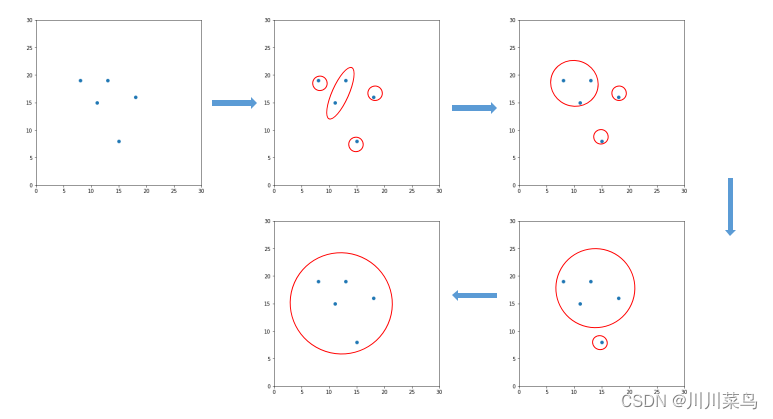
样点之间的相似度是根据距离来实现的,比如最短距离法、最长距离法、重心法、类平均法以及ward法。
最短距离法 :从两个类中找出距离最短的两个样品点。如下:
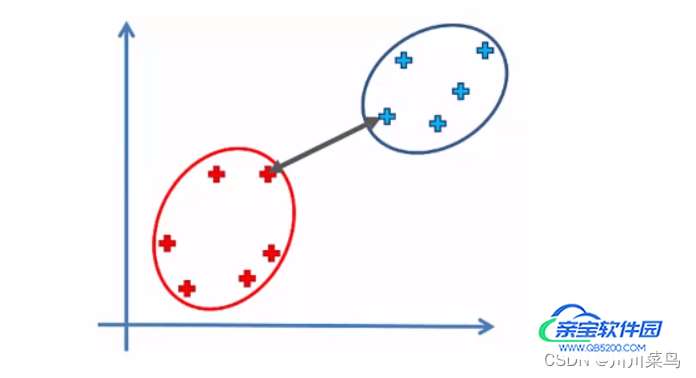
最长距离法 :同理如下:
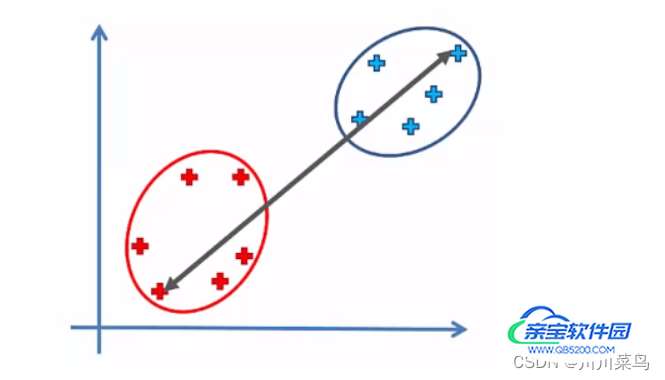
类平均法: 就是取两个类之间所有点的距离的平均值
重心法 :名如其法,如下
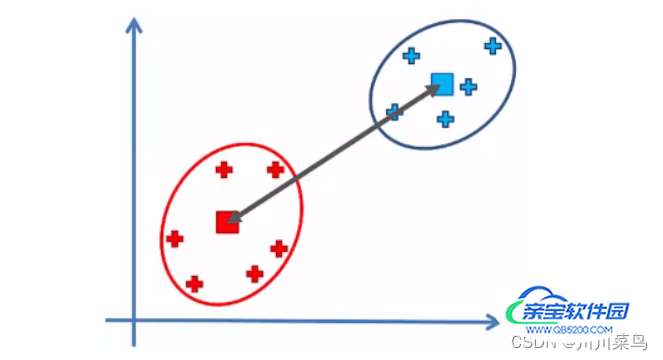
离差平方和法 :离差平方和法又叫Ward法,此方法查找聚合偏差。例如,如果我们有两个集群,我们可以假装将它们合并为一个集群,然后估计结果集群的质心。之后,我们找到新质心的所有点的平方偏差之和。对于不同的合并,我们将获得其他变化。因此,我们选择合并最小的距离作为我们的距离。
二、实现层次聚类
数据下载:点击这里下载
如下:
2.1 导入相关库
import numpy as np import matplotlib.pyplot as plt import pandas as pd
2.2 读取数据
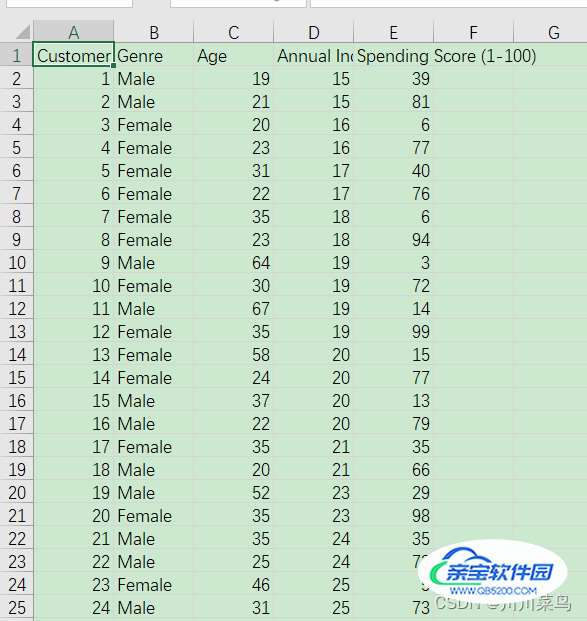
ourData = pd.read_csv('Mall_Customers.csv')
ourData.head()
如下:
我们将使用该数据集在Annual Income (k$)和Spending Score (1-100)列上实现我们的层次聚类模型。所以我们需要从我们的数据集中提取这两个特征:
newData = ourData.iloc[:, [3, 4]].values newData
如下:

可以看到数据不一致,我们必须对数据进行缩放,以使各种特征具有可比性;否则,我们最终会得到一个劣质的模型。原因是层次聚类,就像机器学习中的许多其他算法一样,是基于距离的(欧几里得距离)。
2.3 确定最佳集群数
在尝试对我们的数据进行聚类之前,我们需要知道我们的数据可以最佳地聚类到多少个集群。所以让我们首先在我们的数据集上实现一个树状图来实现这个目标:
import scipy.cluster.hierarchy as sch # 导入层次聚类算法
dendrogram = sch.dendrogram(sch.linkage(newData , method = 'ward')) # 使用树状图找到最佳聚类数
plt.title('Dendrogram') # 标题
plt.xlabel('Customers') # 横标签
plt.ylabel('Euclidean distances') # 纵标签
plt.show()
树状图,如下所示:
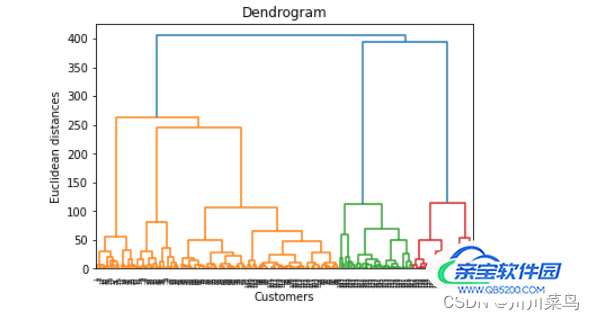
看上面的树状图,可以确定最佳聚类数;假设地,推断整个树状图中的所有水平线,然后找到不与这些假设线相交的最长垂直线。
越过那条最长的线,建立一个分界线。我们可以对数据进行最佳聚类的聚类数等于已建立的阈值所跨越的欧几里德距离(垂直线)的计数。
在我们刚刚获得的树状图中,没有延伸的水平线交叉的最长垂直线位于绿色部分。第三条线位于欧几里得距离 (110 - 250) 之间。将我们的阈值设为 150,获得的最佳聚类数为 5。知道我们的数据应该聚集到的最佳数量;我们现在可以训练我们的聚类模型来实现这个目标。
2.4 层次聚类模型训练
from sklearn.cluster import AgglomerativeClustering # n_clusters为集群数,affinity指定用于计算距离的度量,linkage参数中的ward为离差平方和法 Agg_hc = AgglomerativeClustering(n_clusters = 5, affinity = 'euclidean', linkage = 'ward') y_hc = Agg_hc.fit_predict(newData) # 训练数据
上面的代码训练了我们的模型,我们现在可以继续并可视化数据是如何聚集的:
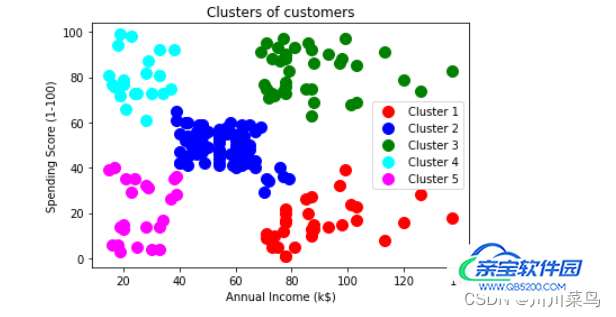
plt.scatter(newData[y_hc == 0, 0], newData[y_hc == 0, 1], s = 100, c = 'red', label = 'Cluster 1') # cluster 1
plt.scatter(newData[y_hc == 1, 0], newData[y_hc == 1, 1], s = 100, c = 'blue', label = 'Cluster 2') # cluster 2
plt.scatter(newData[y_hc == 2, 0], newData[y_hc == 2, 1], s = 100, c = 'green', label = 'Cluster 3') # cluster 3
plt.scatter(newData[y_hc == 3, 0], newData[y_hc == 3, 1], s = 100, c = 'cyan', label = 'Cluster 4') # cluster 4
plt.scatter(newData[y_hc == 4, 0], newData[y_hc == 4, 1], s = 100, c = 'magenta', label = 'Cluster 5') # cluster 5
plt.title('Clusters of customers')
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.legend()
plt.show()
如下:
关于层次聚类,我们需要了解的最后一个细节是它的时间和空间复杂是比较高的,因此不是解决大型数据集聚类问题的合适解决方案。
三、总结
加载全部内容