浅析Python是如何实现集合的

时间:2022-12-02 古明地觉人气:0

楔子

有几天没有更新 Python 文章了，本次我们来聊一下 Python 的集合是怎么实现的？之前我们介绍过字典的实现原理，它底层是基于哈希表实现的，而集合也是如此。

并且字典和集合实现的哈希表是一样的，在计算哈希值、解决索引冲突等方面，两者没有任何区别。唯一的区别就是存储的 entry 不同，字典的 entry 里面包含了 key、value 和 key 的哈希值，而集合的 entry 里面只包含 key 和 key 的哈希值。

事实上，集合就类似于没有value的字典。

集合的使用场景

那么集合都有哪些用处呢？

1）去重

chars = ["a", "b", "a", "c", "c"]

print(
    list(set(chars))
)  # ['b', 'a', 'c']

再比如你需要监听一个队列，处理接收到的消息，但每一条消息都有一个编号，要保证具有相同编号的消息只能被处理一次，要怎么做呢？

显然集合此时就派上用场了，我们可以创建一个集合，每来一条消息，就检测它的编号是否在集合中。如果存在，则说明消息已经被处理过了，忽略掉；如果不存在，说明消息还没有被处理，那么就将它的编号添加到集合中，然后处理消息。

这里暂时不考虑消费失败等情况，我们假设每条消息都是能处理成功的。

2）判断某个序列是否包含指定的多个元素

data = ["S", "A", "T", "O", "R", "I"]

# 现在要判断 data 是否包含 "T"、"R" 和 "I"
# 如果使用列表的话
print(
    "T" in data and "R" in data and "I" in data
)  # True

# 显然这是比较麻烦的，于是我们可以使用集合
print(
    set(data) >= {"T", "R", "I"}
)  # True

同理，基于此方式，我们也可以检测一个字典是否包含指定的多个 key。

data = {
    "name": "satori",
    "age": 17,
    "gender": "female"
}

# 判断字典是否包含 name、age、gender 三个 key
print(
    data.keys() >= {"name", "age", "gender"}
)  # True

# 字典的 keys 方法会返回一个 dict_keys 对象
# 该对象具备集合的性质，可以直接和集合进行运算

显然对于这种需求，有了集合就方便多了。

集合的 API

然后我们来罗列一下集合支持的 API，在使用集合的时候要做到心中有数。

# 如果要创建一个空集合，那么要使用 set()
# 写成 {} 的话，解释器会认为这是一个空字典
s = {1, 2, 3}

# 添加元素，时间复杂度是 O(1)
s.add(4)
print(s)  # {1, 2, 3, 4}

# 删除指定的元素，如果元素不存在则报出 KeyError
# 时间复杂度为 O(1)
s.remove(2)
print(s)  # {1, 3, 4}

# 删除指定的元素，如果元素不存在则什么也不做
# 时间复杂度为 O(1)
s.discard(666)
print(s)  # {1, 3, 4}

# 随机弹出一个元素并返回
# 时间复杂度为 O(1)
print(s.pop())  # 1
print(s)  # {3, 4}

# 清空一个集合
s.clear()
print(s)  # set()

# 还有一些 API，但我们更推荐使用操作符的方式
# 两个集合取交集
print({1, 2} & {2, 3})  # {2}

# 两个集合取并集
print({1, 2} | {2, 3})  # {1, 2, 3}

# 两个集合取差集
# s1 - s2，返回在 s1、但不在 s2 当中的元素
print({1, 2, 3} - {2, 3, 4})  # {1}

# 两个集合取对称差集
# s1 ^ s2，返回既不在 s1、也不在 s2 当中的元素
print({1, 2, 3} ^ {2, 3, 4})  # {1, 4}

# 判断两个集合是否相等，也就是内部的元素是否完全一致
# 顺序无所谓，只比较元素是否全部相同
print({1, 2, 3} == {3, 2, 1})  # True
print({1, 2, 3} == {1, 2, 4})  # False

# 判断一个集合是否包含另一个集合的所有元素
# 假设有两个集合 s1 和 s2：
#    如果 s1 的元素都在 s2 中，那么 s2 >= s1；
#    如果 s2 的元素都在 s1 中，那么 s1 >= s2；
#    如果 s1 和元素和 s2 全部相同，那么 s1 == s2；
print({1, 2, 3} > {1, 2})  # True
print({1, 2, 3} >= {1, 2, 3})  # True

以上就是集合支持的一些 API，还是很简单的，下面来重点看一下集合的底层结构。

集合的底层结构

集合的数据结构定义在 setobject.h 中，那么它长什么样子呢？

typedef struct {
    PyObject_HEAD
    Py_ssize_t fill;
    Py_ssize_t used;            
    Py_ssize_t mask;
    setentry *table;
    Py_hash_t hash;   
    Py_ssize_t finger;          
    setentry smalltable[PySet_MINSIZE];
    PyObject *weakreflist;    
} PySetObject;

解释一下这些字段的含义：

PyObject_HEAD：定长对象的头部信息，但集合显然是一个变长对象。所以和字典一样，肯定有其它字段充当 ob_size；
fill：等于 active 态的 entry 数量加上 dummy 态的 entry 数量。和字典类似，一个 entry 就是哈希表里面的一个元素，类型为 setentry，因此在集合里面一个 entry 就是一个 setentry 结构体实例；
used：等于 active 态的 entry 数量，显然这个 used 充当了 ob_size，也就是集合的元素个数；
mask：在看字典源码的时候，我们也见到了 mask，它用于和哈希值进行按位与、计算索引，并且这个 mask 等于哈希表的容量减 1，为什么呢？假设哈希值等于 v，哈希表容量是 n，那么通过 v 对 n 取模即可得到一个位于 0 到 n-1 之间的数。但是取模运算的效率不高，而 v&(n-1) 的作用等价于 v%n，并且速度更快，所以 mask 的值要等于哈希表的容量减 1。但是注意，只有在 n 为 2 的幂次方的时候， v&(n-1) 和 v%n 才是完全等价的，所以哈希表的容量要求是 2 的幂次方，就是为了将取模运算优化成按位与运算。
table：指向 setentry 数组的指针，而这个 setentry 数组可以是下面的 smalltable，也可以是单独申请的一块内存；
hash：集合的哈希值，只适用于不可变集合；
finger：用于 pop 一个元素；
smalltable：一个 setentry 类型的数组，集合的元素就存在里面。但我们知道，变长对象的内部不会存储具体元素，而是会存储一个指针，该指针指向的内存区域才是用来存储具体元素的。这样当扩容的时候，只需要让指针指向新的内存区域即可，从而方便维护。没错，对于集合而言，只有在容量不超过 8 的时候，元素才会存在里面；而一旦超过了8，那么会使用 malloc 单独申请内存；
weakreflist：弱引用列表，不做深入讨论；

有了字典的经验，再看集合会简单很多。然后是 setentry，用于承载集合内的元素，那么它的结构长什么样呢？相信你能够猜到。

typedef struct {
    PyObject *key; 
    Py_hash_t hash;
} setentry;

相比字典少了一个 value，这是显而易见的。因此集合的结构很清晰了，假设有一个集合 {3.14, "abc", 666}，那么它的结构如下：

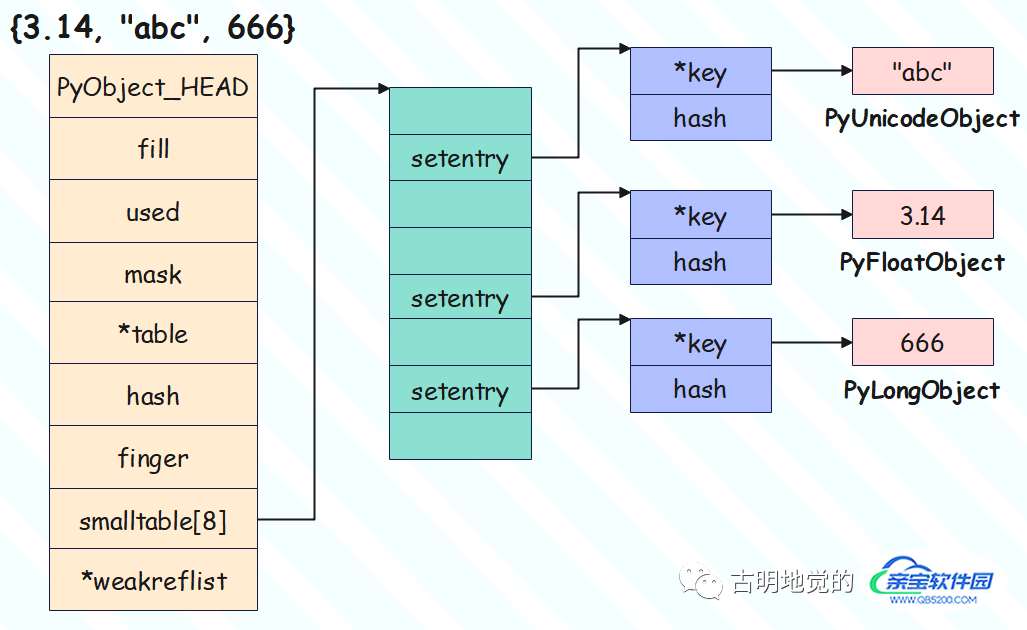
由于集合里面只有三个元素，所以它们都会存在 smalltable 数组里面，我们通过 ctypes 来证明这一点。

from ctypes import *

class PyObject(Structure):
    _fields_ = [
        ("ob_refcnt", c_ssize_t),
        ("ob_type", c_void_p),
    ]

class SetEntry(Structure):
    _fields_ = [
        ("key", POINTER(PyObject)),
        ("hash", c_longlong)
    ]

class PySetObject(PyObject):
    _fields_ = [
        ("fill", c_ssize_t),
        ("used", c_ssize_t),
        ("mask", c_ssize_t),
        ("table", POINTER(SetEntry)),
        ("hash", c_long),
        ("finger", c_ssize_t),
        ("smalltable", (SetEntry * 8)),
        ("weakreflist", POINTER(PyObject)),
    ]


s = {3.14, "abc", 666}
# 先来打印一下哈希值
print('hash(3.14) =', hash(3.14))
print('hash("abc") =', hash("abc"))
print('hash(666) =', hash(666))
"""
hash(3.14) = 322818021289917443
hash("abc") = 8036038346376407734
hash(666) = 666
"""

# 获取PySetObject结构体实例
py_set_obj = PySetObject.from_address(id(s))
# 遍历smalltable，打印索引、和哈希值
for index, entry in enumerate(py_set_obj.smalltable):
    print(index, entry.hash)
"""
0 0
1 0
2 666
3 322818021289917443
4 0
5 0
6 8036038346376407734
7 0
"""

根据输出的哈希值我们可以断定，这三个元素确实存在了 smalltable 数组里面，并且 666 存在了数组索引为 2 的位置、3.14 存在了数组索引为 3 的位置、"abc" 存在了数组索引为 6 的位置。

当然，由于哈希值是随机的，所以每次执行之后打印的结果都可能不一样，但是整数除外，它的哈希值就是它本身。既然哈希值不一样，那么每次映射出的索引也可能不同，但总之这三个元素是存在 smalltable 数组里面的。

然后我们再考察一下其它的字段：

s = {3.14, "abc", 666}
py_set_obj = PySetObject.from_address(id(s))
# 集合里面有 3 个元素，所以 fill 和 used 都是 3
print(py_set_obj.fill)  # 3
print(py_set_obj.used)  # 3

# 将集合元素全部删除
# 这里不能用 s.clear()，原因一会儿说
for _ in range(len(s)):
    s.pop()
    
# 我们知道哈希表在删除元素的时候是伪删除
# 所以 fill 不变，但是 used 每次会减 1
print(py_set_obj.fill)  # 3
print(py_set_obj.used)  # 0

fill 成员维护的是 active 态的 entry 数量加上 dummy 态的 entry 数量，所以删除元素时它的大小是不变的；但 used 成员的值每次会减 1，因为它维护的是 active 态的 entry 的数量。所以只要不涉及元素的删除，那么这两者的大小是相等的。

然后我们上面说不能用 s.clear()，因为该方法表示清空集合，此时会重置为初始状态，然后 fill 和 used 都会是 0，我们就观察不到想要的现象了。

删除集合所有元素之后，我们再往里面添加元素，看看是什么效果：

s = {3.14, "abc", 666}
py_set_obj = PySetObject.from_address(id(s))
for _ in range(len(s)):
    s.pop()

# 添加一个元素
s.add(0)
print(py_set_obj.fill)  # 3
print(py_set_obj.used)  # 1

多次执行的话，会发现打印的结果可能是 3、1，也有可能是 4、1。至于原因，有了字典的经验，相信你肯定能猜到。

首先添加元素之后，used 肯定为 1。至于 fill，如果添加元素的时候，正好撞上了一个 dummy 态的 entry，那么将其替换掉，此时 fill 不变，仍然是 3；如果没有撞上 dummy 态的 entry，而是添加在了新的位置，那么 fill 就是 4。

for i in range(1, 10):
    s.add(i)
print(py_set_obj.fill)  # 10
print(py_set_obj.used)  # 10
s.pop()
print(py_set_obj.fill)  # 10
print(py_set_obj.used)  # 9

在之前代码的基础上，继续添加 9 个元素，然后 used 变成了10，这很好理解，因为此时集合有 10 个元素。但 fill 也是10，这是为什么？很简单，因为哈希表扩容了，扩容时会删除 dummy 态的 entry，所以 fill 和 used 是相等的。同理，如果再继续 pop，那么 fill 和 used 就又变得不相等了。

集合的创建

集合的结构我们已经清楚了，再来看看它的初始化过程。我们调用类 set，传入一个可迭代对象，便可创建一个集合，这个过程是怎样的呢？

PyObject *
PySet_New(PyObject *iterable)
{  
    //底层调用了make_new_set
    return make_new_set(&PySet_Type, iterable);
}

底层提供了PySet_New函数用于创建一个集合，接收一个可迭代对象，然后调用 make_new_set 进行创建。

static PyObject *
make_new_set(PyTypeObject *type, PyObject *iterable)
{  
    // PySetObject *指针
    PySetObject *so;
  
    // 申请集合所需要的内存
    so = (PySetObject *)type->tp_alloc(type, 0);
    //申请失败，返回 NULL
    if (so == NULL)
        return NULL;
  
    // fill 和 used 初始都为 0
    so->fill = 0;
    so->used = 0;
    // PySet_MINSIZE 默认为 8
    // 而 mask 等于哈希表容量减 1，所以初始值是 7
    so->mask = PySet_MINSIZE - 1;
    // 初始化的时候，setentry 数组显然是 smalltable
    // 所以让 table 指向 smalltable 数组
    so->table = so->smalltable;
    // 初始 hash 值为 -1
    so->hash = -1;
    // finger为0
    so->finger = 0;
    // 弱引用列表为NULL
    so->weakreflist = NULL;
    //以上只是初始化，如果可迭代对象不为 NULL
    //那么把元素依次设置到集合中
    if (iterable != NULL) {
    //该过程是通过 set_update_internal 函数实现的
    //该函数内部会遍历 iterable，将迭代出的元素依次添加到集合里面
        if (set_update_internal(so, iterable)) {
            Py_DECREF(so);
            return NULL;
        }
    }
    //返回初始化完成的set
    return (PyObject *)so;
}

整个过程没什么难度，非常好理解。

小结

以上就是集合相关的内容，它的效率也是非常高的，能够以O(1)的复杂度去查找某个元素。最关键的是，它用起来也特别的方便。

此外 Python 里面还有一个 frozenset，也就是不可变的集合。但 frozenset 对象和 set 对象都是同一个结构体，只有 PySetObject，没有 PyFrozenSetObject。

我们在看 PySetObject的时候，发现该对象里面也有个 hash 成员，如果是不可变集合，那么 hash 值是不为 -1 的，因为它不可以添加、删除元素，是不可变对象。

加载全部内容