matplotlib 多子图绘制
王小王-123 人气:0简单了解多子图
学习matplotlib的时候,有人肯定会觉得为啥不用Excel,为啥不用origin,为啥不直接使用软件,其实matplotlib绘图之所以在python领域经久不衰,是有它的独特之处的,我认为这其中的一个亮点就是,matplotlib绘制多个子图的时候,我们可以根据自己的想法去排列子图的顺序,也可以生成不同的子图数量,类似于前端web可视化大屏,有着较好的用户体验感!

使用plt.subplot(mnx) 分别绘制
# -*- coding: utf-8 -*-
import matplotlib as mpl
import matplotlib.pyplot as plt
t=np.arange(0.0,2.0,0.1)
s=np.sin(t*np.pi)
plt.subplot(2,2,1) #要生成两行两列,这是第一个图
plt.plot(t,s,'b*')
plt.ylabel('y1')
plt.subplot(2,2,2) #两行两列,这是第二个图
plt.plot(2*t,s,'r--')
plt.ylabel('y2')
plt.subplot(2,2,3)#两行两列,这是第三个图
plt.plot(3*t,s,'m--')
plt.ylabel('y3')
plt.subplot(2,2,4)#两行两列,这是第四个图
plt.plot(4*t,s,'k*')
plt.ylabel('y4')
plt.show()
使用plt.subplot()方法,生成子图,规则总结如下:
第一个数字是行,第二个数字是列,第三个数字是个数(图形所处顺序的序号)
例如:224就是生成两行两列的子图,本图形是第四个,那么就是第二行第二列的图形
那么有时候,有些人觉得这样太麻烦了,每次生成都要在绘图程序前面加一行这样的代码,为什么不可以一次性生成我需要的画布呢?答案是可以的!
使用plt.subplots(m,n),可以一次性生成m行n列的字图
注意前面需要figure和ax进行接收
调用就和我们数组一样!
使用plt.subplots(m,n)一次性绘制
# -*- coding: utf-8 -*- import matplotlib as mpl import matplotlib.pyplot as plt t=np.arange(0.0,2.0,0.1) s=np.sin(t*np.pi) c=np.cos(t*np.pi) figure,ax=plt.subplots(2,2) # 多行subplots得到的ax数组是二维的 ax[0][0].plot(t,s,'r*') ax[0][1].plot(t*2,s,'b--') ax[1][0].plot(t,c,'g*') ax[1][1].plot(t*2,c,'y--')

# -*- coding: utf-8 -*- import matplotlib as mpl import matplotlib.pyplot as plt import numpy as np t=np.arange(0.0,2.0,0.1) s=np.sin(t*np.pi) c=np.cos(t*np.pi) figure,ax=plt.subplots(1,2,figsize=(6,2),dpi=120) # 一行subplots得到的ax数组是一维的 ax[0].plot(t,s,'r*') ax[1].plot(t*2,s,'b--')
plt.subplots(nrows=1,ncols=3,figsize=(5,5)) #plt.subplots(nrows=1,ncols=3) # 返回一个figure对象,和一个axesSubplot子图对象的数组 # 行或者列等于1,返回一个一维数组
加一个plt.tight_layout()会使得图形更加紧凑
plt.tight_layout() plt.subplots(nrows=2,ncols=3, figsize=(12,8)) # 如果行列都不为1,那么返回一个2维数组
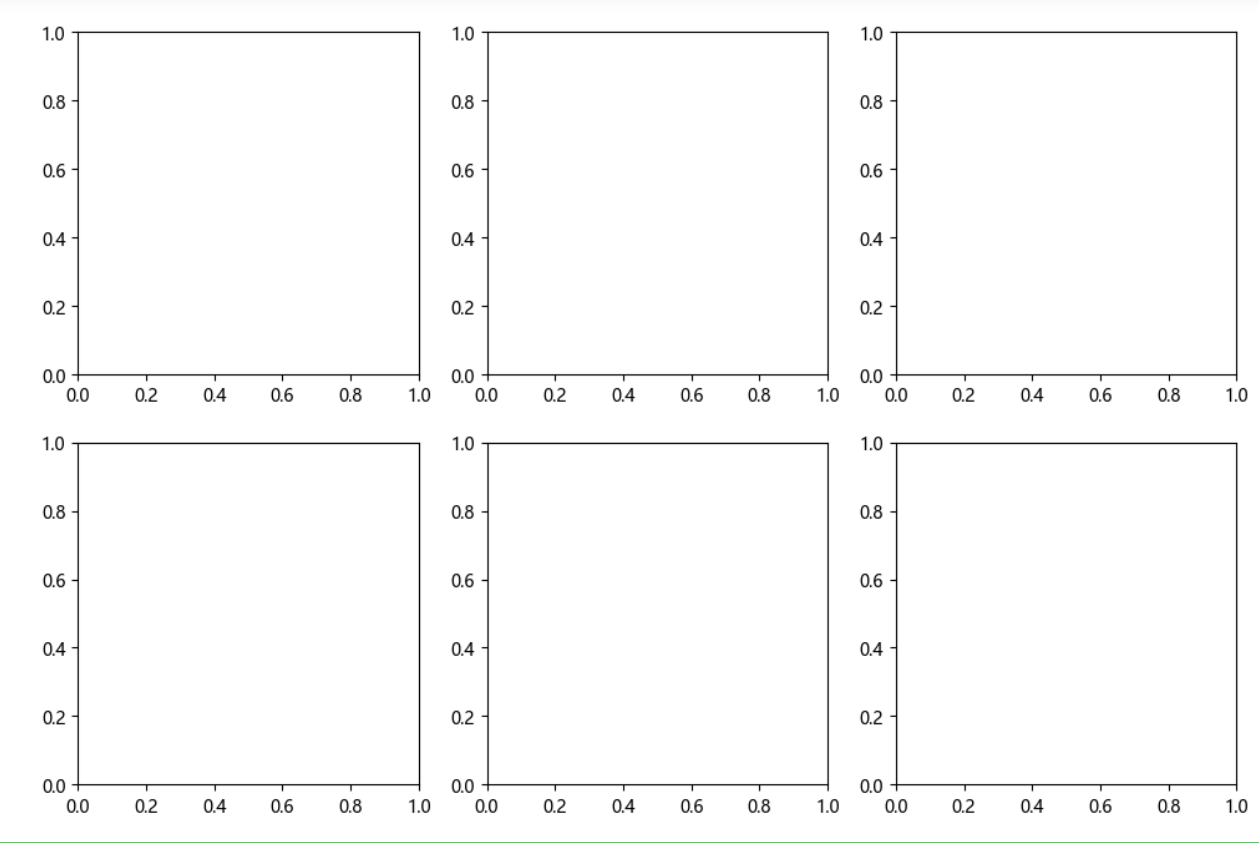
plt.subplots(nrows=3,ncols=4) # 如果行和列都大于1,返回1个Figure对象,和1个包含3*4=12个子图对象的矩阵(2维数组) # 341 342 343 344 # 345 346 347 348 # 349 3,4,10 3,4,11 3,4,12

高级进阶
plt.subplot(121) plt.subplot(222) plt.subplot(224)
看到上面你会想到什么?会生成怎样的画布呢?

下面我就给大家详细的解释一下,为啥会出现这样的画布,首先我的需求是在左边出现一个子图,比较长的,最好是右边两个子图的长度和,那么应该怎么做呢?遇到这样的情况我们仍然需要把这一个平面分成均等分,那么也就是四个。
当我们画一个左边的图的时候,我们应该把画布想象为一行两列的画布,第一个自然也就是121
当我们画右边的图形的时候,我们应该把画布想象为两行两列的画布,右边第一个自然就是222,第二个自然就是224。
下面我们可以多看几个,来验证我们得推论
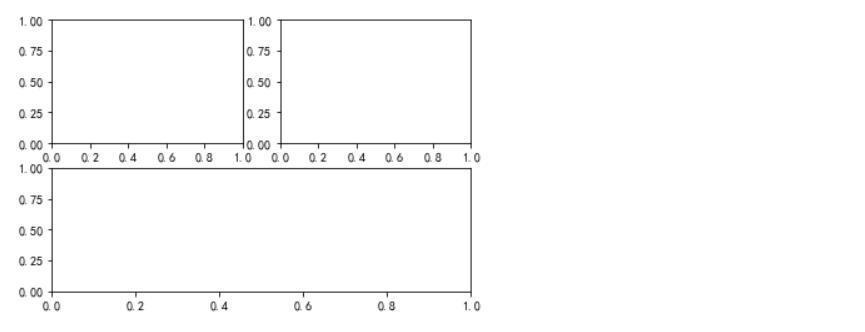
plt.subplot(221) plt.subplot(223) plt.subplot(122)

plt.subplot(211) plt.subplot(223) plt.subplot(224)
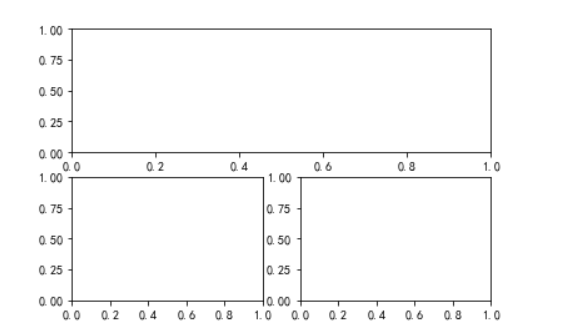
plt.subplot(221) plt.subplot(222) plt.subplot(212)
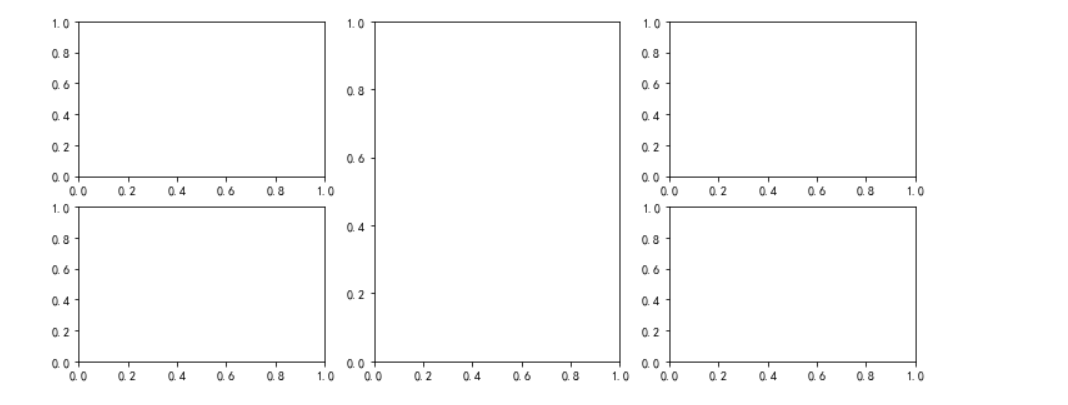
plt.figure(figsize=(12,5)) plt.subplot(231) plt.subplot(233) plt.subplot(234) plt.subplot(236) plt.subplot(132)
plt.figure(figsize=(16,5)) plt.subplot(262) plt.subplot(265) plt.subplot(268) plt.subplot(2,6,11) plt.subplot(132)

注意这个间隙是自动产生的,如果需要将间隙变的更大,那么就可以取最左边的值和最右边的值
plt.figure(figsize=(16,5)) plt.subplot(241) plt.subplot(244) plt.subplot(245) plt.subplot(2,4,8) plt.subplot(132)
总结
在生成上面案例的时候,我们需要利用Excel进行编排,不然很容易出错的!
加载全部内容