R语言检验数据缺失类型 R语言刷题检验数据缺失类型过程详解
Kanny广小隶 人气:0题目


解答
由于题目要求需要重复三次类似的操作,故首先载入所需要的包,构造生成数据的函数以及绘图的函数:
library(tidyr) # 绘图所需
library(ggplot2) # 绘图所需
# 生成数据
GenerateData <- function(a = 0, b = 0, seed = 2018) {
set.seed(seed)
z1 <- rnorm(100)
z2 <- rnorm(100)
z3 <- rnorm(100)
y1 <- 1 + z1
y2 <- 5 + 2 * z1 + z2
u <- a * (y1 - 1) + b * (y2 - 5) + z3
m2 <- 1 * (u < 0)
y2_na <- y2
y2_na[u < 0] <- NA
# y2_na[as.logical(m2)] <- NA
dat_comp <- data.frame(y1 = y1, y2 = y2)
dat_incomp <- data.frame(y1 = y1, y2 = y2_na)
dat_incomp <- na.omit(dat_incomp)
return(list(dat_comp = dat_comp, dat_incomp = dat_incomp))
}
# 展现缺失出具与未缺失数据的分布情况
PlotTwoDistribution <- function(dat) {
p1 <- dat_comp %>%
gather(y1, y2, key = "var", value = "value") %>%
ggplot(aes(x = value)) +
geom_histogram(aes(fill = factor(var), y = ..density..),
alpha = 0.3, colour = 'black') +
stat_density(geom = 'line', position = 'identity', size = 1.5,
aes(colour = factor(var))) +
facet_wrap(~ var, ncol = 2) +
labs(y = '直方图与密度曲线', x = '值',
title = '完整无缺失数据', fill = '变量') +
theme(plot.title = element_text(hjust = 0.5)) +
guides(color = FALSE)
p2 <- dat_incomp %>%
gather(y1, y2, key = "var", value = "value") %>%
ggplot(aes(x = value)) +
geom_histogram(aes(fill = factor(var), y = ..density..),
alpha = 0.3, colour = 'black') +
stat_density(geom = 'line', position = 'identity', size = 1.5,
aes(colour = factor(var))) +
facet_wrap(~ var, ncol = 2) +
labs(y = '直方图与密度曲线', x = '值',
title = '有缺失数据', fill = '变量') +
theme(plot.title = element_text(hjust = 0.5)) +
guides(color = FALSE)
return(list(p_comp = p1, p_incomp = p2))
}
下面考虑三种情况:
1. a = 0, b = 0
a) 生成数据并绘图展示
# 生成数据并查看数据样式 dat <- GenerateData(a = 0, b = 0) dat_comp <- dat$dat_comp dat_incomp <- dat$dat_incomp head(dat_comp) head(dat_incomp)
# 绘图展示 p <- PlotTwoDistribution(dat) p$p_comp p$p_incomp
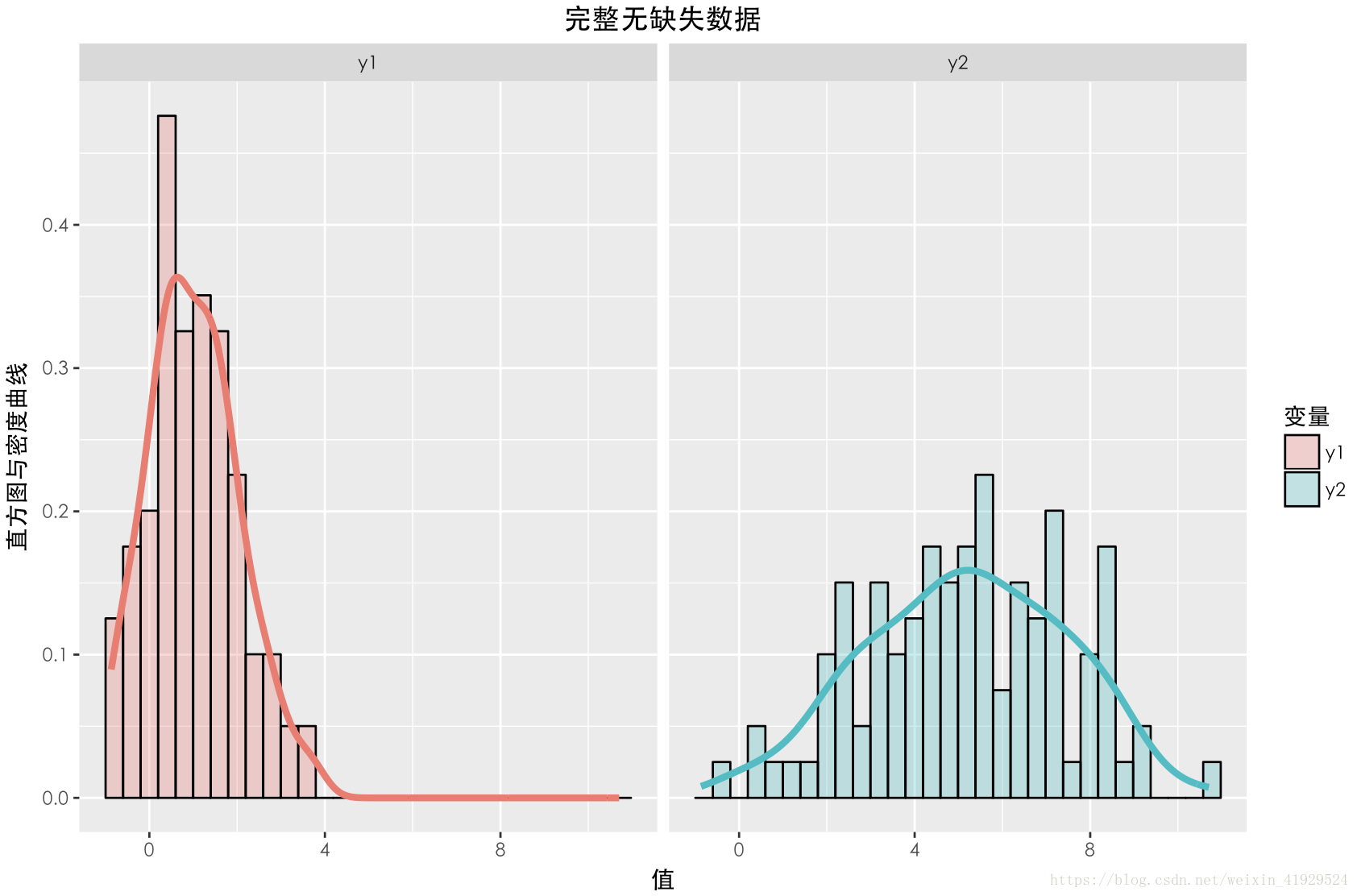
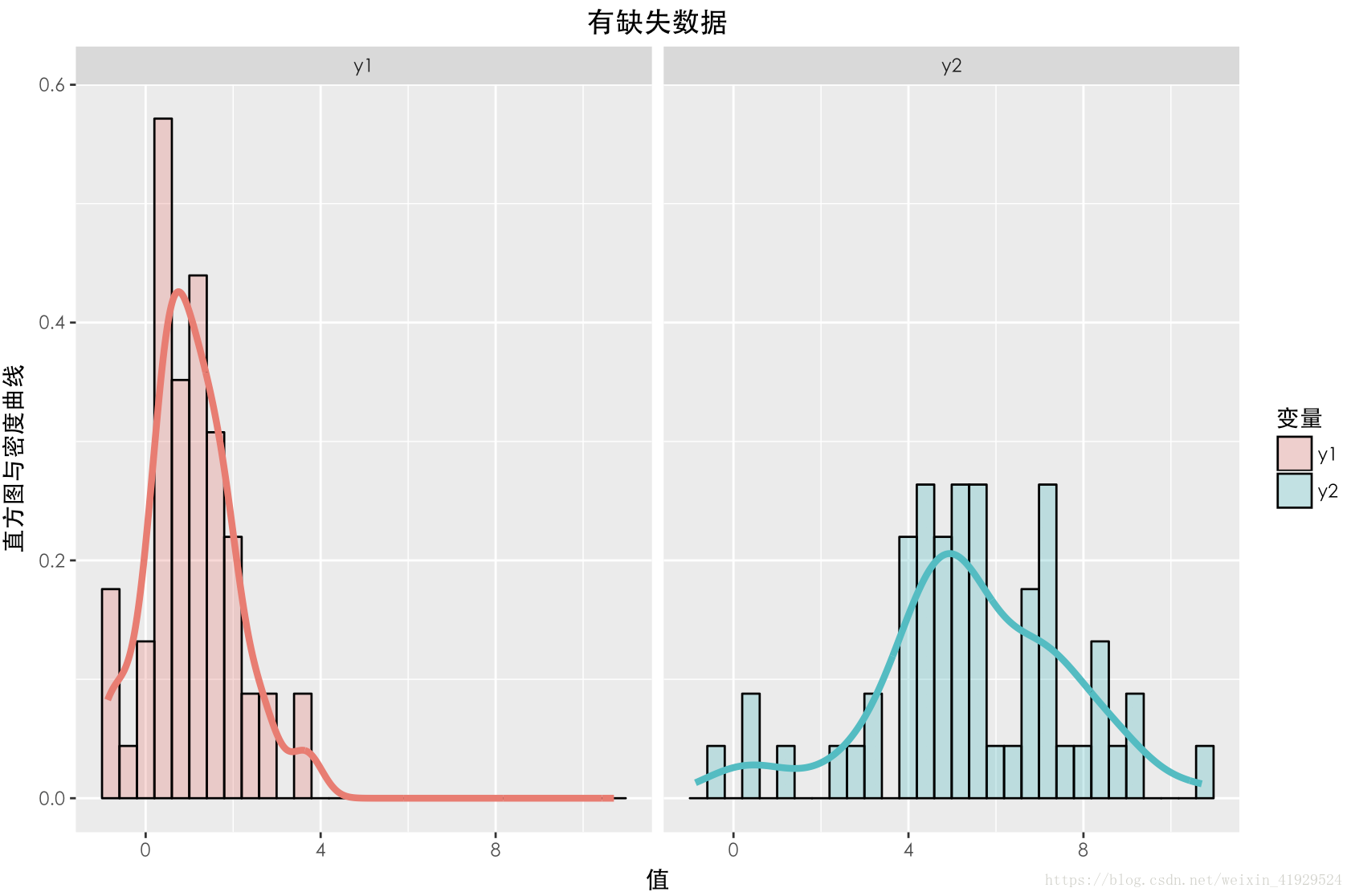
缺失数据与未缺失数据的分布如上图所示。可以发现,对于完整数据与缺失数据之间的 Y1的分布与 Y2的分布与期望相差不大。并且在采用 a=0,b=0这种构造时,从构造的公式可以看出, Y2中样本的缺失情况与 Y1,Y2两者都无关(因为 Z 3 与 Y 1 , Y 2 均独立),所以这种缺失机制是:MCAR。
b) 进行t检验
题设条件中说的是 Y1的均值,所以考虑完整数据与缺失数据(这里的缺失指的是若 Y2有缺失,Y1也会进行相应地缺失处理)
t.test(dat_comp$y1, dat_incomp$y1)
这里进行t检验(其实不是非常严谨,因为不一定满足正态假设),比较缺失与否 Y1的均值,这里p-value = 0.8334。在显著性水平为0.05的前提下,并不能断言有缺失与无缺失两个Y1之间的均值有差异,也就是说其实MCAR, MAR, NMAR三种情况都有可能,并不能断言哪种不可能发生。
2. a = 2, b = 0
a) 生成数据并绘图展示
# 生成数据并查看数据样式 dat <- GenerateData(a = 2, b = 0) dat_comp <- dat$dat_comp dat_incomp <- dat$dat_incomp head(dat_comp) head(dat_incomp)
# 绘图展示 p <- PlotTwoDistribution(dat) p$p_comp p$p_incomp
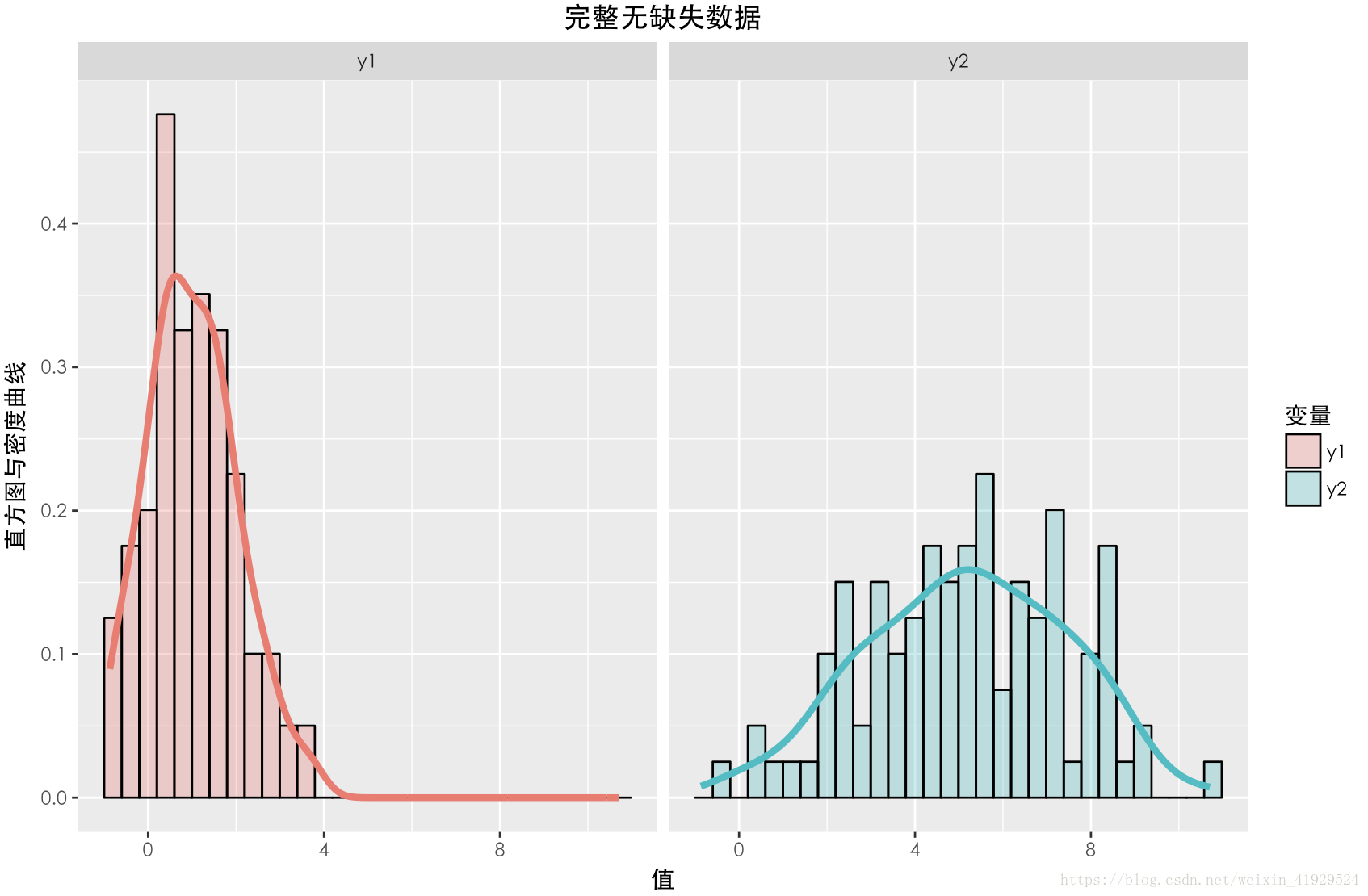
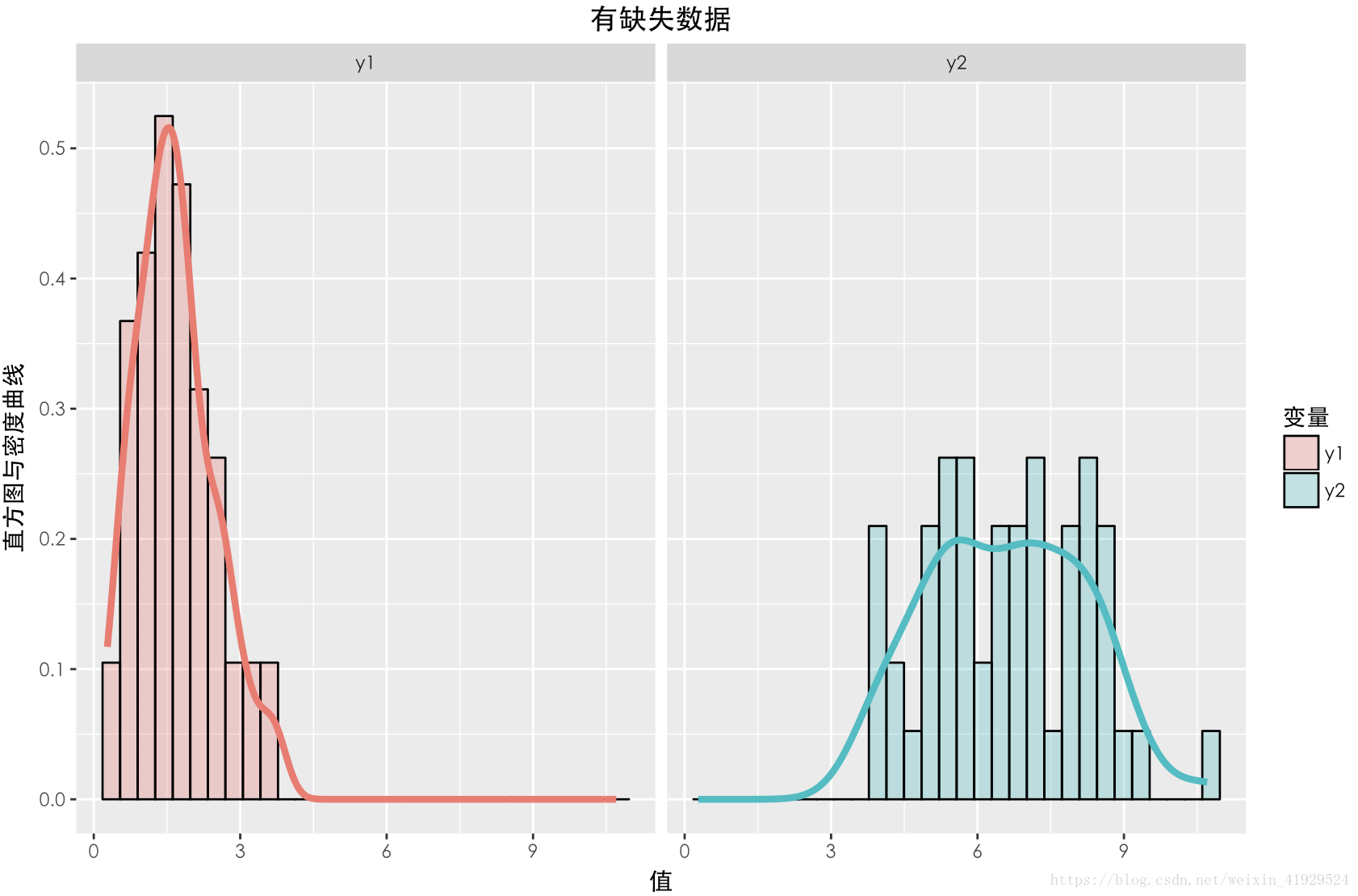
缺失数据与未缺失数据的分布如上图所示。可以发现,两个数据的期望以及分布(无论 Y1还是 Y2),整体都有一定差异。在采用 a = 2 , b = 0 这种构造时,从构造的公式可以看出, Y2中样本的缺失情况与 Y1有关,所以这种缺失机制是:MAR。
b) 进行t检验
t.test(dat_comp$y1, dat_incomp$y1)

3. a = 0, b = 2
a) 生成数据并绘图展示
# 生成数据并查看数据样式 dat <- GenerateData(a = 0, b = 2) dat_comp <- dat$dat_comp dat_incomp <- dat$dat_incomp head(dat_comp) head(dat_incomp)
# 绘图展示 p <- PlotTwoDistribution(dat) p$p_comp p$p_incomp
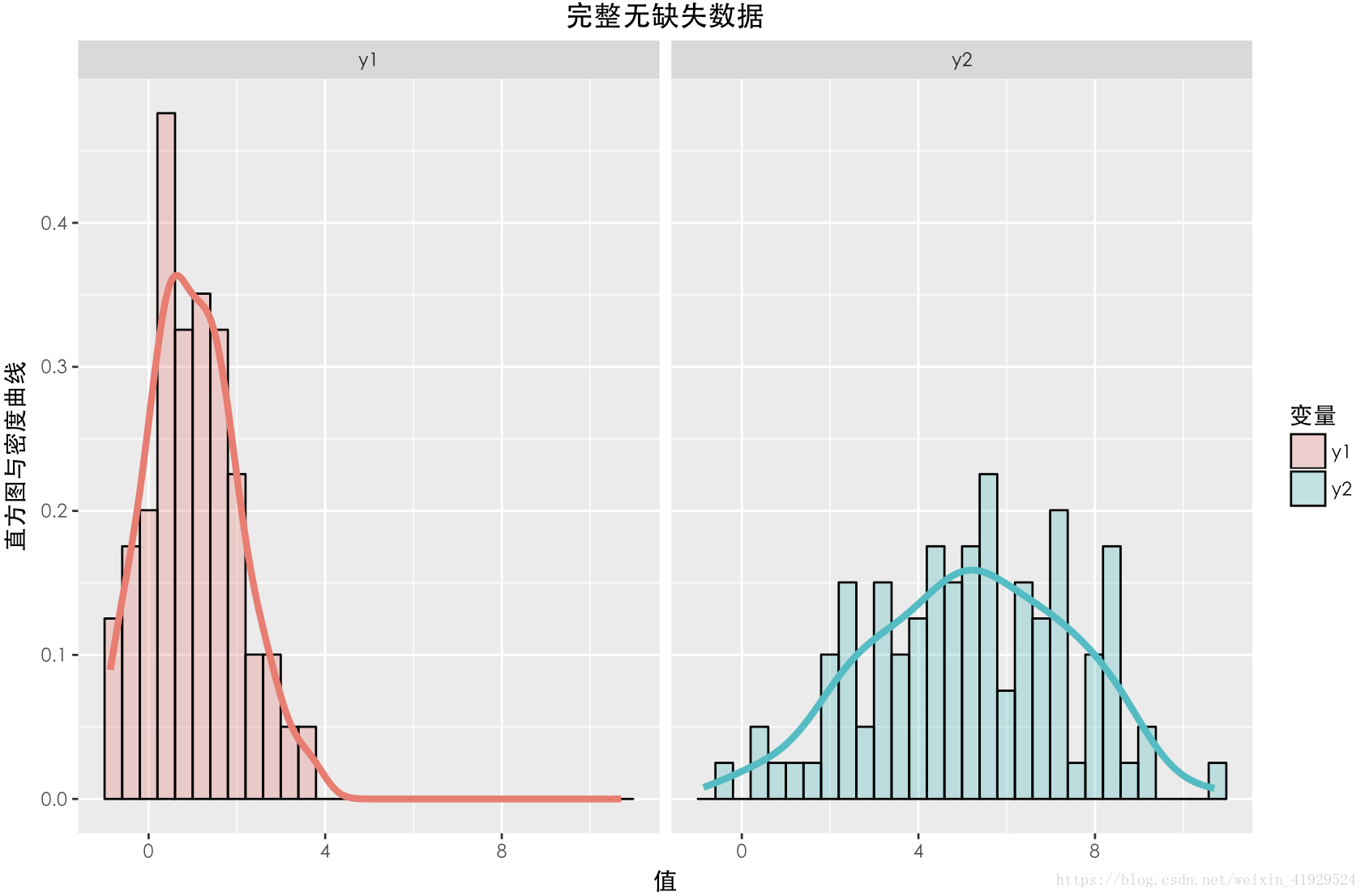

缺失数据与未缺失数据的分布如上图所示。可以发现与上一种情况一样,两个数据的期望以及分布(无论 Y1还是 Y2),整体都有一定差异。在采用 a = 0 , b = 2 这种构造时,从构造的公式可以看出,Y2中样本的缺失情况与 Y2本身有关,所以这种缺失机制是:NMAR。
b) 进行t检验
t.test(dat_comp$y1, dat_incomp$y1)

加载全部内容