R绘图输出希腊字符上下标及数学公式 R语言绘图时输出希腊字符上下标及数学公式实现方法
Kanny广小隶 人气:0想了解R语言绘图时输出希腊字符上下标及数学公式实现方法的相关内容吗,Kanny广小隶在本文为您仔细讲解R绘图输出希腊字符上下标及数学公式的相关知识和一些Code实例,欢迎阅读和指正,我们先划重点:R绘图时输出希腊字符,R绘图输出上下标,R绘图输出数学公式,下面大家一起来学习吧。
通常在我们写论文时,所需要的统计图是非常严谨的,里面的希腊字符与上下脚标都必须要严格书写。因此在使用R绘图时,如何在我们目标图中使用希腊字符、上标、下标及一些数学公式呢?在本博客中我们会进行详细的说明。
后面我们都将以一个最简单的绘图为例,只是将其标题进行修改。
希腊字母
使用希腊字符、上标、下标及数学公式,都需要利用一个函数:expression(),具体使用方式如下:
plot(cars) title(main = expression(Sigma))
输出:

上下标
expression()中的下标为[],上标为^,空格为~,连接符为*。示例代码如下:
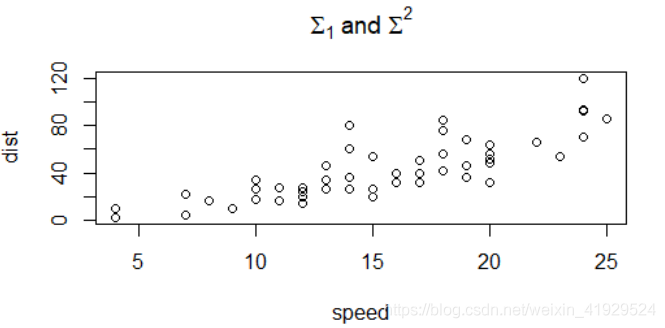
plot(cars) title(main = expression(Sigma[1]~'a'*'n'*'d'~Sigma^2))
输出:
paste
想达到上面的效果,我们其实可以使用paste()与expression()进行组合,不需要上述繁琐的过程,也能够达到我们上述一模一样的输出,并且方便快捷:
plot(cars) title(main = expression(paste(Sigma[1], ' and ', Sigma^2)))
一个复杂的例子
目标:
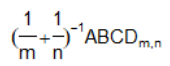
代码:
expression(paste((frac(1, m)+frac(1, n))^-1, ABCD[paste(m, ',', n)]))
进阶
在我们想批量产生大量含有不同变量值的标题时,如果遇到变量与公式的混合输出该如何操作,
可参考前文:R语言绘图公式与变量对象混合拼接实现方法
数学公式
最后的数学公式,只需要在expression()中进行相应的符号连接即可
具体要求可参考:Mathematical Annotation in R
鉴于其很不稳定,这里将里面的细节搬运过来。
(下表也可以直接在 R help 中搜索 plotmath 获取。)
| Syntax | Meaning |
|---|---|
| x + y | x plus y |
| x - y | x minus y |
| x*y | juxtapose x and y |
| x/y | x forwardslash y |
| x %±% y | x plus or minus y |
| x %/% y | x divided by y |
| x %*% y | x times y |
| x %.% y | x cdot y |
| x[i] | x subscript i |
| x^2 | x superscript 2 |
| paste(x, y, z) | juxtapose x, y, and z |
| sqrt(x) | square root of x |
| sqrt(x, y) | yth root of x |
| x == y | x equals y |
| x != y | x is not equal to y |
| x < y | x is less than y |
| x <= y | x is less than or equal to y |
| x > y | x is greater than y |
| x >= y | x is greater than or equal to y |
| !x | not x |
| x %~~% y | x is approximately equal to y |
| x %=~% y | x and y are congruent |
| x %==% y | x is defined as y |
| x %prop% y | x is proportional to y |
| x %~% y | x is distributed as y |
| plain(x) | draw x in normal font |
| bold(x) | draw x in bold font |
| italic(x) | draw x in italic font |
| bolditalic(x) | draw x in bolditalic font |
| symbol(x) | draw x in symbol font |
| list(x, y, z) | comma-separated list |
| … | ellipsis (height varies) |
| cdots | ellipsis (vertically centred) |
| ldots | ellipsis (at baseline) |
| x %subset% y | x is a proper subset of y |
| x %subseteq% y | x is a subset of y |
| x %notsubset% y | x is not a subset of y |
| x %supset% y | x is a proper superset of y |
| x %supseteq% y | x is a superset of y |
| x %in% y | x is an element of y |
| x %notin% y | x is not an element of y |
| hat(x) | x with a circumflex |
| tilde(x) | x with a tilde |
| dot(x) | x with a dot |
| ring(x) | x with a ring |
| bar(xy) | xy with bar |
| widehat(xy) | xy with a wide circumflex |
| widetilde(xy) | xy with a wide tilde |
| x %<->% y | x double-arrow y |
| x %->% y | x right-arrow y |
| x %<-% y | x left-arrow y |
| x %up% y | x up-arrow y |
| x %down% y | x down-arrow y |
| x %<=>% y | x is equivalent to y |
| x %=>% y | x implies y |
| x %<=% y | y implies x |
| x %dblup% y | x double-up-arrow y |
| x %dbldown% y | x double-down-arrow y |
| alpha – omega | Greek symbols |
| Alpha – Omega | uppercase Greek symbols |
| theta1, phi1, sigma1, omega1 | cursive Greek symbols |
| Upsilon1 | capital upsilon with hook |
| aleph | first letter of Hebrew alphabet |
| infinity | infinity symbol |
| partialdiff | partial differential symbol |
| nabla | nabla, gradient symbol |
| 32*degree | 32 degrees |
| 60*minute | 60 minutes of angle |
| 30*second | 30 seconds of angle |
| displaystyle(x) | draw x in normal size (extra spacing) |
| textstyle(x) | draw x in normal size |
| scriptstyle(x) | draw x in small size |
| scriptscriptstyle(x) | draw x in very small size |
| underline(x) | draw x underlined |
| x ~~ y | put extra space between x and y |
| x + phantom(0) + y | leave gap for “0”, but don't draw it |
| x + over(1, phantom(0)) | leave vertical gap for “0” (don't draw) |
| frac(x, y) | x over y |
| over(x, y) | x over y |
| atop(x, y) | x over y (no horizontal bar) |
| sum(x[i], i==1, n) | sum x[i] for i equals 1 to n |
| prod(plain§(X==x), x) | product of P(X=x) for all values of x |
| integral(f(x)*dx, a, b) | definite integral of f(x) wrt x |
| union(A[i], i==1, n) | union of A[i] for i equals 1 to n |
| intersect(A[i], i==1, n) | intersection of A[i] |
| lim(f(x), x %->% 0) | limit of f(x) as x tends to 0 |
| min(g(x), x > 0) | minimum of g(x) for x greater than 0 |
| inf(S) | infimum of S |
| sup(S) | supremum of S |
| x^y + z | normal operator precedence |
| x^(y + z) | visible grouping of operands |
| x^{y + z} | invisible grouping of operands |
| group("(",list(a, b),"]") | specify left and right delimiters |
| bgroup("(",atop(x,y),")") | use scalable delimiters |
| group(lceil, x, rceil) | special delimiters |
| group(lfloor, x, rfloor) | special delimiters |
加载全部内容