C语言计算矩阵乘法 C语言科学计算入门之矩阵乘法的相关计算
Denlee 人气:01.矩阵相乘
矩阵相乘应满足的条件:
(1) 矩阵A的列数必须等于矩阵B的行数,矩阵A与矩阵B才能相乘;
(2) 矩阵C的行数等于矩阵A的行数,矩阵C的列数等于矩阵B的列数;
(3) 矩阵C中第i行第j列的元素等于矩阵A的第i行元素与矩阵B的第j列元素对应乘积之和,即
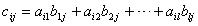
如:
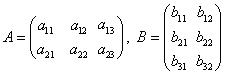
则:
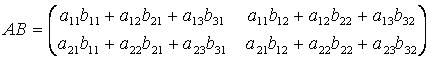
2. 常用矩阵相乘算法
用A的第i行分别和B的第j列的各个元素相乘求和,求得C的第i行j列的元素,这种算法中,B的访问是按列进行访问的,代码如下:
void arymul(int a[4][5], int b[5][3], int c[4][3])
{
int i, j, k;
int temp;
for(i = 0; i < 4; i++){
for(j = 0; j < 3; j++){
temp = 0;
for(k = 0; k < 5; k++){
temp += a[i][k] * b[k][j];
}
c[i][j] = temp;
printf("%d/t", c[i][j]);
}
printf("%d/n");
}
}
3. 改进的算法
矩阵A、B、C都按行(数据的存储顺序)访问,以提高存储器访问效率,对于A的第i行中,第j列的元素分别和B的第j行的元素相乘,对于B中相同的列k在上述计算过程中求和,从而得到C第i行k列的数据,代码如下:
void arymul1(int a[4][5], int b[5][3], int c[4][3])
{
int i, j, k;
int temp[3] = {0};
for(i = 0; i < 4; i++){
for(k = 0; k < 3; k ++)
temp[k] = 0;
for(j = 0; j < 5; j++){//当前行的每个元素
for(k = 0; k < 3; k++){
temp[k] += a[i][j] * b[j][k];
}
}
for(k = 0; k < 3; k++){
c[i][k] = temp[k];
printf("%d/t", c[i][k]);
}
printf("%d/n");
}
}
这种算法很容易转到稀疏矩阵的相乘算法。
PS:斯特拉森算法的实现
斯特拉森方法,是由v.斯特拉森在1969年提出的一个方法。
我们先讨论二阶矩阵的计算方法。
对于二阶矩阵
a11 a12 b11 b12 A = a21 a22 B = b21 b22
先计算下面7个量(1)
x1 = (a11 + a22) * (b11 + b22); x2 = (a21 + a22) * b11; x3 = a11 * (b12 - b22); x4 = a22 * (b21 - b11); x5 = (a11 + a12) * b22; x6 = (a21 - a11) * (b11 + b12); x7 = (a12 - a22) * (b21 + b22);
再设C = AB。根据矩阵相乘的规则,C的各元素为(2)
c11 = a11 * b11 + a12 * b21 c12 = a11 * b12 + a12 * b22 c21 = a21 * b11 + a22 * b21 c22 = a21 * b12 + a22 * b22
比较(1)(2),C的各元素可以表示为(3)
c11 = x1 + x4 - x5 + x7 c12 = x3 + x5 c21 = x2 + x4 c22 = x1 + x3 - x2 + x6
根据以上的方法,我们就可以计算4阶矩阵了,先将4阶矩阵A和B划分成四块2阶矩阵,分别利用公式计算它们的乘积,再使用(1)(3)来计算出最后结果。
ma11 ma12 mb11 mb12 A4 = ma21 ma22 B4 = mb21 mb22
其中
a11 a12 a13 a14 b11 b12 b13 b14 ma11 = a21 a22 ma12 = a23 a24 mb11 = b21 b22 mb12 = b23 b24 a31 a32 a33 a34 b31 b32 b33 b34 ma21 = a41 a42 ma22 = a43 a44 mb21 = b41 b42 mb22 = b43 b44
实现
// 计算2X2矩阵
void Multiply2X2(float& fOut_11, float& fOut_12, float& fOut_21, float& fOut_22,
float f1_11, float f1_12, float f1_21, float f1_22,
float f2_11, float f2_12, float f2_21, float f2_22)
{
const float x1((f1_11 + f1_22) * (f2_11 + f2_22));
const float x2((f1_21 + f1_22) * f2_11);
const float x3(f1_11 * (f2_12 - f2_22));
const float x4(f1_22 * (f2_21 - f2_11));
const float x5((f1_11 + f1_12) * f2_22);
const float x6((f1_21 - f1_11) * (f2_11 + f2_12));
const float x7((f1_12 - f1_22) * (f2_21 + f2_22));
fOut_11 = x1 + x4 - x5 + x7;
fOut_12 = x3 + x5;
fOut_21 = x2 + x4;
fOut_22 = x1 - x2 + x3 + x6;
}
// 计算4X4矩阵
void Multiply(CLAYMATRIX& mOut, const CLAYMATRIX& m1, const CLAYMATRIX& m2)
{
float fTmp[7][4];
// (ma11 + ma22) * (mb11 + mb22)
Multiply2X2(fTmp[0][0], fTmp[0][1], fTmp[0][2], fTmp[0][3],
m1._11 + m1._33, m1._12 + m1._34, m1._21 + m1._43, m1._22 + m1._44,
m2._11 + m2._33, m2._12 + m2._34, m2._21 + m2._43, m2._22 + m2._44);
// (ma21 + ma22) * mb11
Multiply2X2(fTmp[1][0], fTmp[1][1], fTmp[1][2], fTmp[1][3],
m1._31 + m1._33, m1._32 + m1._34, m1._41 + m1._43, m1._42 + m1._44,
m2._11, m2._12, m2._21, m2._22);
// ma11 * (mb12 - mb22)
Multiply2X2(fTmp[2][0], fTmp[2][1], fTmp[2][2], fTmp[2][3],
m1._11, m1._12, m1._21, m1._22,
m2._13 - m2._33, m2._14 - m2._34, m2._23 - m2._43, m2._24 - m2._44);
// ma22 * (mb21 - mb11)
Multiply2X2(fTmp[3][0], fTmp[3][1], fTmp[3][2], fTmp[3][3],
m1._33, m1._34, m1._43, m1._44,
m2._31 - m2._11, m2._32 - m2._12, m2._41 - m2._21, m2._42 - m2._22);
// (ma11 + ma12) * mb22
Multiply2X2(fTmp[4][0], fTmp[4][1], fTmp[4][2], fTmp[4][3],
m1._11 + m1._13, m1._12 + m1._14, m1._21 + m1._23, m1._22 + m1._24,
m2._33, m2._34, m2._43, m2._44);
// (ma21 - ma11) * (mb11 + mb12)
Multiply2X2(fTmp[5][0], fTmp[5][1], fTmp[5][2], fTmp[5][3],
m1._31 - m1._11, m1._32 - m1._12, m1._41 - m1._21, m1._42 - m1._22,
m2._11 + m2._13, m2._12 + m2._14, m2._21 + m2._23, m2._22 + m2._24);
// (ma12 - ma22) * (mb21 + mb22)
Multiply2X2(fTmp[6][0], fTmp[6][1], fTmp[6][2], fTmp[6][3],
m1._13 - m1._33, m1._14 - m1._34, m1._23 - m1._43, m1._24 - m1._44,
m2._31 + m2._33, m2._32 + m2._34, m2._41 + m2._43, m2._42 + m2._44);
// 第一块
mOut._11 = fTmp[0][0] + fTmp[3][0] - fTmp[4][0] + fTmp[6][0];
mOut._12 = fTmp[0][1] + fTmp[3][1] - fTmp[4][1] + fTmp[6][1];
mOut._21 = fTmp[0][2] + fTmp[3][2] - fTmp[4][2] + fTmp[6][2];
mOut._22 = fTmp[0][3] + fTmp[3][3] - fTmp[4][3] + fTmp[6][3];
// 第二块
mOut._13 = fTmp[2][0] + fTmp[4][0];
mOut._14 = fTmp[2][1] + fTmp[4][1];
mOut._23 = fTmp[2][2] + fTmp[4][2];
mOut._24 = fTmp[2][3] + fTmp[4][3];
// 第三块
mOut._31 = fTmp[1][0] + fTmp[3][0];
mOut._32 = fTmp[1][1] + fTmp[3][1];
mOut._41 = fTmp[1][2] + fTmp[3][2];
mOut._42 = fTmp[1][3] + fTmp[3][3];
// 第四块
mOut._33 = fTmp[0][0] - fTmp[1][0] + fTmp[2][0] + fTmp[5][0];
mOut._34 = fTmp[0][1] - fTmp[1][1] + fTmp[2][1] + fTmp[5][1];
mOut._43 = fTmp[0][2] - fTmp[1][2] + fTmp[2][2] + fTmp[5][2];
mOut._44 = fTmp[0][3] - fTmp[1][3] + fTmp[2][3] + fTmp[5][3];
}
比较
在标准的定义算法中我们需要进行n * n * n次乘法运算,新算法中我们需要进行7log2n次乘法,对于最常用的4阶矩阵: 原算法 新算法
加法次数 48 72(48次加法,24次减法)
乘法次数 64 49
需要额外空间 16 * sizeof(float) 28 * sizeof(float)
新算法要比原算法多了24次减法运算,少了15次乘法。但因为浮点乘法的运算速度要远远慢于加/减法运算,所以新算法的整体速度有所提高。
加载全部内容