Python KMP 浅谈Python描述数据结构之KMP篇
夏悠然然 人气:0前言
本篇章主要介绍串的KMP模式匹配算法及其改进,并用Python实现KMP算法。
1. BF算法
BF算法,即
假设主串
def BF(substrS, substrT):
if len(substrT) > len(substrS):
return -1
j = 0
t = 0
while j < len(substrS) and t < len(substrT):
if substrT[t] == substrS[j]:
j += 1
t += 1
else:
j = j - t + 1
t = 0
if t == len(substrT):
return j - t
else:
return -1
2. KMP算法
KMP算法,是由
就是这次匹配失败时,下次匹配时模式串应该从哪一位开始比较。
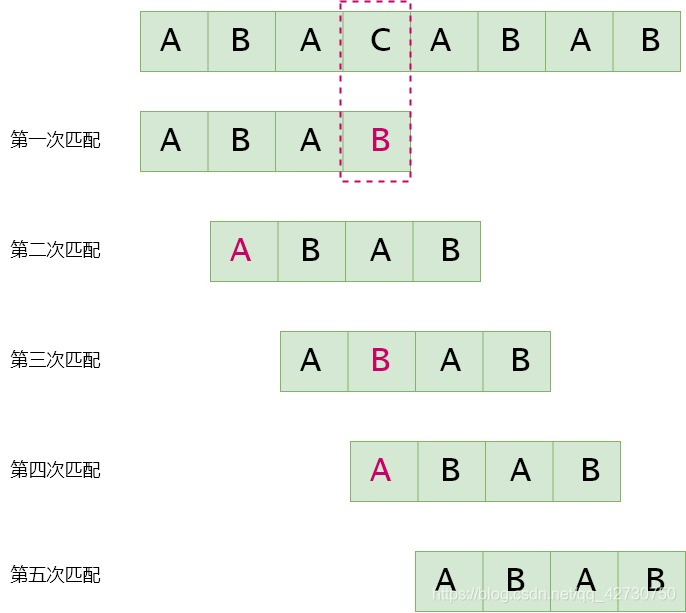
BF算法思路简单,便于理解,但是在执行时效率太低。在上述的匹配过程中,第一次匹配时已经匹配的
前缀:是指除最后一个字符外,字符串的所有头部子串。
后缀:是指除第一个字符外,字符串的所有尾部子串。
部分匹配值
例如,
前缀一定包含第一个字符,后缀一定包含最后一个字符。

如果模式串1号位与主串当前位(箭头所指的位置)不匹配,将模式串1号位与主串的下一位进行比较。next[0]=-1,这边就是一个特殊位置了,即如果主串与模式串的第1位不相同,那么下次就直接比较各第2位的字符。
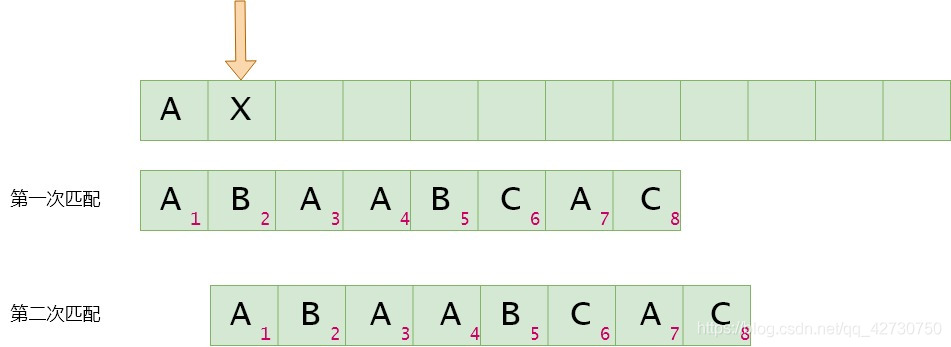
如果模式串2号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为

如果模式串3号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为
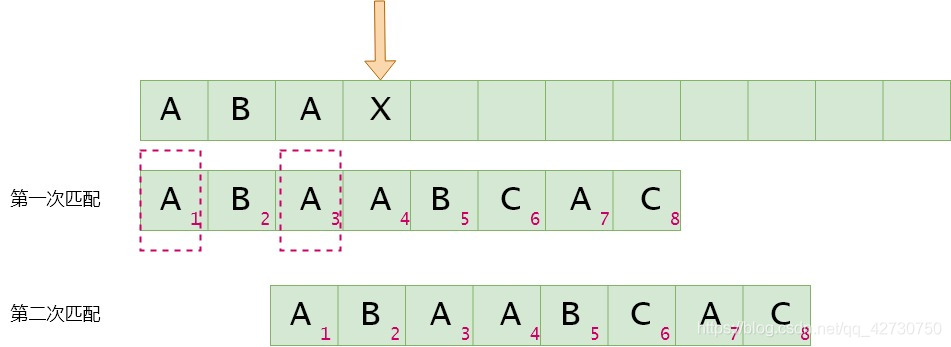
如果模式串4号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为

如果模式串5号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为
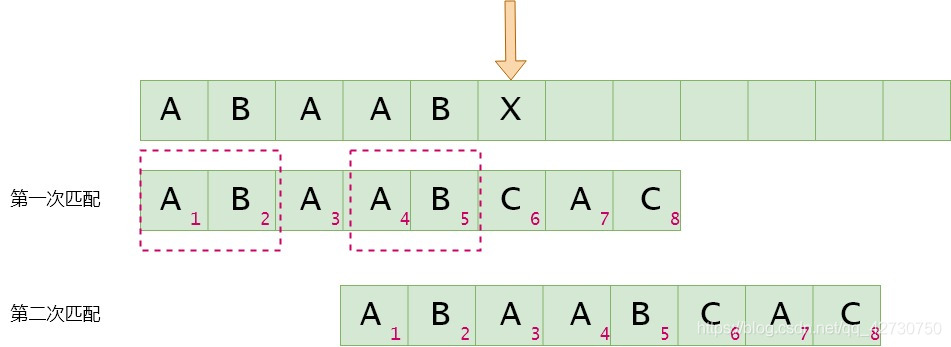
如果模式串6号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为
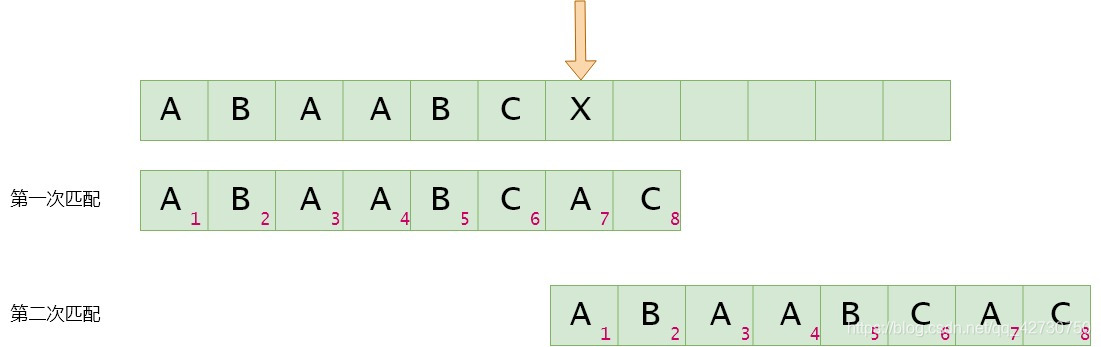
如果模式串7号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为

如果模式串8号位与主串当前位不匹配,找最长公共前后缀,指针前面的子串为
综上,可以得到模式串的next数组,发现没有,把主串去掉也可以得到这个数组,即下次匹配时模式串向后移动的位数与主串无关,仅与模式串本身有关。
| 位编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 索引 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 模式串 | A | B | A | A | B | C | A | C |
| next | -1 | 0 | 0 | 1 | 1 | 2 | 0 | 1 |
next数组,即存放的是每个字符匹配失败时,对应的下一次匹配时模式串开始匹配的位置。
如何在代码里实现上述流程呢?举个栗子,蓝色方框圈出的就是公共前后缀,假设next[j]=t:

当
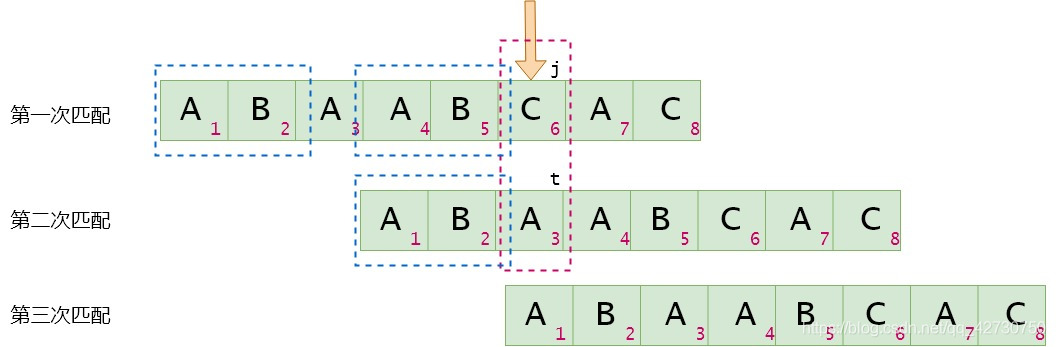
当
代码如下:
def getNext(substrT):
next_list = [-1 for i in range(len(substrT))]
j = 0
t = -1
while j < len(substrT) - 1:
if t == -1 or substrT[j] == substrT[t]:
j += 1
t += 1
# Tj=Tt, 则可以到的next[j+1]=t+1
next_list[j] = t
else:
# Tj!=Tt, 模式串T索引为t的字符与当前位进行匹配
t = next_list[t]
return next_list
def KMP(substrS, substrT, next_list):
count = 0
j = 0
t = 0
while j < len(substrS) and t < len(substrT):
if substrS[j] == substrT[t] or t == -1:
# t == -1目的就是第一位匹配失败时
# 主串位置加1, 匹配串回到第一个位置(索引为0)
# 匹配成功, 主串和模式串指针都后移一位
j += 1
t += 1
else:
# 匹配失败, 模式串索引为t的字符与当前位进行比较
count += 1
t = next_list[t]
if t == len(substrT):
# 这里返回的是索引
return j - t, count+1
else:
return -1, count+1
3. KMP算法优化版
上面定义的next数组在某些情况下还有些缺陷,发现没有,在第一个图中,我们还可以跳过第3次匹配,直接进行第4次匹配。为了更好地说明问题,我们以下面这种情况为例,来优化一下KMP算法。假设主串

可以看到第2、3、4次的匹配是多余的,因为我们在第一次匹配时,主串
那么,问题出在哪里???我们结合着next数组看一下:
| 位编号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 索引 | 0 | 1 | 2 | 3 | 4 |
| 模式串 | A | A | A | A | B |
| next | -1 | 0 | 1 | 2 | 3 |
问题在于,当
所以,我们要修正一下next数组。
大致流程和上面求解next数组时一样,这里就是多了一个判别条件,如果在匹配时出现了
代码如下:
def getNextval(substrT):
nextval_list = [-1 for i in range(len(substrT))]
j = 0
t = -1
while j < len(substrT) - 1:
if t == -1 or substrT[j] == substrT[t]:
j += 1
t += 1
if substrT[j] != substrT[t]:
# Tj=Tt, 但T(j+1)!=T(t+1), 这个就和next数组计算时是一样的
# 可以得到nextval[j+1]=t+1
nextval_list[j] = t
else:
# Tj=Tt, 且T(j+1)==T(t+1), 这个就是next数组需要更新的
# nextval[j+1]=上一次的nextval_list[t]
nextval_list[j] = nextval_list[t]
else:
# 匹配失败, 模式串索引为t的字符与当前位进行比较
t = nextval_list[t]
return nextval_list
对KMP的优化其实就是对next数组的优化,修正后的next数组,即nextval数组如下:
| 位编号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 索引 | 0 | 1 | 2 | 3 | 4 |
| 模式串 | A | A | A | A | B |
| nextval | -1 | -1 | -1 | -1 | 3 |
下面就测试一下:
if __name__ == '__main__':
S1 = 'ABACABAB'
T1 = 'ABAB'
S2 = 'AAABAAAAB'
T2 = 'AAAAB'
print('*' * 50)
print('主串S={0}与模式串T={1}进行匹配'.format(S1, T1))
print('{:*^25}'.format('KMP'))
next_list1 = getNext(T1)
print('next数组为: {}'.format(next_list1))
index1_1, count1_1 = KMP(S1, T1, next_list1)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index1_1, count1_1))
print('{:*^25}'.format('KMP优化版'))
nextval_list1 = getNextval(T1)
print('nextval数组为: {}'.format(nextval_list1))
index1_2, count1_2 = KMP(S1, T1, nextval_list1)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index1_2, count1_2))
print('')
print('*' * 50)
print('主串S={0}与模式串T={1}进行匹配'.format(S2, T2))
print('{:*^25}'.format('KMP'))
next_list2 = getNext(T2)
print('next数组为: {}'.format(next_list2))
index2_1, count2_1 = KMP(S2, T2, next_list2)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index2_1, count2_1))
print('{:*^25}'.format('KMP优化版'))
nextval_list2 = getNextval(T2)
print('nextval数组为: {}'.format(nextval_list2))
index2_2, count2_2 = KMP(S2, T2, nextval_list2)
print('匹配到的位置(索引): {}, 匹配次数: {}'.format(index2_2, count2_2))
运行结果如下:
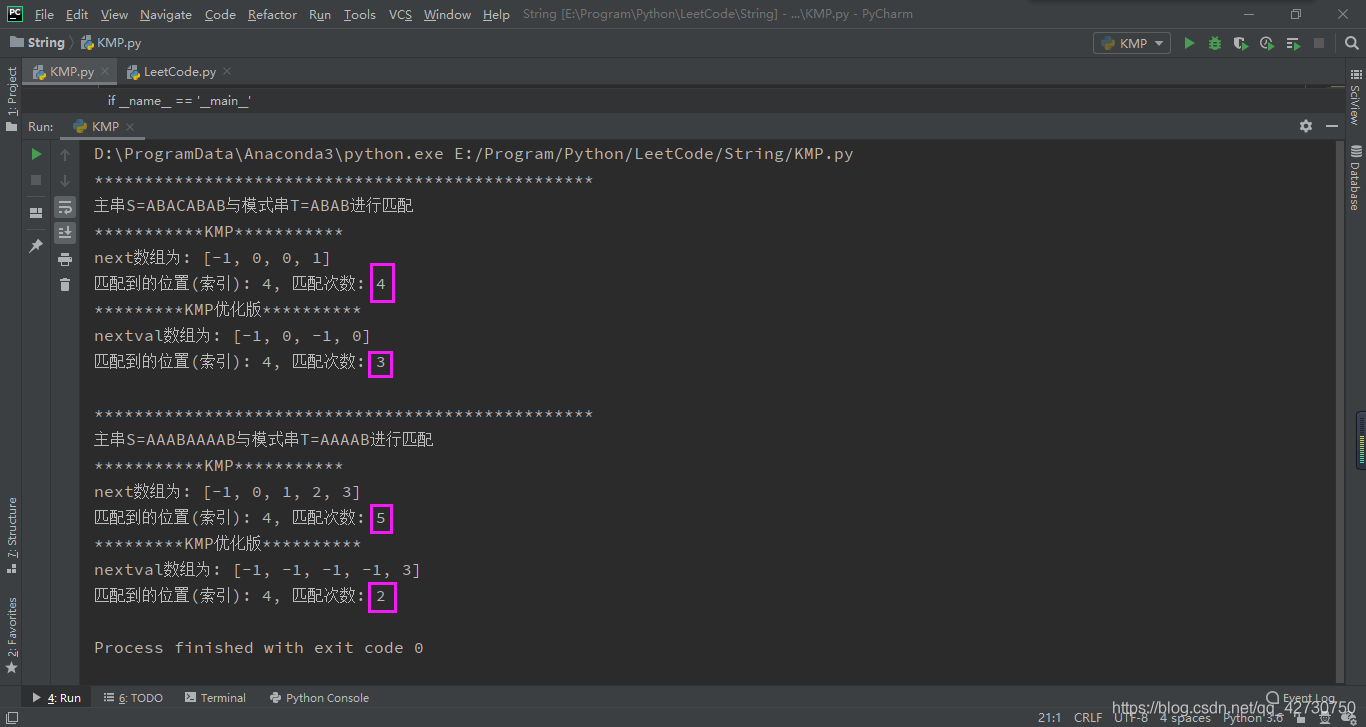
运行的结果和我们分析的是一样的,不修正next数组时,主串
结束语
在写本篇博客之前也是反复看参考书、视频,边画图边去理解它,这篇博客也是反复修改了好几次,最终算是把KMP解决掉了,有关字符串知识的复习也算是基本结束,下面就是刷题了(虽然在LeetCode做过了几道题)。
加载全部内容